NCERT Solutions for Class 10 Maths Chapter 11 - Areas Related to Circles (Exercise 12.3)
NCERT TEXTBOOK QUESTIONS SOLVED
Page No. 234
EXERCISE 12.3
Unless stated otherwise, use π = 22/7
Q 1. Find the area of the shaded region in Fig. PQ = 24 cm, PR = 7 cm and O is the centre of the circle.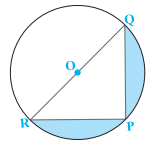
Sol. Since O is the centre of the circle,
∴ QOR is a diameter.
⇒ ∠RPQ = 90° [Angle in a semi-circle]
Now, in right ∆ RPQ,
RQ2 = PQ2 + PR2
⇒ RQ2 = 242 + 72 = 576 + 49 = 625
⇒ RQ
∴ Area of Δ RPQ
Now, area of semi-circle
∴ Area of the shaded portion = 245.54 cm2 − 84 cm2 = 161.54 cm2.
Page No. 235
Q 2. Find the area of the shaded region in figures, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.
Sol. Radius of the outer circle = 14 cm
Here, θ = 40°
∴ Area of the sector
Radius of the inner circle = 7 cm
Here, also θ = 40°
∴ Area of the sector BOD
Now, area of the shaded region = [Area of sector AOC] − [Area of sector BOD]
Q 3. Find the area of the shaded region in figure, if ABCD is a square of side 14 cm and APD and BPC are semi-circles.
Sol. Side of the square = 14 cm
∴ Area of the square ABCD=14 × 14 cm2 = 196 cm2
Now, diameter of the circle = (Side of the square) = 14 cm
⇒ Radius of each of the circles = 14/2 = 7cm
∴ Area of the semi-circle
Area of the semi-circle BPC
∴ Area the shaded region = [Area of the square] − [Area of semicircle APD + Area of semicircle BPC]
= 196 − [77 + 77] cm2 = 196 − 154 cm2 = 42 cm2.
Q 4. Find the area of the shaded region in figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
Sol. Area of the circle with radius = 6 cm.
Area of equilateral triangle, having side a = 12 cm, is given by
∵ Each angle of an equilateral triangle = 60°
∠AOB = 60°
∴ Area of sector COD
Now, area of the shaded region, = [Area of the circle] + [Area of the equilateral triangle] − [Area of the sector COD]
Q 5. From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in figure. Find the area of the remaining portion of the square.
Sol. Side of the square = 4 cm
∴ Area of the square ABCD = 4 × 4 cm2 = 16 cm2
∵ Each corner has a quadrant circle of radius 1 cm.
∴ Area of all the 4 quadrant squares
Diameter of the middle circle = 2 cm
⇒ Radius of the middle circle = 1 cm
∴ Area of the middle circle = πr2
Now, area of the shaded region = [Area of the square ABCD] − [(Area of the 4 quadrant circles) + (Area of the middle circle)]
Q 6. In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in figure. Find the area of the design.
Sol. Area of the circle having radius r = 32 cm.
= πr2
‘O’ is the centre of the circle,
∴ AO = OB = OC = 32 cm
⇒ ∠AOB = ∠BOC = ∠AOC = 120°
Now, in Δ AOB, ∠1 = 30°
∵ ∠1 + ∠2 = 60°
Also OA = OB ⇒∠1 = ∠2
If OM ⊥ AB, then
⇒
Also,
⇒
⇒
Now, area of Δ AOB, =
Since area Δ ABC = 3 × [area of ∆ AOB] =
Now, area of the design = [Area of the circle] − [Area of the equilateral triangle]
Page No. 236
Q 7. In figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Sol. Side of the square ABCD = 14 cm
∴ Area of the square ABCD = 14 × 14 cm2 = 196 cm2.
∵ Circles touch each other
∴ Radius of a circle = 14/2 = 7 cm
Now, area of a sector of radius 7 cm and sector angle θ as 90°
⇒ Area of 4 sectors =
∴ Area of the shaded region = [Area of the square ABCD] − [Area of the 4 sectors]
= 196 cm2 − 154 cm2 = 42 cm2.
Q 8. The figure depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m long.
If the track is 10 m wide, find:
(i) the distance around the track along its inner edge
(ii) the area of the track.
Sol. (i) Distance around the track along its inner edge
(ii) Now, area of the track
= Area of the shaded region = (Area of rectangle ABCD) + (Area of rectangle EFGH) [ The track is 10 m wide]
⇒ Area of the track
= (106 × 10 m2) + (106 × 10 m2) = 2120 m2 + 2200 m2 = 4320 m2.
Q 9. In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Sol. O is the centre of the circle.
OA =7 cm
⇒ AB = 2 OA = 2 × 7 = 14 cm
OC = OA = 7 cm
∵ AB and CD are perpendicular to each other
⇒ OC ⊥ AB
∴ Area Δ ABC
Again OD = OA = 7 cm
∴ Radius of the small circle
∴ Area of the small circle
Radius of the big circle 14/2 cm = 7 cm
∴ Area of semi-circle OABC
= 11 × 7 cm2 = 77 cm2
Now, Area of the shaded region = [Area of the small circle] + [Area of the big semi-circle OABC] − [Area of Δ ABC]
Q 10. The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig.). Find the area of the shaded region.
(Use π = 3.14 and √3 = 1.73205).
Sol. Area of ∆ ABC = 17320.5 cm2
∵ Δ ABC is an equilateral triangle and area of an
⇒ Radius of each circle = 200/2 = 100 cm
Since each angle of an equilateral triangle is 60°,
∴∠A = ∠B = ∠C = 60°
∴ Area of a sector having angle of sector as 60° and radius 100 cm.
∴ Area of 3 equal sectors
Now, area of the shaded region = [Area of the equilateral triangle ABC] − [Area of 3 equal sectors]
= 17320.5 cm2 − 15700 cm2 = 1620.5 cm2.
Page No. 237
Q 11. On a square handkerchief, nine circular designs each of radius 7 cm are made (see figure). Find the area of the remaining portion of the handkerchief.
Sol. ∵ The circles touch each other.
∴ The side of the square ABCD
= 3 × diameter of a circle
= 3 × (2 × radius of a circle) = 3 × (2 × 7 cm)
= 42 cm
⇒ Area of the square ABCD = 42 × 42 cm2 = 1764 cm2.
Now, area of one circle =
∵ There are 9 squares
∴ Total area of 9 circles = 154 × 9 = 1386 cm2
∴ Area of the remaining portion of the handkerchief = 1764 − 1386 cm2 = 378 cm2.
Q 12. In the figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB, (ii) shaded region.
Sol. Here, centre of the circle is O and radius = 3.5 cm.
∴ Area of the quadrant [∵ OB = 3.5 cm = radius and OD = 2 cm (given)]
∴ Area of the shaded region
= (Area of the quadrant OACB) − (Area of ∆ BOD)
Q 13. In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
Sol. Given: side of the square OABC = OA = 20 cm .
∴ Area of the square = 20 x 20 = 400 cm2
Diagonal of the square =√2 x (side of the square)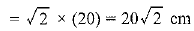
Radius of the quadrant of circle = Diagonal of square = 20√2 cm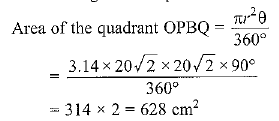
Area of the shaded region = Area of the quadrant - Area of the square
=628 - 400 = 228 cm2
Q 14. AB and CD are respectively areas of two concentric circles of radii 21 cm and 7 cm and centre O (see figure). If ∠AOB = 30°, find the area of the shaded region.
Sol. ∵ Radius of bigger circle
R = 21 cm
and sector angle θ = 30°
∴ Area of the sector OAB
Again, radius of the smaller circle r =7 cm
Here also, the sector angle is 30°
∴ Area of the sector OCD
∴ Area of the shaded region
Q 15. In the figure, ABPC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
Sol. Radius of the quadrant = 14 cm
Therefore, area of the quadrant ABPC
Area of right
⇒ Area of segment BPC = 154 cm2 − 98 cm2 = 56 cm2
Now, in right Δ ABC,
AC2 + AB2 = BC2
⇒ 142 + 142 = BC2
⇒ 196 + 196 = BC2
⇒ BC2 = 392 ⇒ BC = 14√2cm .
∴ Radius of the semi-circle BQC
∴ Area of the semi-circle BQC
Now, area of the shaded region = [Area of segment BQC] − [Area of segment BPC]
= 154 cm2 − 56 cm2 = 98 cm2.
Page No. 238
Q 16. Calculate the area of the designed region in the figure, common between the two quadrants of circles of radius 8 cm each.
Sol. ∵ Side of the square = 8 cm
∴ Area of the square (ABCD) = 8 × 8 cm2
= 64 cm2
Now, radius of the quadrant ADQB = 8 cm
∴ Area of the quadrant ADQB
Similarly, area of the quadrant BPDC
∴ Sum of the two quadrants
Now, area of design = [Sum of the areas of the two quadrants] − [Area of the square ABCD]
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 11 - Areas Related to Circles (Exercise 12.3)
| 1. What is the formula to find the area of a circle? |  |
| 2. How is the circumference of a circle related to its radius? |  |
| 3. Can the area of a circle be negative? |  |
| 4. How can the area of a sector of a circle be calculated? |  |
| 5. Can the radius of a circle be a negative value? |  |

















