NCERT Solutions for Class 10 Maths Chapter 6 - Triangles (Exercise 6.1)
Exercise 6.1
Q1: Fill in the blanks using the correct word given in brackets.
(i) All circles are _______(congruent, similar).
(ii) All squares are _______ (similar, congruent).
(iii) All _______ triangles are similar. (isosceles, equilateral).
(iv)Two polygons of the same number of sides are similar, if (a) their corresponding angles are _______ and (b) their corresponding sides are _______ (equal, proportional).
Ans:
(i) All circles are similar.
(ii) All squares are similar.
(iii) All equilateral triangles are similar.
(iv) Two polygons of the same number of sides are similar if:
(a) Their corresponding angles are equal and
(b) Their corresponding sides are proportional.
Q2: Give two different examples of pair of:
(i) similar figures
(ii) non-similar figures.
Ans:
(i).
(a) Any two circles are similar figures.
(b) Any two squares are similar figures.
(ii).
(a) A circle and a triangle are non-similar figures.
(b) An isosceles triangle and a scalene triangle are non-similar figures.
Q3: State whether the following quadrilaterals are similar or not.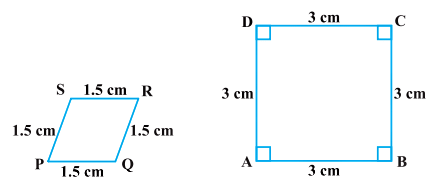
Ans: No, the sides of quadrilateral PQRS and ABCD are proportional but their corresponding angles are not equal.
∴ These are not similar.
Exercise 6.2
Q1. In figures (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
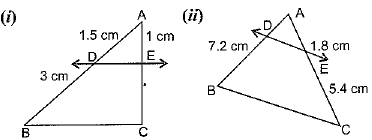
Sol.
(i) Given, in △ ABC, DE∥BC
∴ AD/DB = AE/EC [Using Basic proportionality theorem]
⇒ 1.5/3 = 1/EC
⇒ EC = 3/1.5
EC = 3×10/15 = 2 cm
Hence, EC = 2 cm.
(ii) Given, in △ ABC, DE∥BC
∴ AD/DB = AE/EC [Using Basic proportionality theorem]
⇒ AD/7.2 = 1.8 / 5.4
⇒ AD = 1.8 ×7.2/5.4 = (18/10)×(72/10)×(10/54) = 24/10
⇒ AD = 2.4
Hence, AD = 2.4 cm.
Q2. E and F are points on the sides PQ and PR respectively of a ΔPQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Sol.
Given, in ΔPQR, E and F are two points on side PQ and PR respectively. See the figure below;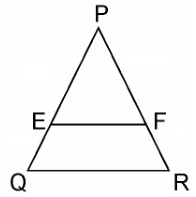
(i) Given, PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2,4 cm
Therefore, by using Basic proportionality theorem, we get,
PE/EQ = 3.9/3 = 39/30 = 13/10 = 1.3
And PF/FR = 3.6/2.4 = 36/24 = 3/2 = 1.5
So, we get, PE/EQ ≠ PF/FR
Hence, EF is not parallel to QR.
(ii) Given, PE = 4 cm, QE = 4.5 cm, PF = 8cm and RF = 9cm
Therefore, by using Basic proportionality theorem, we get,
PE/QE = 4/4.5 = 40/45 = 8/9
And, PF/RF = 8/9
So, we get here,
PE/QE = PF/RF
Hence, EF is parallel to QR.
(iii) Given, PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
From the figure,
EQ = PQ – PE = 1.28 – 0.18 = 1.10 cm
And, FR = PR – PF = 2.56 – 0.36 = 2.20 cm
So, PE/EQ = 0.18/1.10 = 18/110 = 9/55…………. (i)
And, PE/FR = 0.36/2.20 = 36/220 = 9/55………… (ii)
So, we get here,
PE/EQ = PF/FR
Hence, EF is parallel to QR.
Q3.In the figure, if LM || CB and LN || CD, prove that
AM/AB = AN/AD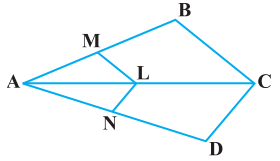 Sol.
Sol.
In the given figure, we can see, LM || CB,
By using basic proportionality theorem, we get,
AM/AB = AL/AC……………………..(i)
Similarly, given, LN || CD and using basic proportionality theorem,
∴ AN/AD = AL/AC……………………………(ii)
From equation (i) and (ii), we get,
AM/AB = AN/AD
Hence, proved.
Q4. In the figure, DE||AC and DF||AE. Prove that BF/FE = BE/EC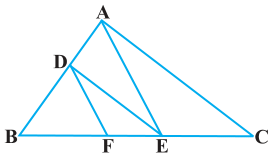 Sol.
Sol.
In ΔABC, given as, DE || AC
Thus, by using Basic Proportionality Theorem, we get,
∴ BD/DA = BE/EC ………………………………………………(i)
In ΔABC, given as, DF || AE
Thus, by using Basic Proportionality Theorem, we get,
∴ BD/DA = BF/FE ………………………………………………(ii)
From equation (i) and (ii), we get
BE/EC = BF/FE
Hence, proved.
Q5. In the figure, DE || OQ and DF || OR. Show that EF || QR.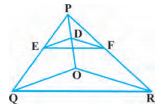 Sol.
Sol.
Given,
In ΔPQO, DE || OQ
So by using Basic Proportionality Theorem,
PD/DO = PE/EQ……………… ..(i)
Again given, in ΔPQO, DE || OQ ,
So by using Basic Proportionality Theorem,
PD/DO = PF/FR………………… (ii)
From equation (i) and (ii), we get,
PE/EQ = PF/FR
Therefore, by converse of Basic Proportionality Theorem,
EF || QR, in ΔPQR.
Q6. In the figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.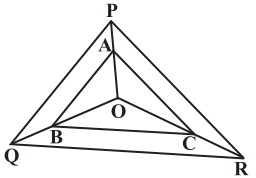 Sol.
Sol.
Given here,
In ΔOPQ, AB || PQ
By using Basic Proportionality Theorem,
OA/AP = OB/BQ…………….(i)
Also given,
In ΔOPR, AC || PR
By using Basic Proportionality Theorem
∴ OA/AP = OC/CR……………(ii)
From equation (i) and (ii), we get,
OB/BQ = OC/CR
Therefore, by converse of Basic Proportionality Theorem,
In ΔOQR, BC || QR.
Q7. Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. 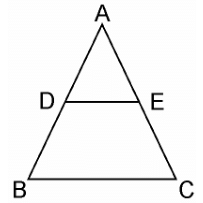 Sol.
Sol.
Given, in ΔABC, D is the midpoint of AB such that AD=DB.
A line parallel to BC intersects AC at E as shown in above figure such that DE || BC.
We have to prove that E is the mid point of AC.
Since, D is the mid-point of AB.
∴ AD=DB
⇒ AD/DB = 1 ………… (i)
In ΔABC, DE || BC,
By using Basic Proportionality Theorem,
Therefore, AD/DB = AE/EC
From equation (i), we can write,
⇒ 1 = AE/EC
∴ AE = EC
Hence, proved, E is the midpoint of AC.
Q8. Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Sol.
Given, in ΔABC, D and E are the mid points of AB and AC respectively, such that,
AD=BD and AE=EC. We have to prove that: DE || BC.
We have to prove that: DE || BC.
Since, D is the midpoint of AB
∴ AD=DB
⇒ AD/BD = 1…………. (i)
Also given, E is the mid-point of AC.
∴ AE=EC
⇒ AE/EC = 1
From equation (i) and (ii), we get,
AD/BD = AE/EC
By converse of Basic Proportionality Theorem,
DE || BC
Hence, proved.
Q9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that AO/BO = CO/DO.
Sol. Given, ABCD is a trapezium where AB || DC and diagonals AC and BD intersect each other at O.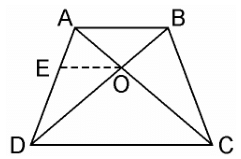
We have to prove, AO/BO = CO/DO
From the point O, draw a line EO touching AD at E, in such a way that,
EO || DC || AB
In ΔADC, we have OE || DC
Therefore, By using Basic Proportionality Theorem
AE/ED = AO/CO ……………..(i)
Now, In ΔABD, OE || AB
Therefore, By using Basic Proportionality Theorem
DE/EA = DO/BO…………….(ii)
From equation (i) and (ii), we get,
AO/CO = BO/DO
⇒ AO/BO = CO/DO
Hence, proved.
Q10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO = CO/DO. Show that ABCD is a trapezium.
Sol.
Given, Quadrilateral ABCD where AC and BD intersects each other at O such that,
AO/BO = CO/DO.
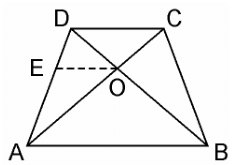 We have to prove here, ABCD is a trapezium
We have to prove here, ABCD is a trapezium
From the point O, draw a line EO touching AD at E, in such a way that,
EO || DC || AB
In ΔDAB, EO || AB
Therefore, By using Basic Proportionality Theorem
DE/EA = DO/OB ………(i)
Also, given,
AO/BO = CO/DO
⇒ AO/CO = BO/DO
⇒ CO/AO = DO/BO
⇒ DO/OB = CO/AO ………….(ii)
From equation (i) and (ii), we get
DE/EA = CO/AO
Therefore, By using converse of Basic Proportionality Theorem,
EO || DC also EO || AB
⇒ AB || DC.
Hence, quadrilateral ABCD is a trapezium with AB || CD.
Exercise 6.3
Q1. State which pairs of triangles in Figure, are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

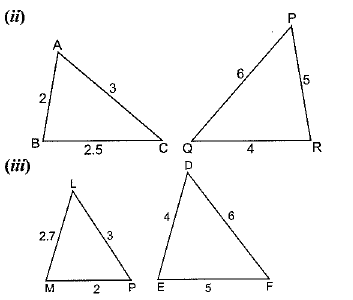
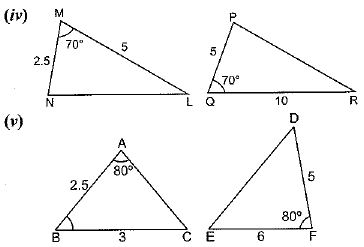
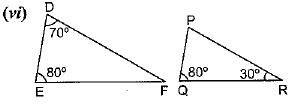
Sol.
(i) Given, in ΔABC and ΔPQR,
∠A = ∠P = 60°
∠B = ∠Q = 80°
∠C = ∠R = 40°
Therefore by AAA similarity criterion,
∴ ΔABC ~ ΔPQR
(ii) Given, in ΔABC and ΔPQR,
AB/QR = BC/RP = CA/PQ
By SSS similarity criterion,
ΔABC ~ ΔQRP
(iii) Given, in ΔLMP and ΔDEF,
LM = 2.7, MP = 2, LP = 3, EF = 5, DE = 4, DF = 6
MP/DE = 2/4 = 1/2
PL/DF = 3/6 = 1/2
LM/EF = 2.7/5 = 27/50
Here , MP/DE = PL/DF ≠ LM/EF
Therefore, ΔLMP and ΔDEF are not similar.
(iv) In ΔMNL and ΔQPR, it is given,
MN/QP = ML/QR = 1/2
∠M = ∠Q = 70°
Therefore, by SAS similarity criterion
∴ ΔMNL ~ ΔQPR
(v) In ΔABC and ΔDEF, given that,
AB = 2.5, BC = 3, ∠A = 80°, EF = 6, DF = 5, ∠F = 80°
Here , AB/DF = 2.5/5 = 1/2
And, BC/EF = 3/6 = 1/2
⇒ ∠B ≠ ∠F
Hence, ΔABC and ΔDEF are not similar.
(vi) In ΔDEF, by sum of angles of triangles, we know that,
∠D + ∠E + ∠F = 180°
⇒ 70° + 80° + ∠F = 180°
⇒ ∠F = 180° – 70° – 80°
⇒ ∠F = 30°
Similarly, In ΔPQR,
∠P + ∠Q + ∠R = 180 (Sum of angles of Δ)
⇒ ∠P + 80° + 30° = 180°
⇒ ∠P = 180° – 80° -30°
⇒ ∠P = 70°
Now, comparing both the triangles, ΔDEF and ΔPQR, we have
∠D = ∠P = 70°
∠F = ∠Q = 80°
∠F = ∠R = 30°
Therefore, by AAA similarity criterion,
Hence, ΔDEF ~ ΔPQR
Q2. In the figure, ΔODC ~ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
Sol.
As we can see from the figure, DOB is a straight line.
Therefore, ∠DOC + ∠ COB = 180°
⇒ ∠DOC = 180° – 125° (Given, ∠ BOC = 125°)
= 55°
In ΔDOC, sum of the measures of the angles of a triangle is 180º
Therefore, ∠DCO + ∠ CDO + ∠ DOC = 180°
⇒ ∠DCO + 70º + 55º = 180°(Given, ∠ CDO = 70°)
⇒ ∠DCO = 55°
It is given that, ΔODC ∝ ¼ ΔOBA,
Therefore, ΔODC ~ ΔOBA.
Hence, Corresponding angles are equal in similar triangles
∠OAB = ∠OCD
⇒ ∠ OAB = 55°
∠OAB = ∠OCD
⇒ ∠OAB = 55°
Q3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that AO/OC = OB/OD
Sol. 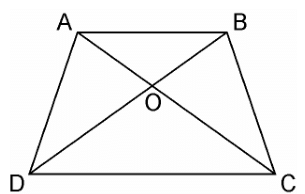
In ΔDOC and ΔBOA,
AB || CD, thus alternate interior angles will be equal,
∴ ∠CDO = ∠ABO
Similarly,
∠DCO = ∠BAO
Also, for the two triangles ΔDOC and ΔBOA, vertically opposite angles will be equal;
∴ ∠DOC = ∠BOA
Hence, by AAA similarity criterion,
ΔDOC ~ ΔBOA
Thus, the corresponding sides are proportional.
DO/BO = OC/OA
⇒ OA/OC = OB/OD
Hence, proved.
Q4. In the figure, QR/QS = QT/PR and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.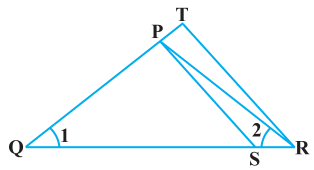 Sol.
Sol.
In ΔPQR,
∠PQR = ∠PRQ
∴ PQ = PR ……(i)
Given,
QR/QS = QT/PR Using equation (i), we get
QR/QS = QT/QP……….(ii)
In ΔPQS and ΔTQR, by equation (ii),
QR/QS = QT/QP
∠Q = ∠Q
∴ ΔPQS ~ ΔTQR [By SAS similarity criterion]
Q5. S and T are points on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ~ ΔRTS.
Sol.
Given, S and T are point on sides PR and QR of ΔPQR
And ∠P = ∠RTS.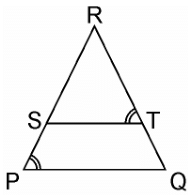 In ΔRPQ and ΔRTS,
In ΔRPQ and ΔRTS,
∠RTS = ∠QPS (Given)
∠R = ∠R (Common angle)
∴ ΔRPQ ~ ΔRTS (AA similarity criterion)
Q6. In the figure, if ΔABE ≌ ΔACD, show that ΔADE ~ ΔABC.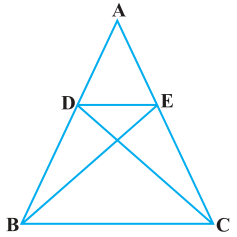 Sol.
Sol.
Given, ΔABE ≅ ΔACD.
∴ AB = AC [By CPCT] …………….(i)
And, AD = AE [By CPCT] ………(ii)
In ΔADE and ΔABC, dividing eq.(ii) by eq(i),
AD/AB = AE/AC
∠A = ∠A [Common angle]
∴ ΔADE ~ ΔABC [SAS similarity criterion]
Q7. In the figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that: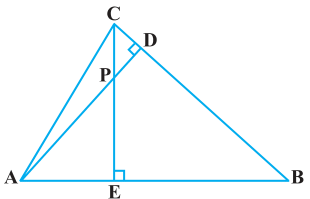
(i) ΔAEP ~ ΔCDP
(ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB
(iv) ΔPDC ~ ΔBEC
Sol.
Given, altitudes AD and CE of ΔABC intersect each other at the point P.
(i) In ΔAEP and ΔCDP,
∠AEP = ∠CDP (90° each)
∠APE = ∠CPD (Vertically opposite angles)
Hence, by AA similarity criterion,
ΔAEP ~ ΔCDP
(ii) In ΔABD and ΔCBE,
∠ADB = ∠CEB ( 90° each)
∠ABD = ∠CBE (Common Angles)
Hence, by AA similarity criterion,
ΔABD ~ ΔCBE
(iii) In ΔAEP and ΔADB,
∠AEP = ∠ADB (90° each)
∠PAE = ∠DAB (Common Angles)
Hence, by AA similarity criterion,
ΔAEP ~ ΔADB
(iv) In ΔPDC and ΔBEC,
∠PDC = ∠BEC (90° each)
∠PCD = ∠BCE (Common angles)
Hence, by AA similarity criterion,
ΔPDC ~ ΔBEC
Q8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that Δ ABE ~ ΔCFB.
Sol.
Given, E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Consider the figure below,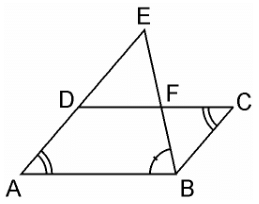
In ΔABE and ΔCFB,
∠A = ∠C (Opposite angles of a parallelogram)
∠AEB = ∠CBF (Alternate interior angles as AE || BC)
∴ ΔABE ~ ΔCFB (AA similarity criterion)
Q9. In the figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that: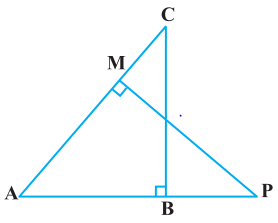 (i) Δ ABC ~ Δ AMP
(i) Δ ABC ~ Δ AMP
(ii) CA/PA = BC/MP
Sol.
Given, ABC and AMP are two right triangles, right angled at B and M respectively.
(i) In ΔABC and ΔAMP, we have,
∠CAB = ∠MAP (common angles)
∠ABC = ∠AMP = 90° (each 90°)
∴ ΔABC ~ ΔAMP (AA similarity criterion)
(ii) As, ΔABC ~ ΔAMP (AA similarity criterion)
If two triangles are similar then the corresponding sides are always equal,
Hence, CA/PA = BC/MP
Q10. CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of Δ ABC and Δ EFG respectively. If ΔABC ~ ΔFEG, show that:
(i) CD/GH = AC/FG
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
Sol. Given, CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively.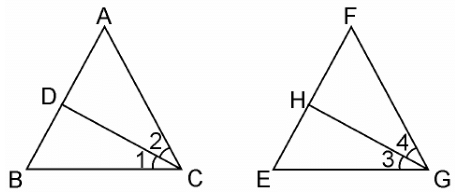
(i) From the given condition,
ΔABC ~ ΔFEG.
∴ ∠A = ∠F, ∠B = ∠E, and ∠ACB = ∠FGE
Since, ∠ACB = ∠FGE
∴ ∠ACD = ∠FGH (Angle bisector)
And, ∠DCB = ∠HGE (Angle bisector)
In ΔACD and ΔFGH,
∠A = ∠F
∠ACD = ∠FGH
∴ ΔACD ~ ΔFGH (AA similarity criterion)
⇒ CD/GH = AC/FG
(ii) In ΔDCB and ΔHGE,
∠DCB = ∠HGE (Already proved)
∠B = ∠E (Already proved)
∴ ΔDCB ~ ΔHGE (AA similarity criterion)
(iii) In ΔDCA and ΔHGF,
∠ACD = ∠FGH (Already proved)
∠A = ∠F (Already proved)
∴ ΔDCA ~ ΔHGF (AA similarity criterion)
Q11. In the figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥BC and EF ⊥AC, prove that ΔABD ~ ΔECF.
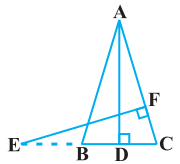 Sol.
Sol.
Given, ABC is an isosceles triangle.
∴ AB = AC
⇒ ∠ABD = ∠ECF
In ΔABD and ΔECF,
∠ADB = ∠EFC (Each 90°)
∠BAD = ∠CEF (Already proved)
∴ ΔABD ~ ΔECF (using AA similarity criterion)
Q12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of Δ PQR (see figure). Show that Δ ABC ~ ΔPQR.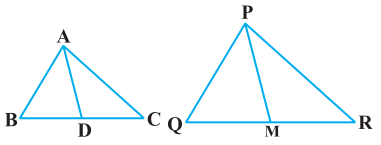 Sol.
Sol.
Given, ΔABC and ΔPQR, AB, BC and median AD of ΔABC are proportional to sides PQ, QR and median PM of ΔPQR
i.e. AB/PQ = BC/QR = AD/PM
We have to prove: ΔABC ~ ΔPQR
As we know here,
AB/PQ = BC/QR = AD/PM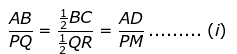
⇒ AB/PQ = BC/QR = AD/PM (D is the midpoint of BC. M is the midpoint of QR)
⇒ ΔABD ~ ΔPQM [SSS similarity criterion]
∴ ∠ABD = ∠PQM [Corresponding angles of two similar triangles are equal]
⇒ ∠ABC = ∠PQR
In ΔABC and ΔPQR
AB/PQ = BC/QR ………………………….(i)
∠ABC = ∠PQR ……………………………(ii)
From equation (i) and (ii), we get,
ΔABC ~ ΔPQR [SAS similarity criterion]
Q13. D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD.
Sol.
Given, D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC.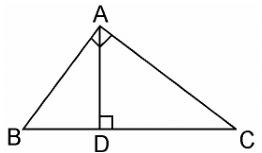
In ΔADC and ΔBAC,
∠ADC = ∠BAC (Already given)
∠ACD = ∠BCA (Common angles)
∴ ΔADC ~ ΔBAC (AA similarity criterion)
We know that corresponding sides of similar triangles are in proportion.
∴ CA/CB = CD/CA
⇒ CA2 = CB.CD.
Hence, proved.
Q14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
Sol.
Given: Two triangles ΔABC and ΔPQR in which AD and PM are medians such that;
AB/PQ = AC/PR = AD/PM
We have to prove, ΔABC ~ ΔPQR
Let us construct first: Produce AD to E so that AD = DE. Join CE, Similarly produce PM to
N such that PM = MN, also Join RN.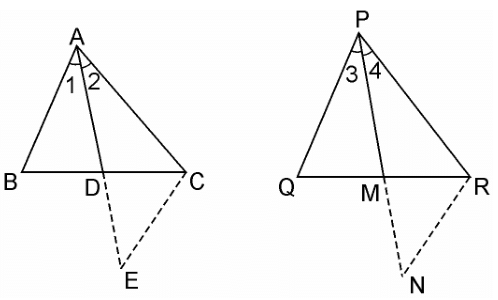 In ΔABD and ΔCDE, we have
In ΔABD and ΔCDE, we have
AD = DE [By Construction.]
BD = DC [Since, AP is the median]
and, ∠ADB = ∠CDE [Vertically opposite angles]
∴ ΔABD ≅ ΔCDE [SAS criterion of congruence]
⇒ AB = CE [By CPCT] …………………………..(i)
Also, in ΔPQM and ΔMNR,
PM = MN [By Construction.]
QM = MR [Since, PM is the median]
and, ∠PMQ = ∠NMR [Vertically opposite angles]
∴ ΔPQM = ΔMNR [SAS criterion of congruence]
⇒ PQ = RN [CPCT] ……………(ii)
Now, AB/PQ = AC/PR = AD/PM
From equation (i) and (ii),
⇒ CE/RN = AC/PR = AD/PM
⇒ CE/RN = AC/PR = 2AD/2PM
⇒ CE/RN = AC/PR = AE/PN [Since 2AD = AE and 2PM = PN]
∴ ΔACE ~ ΔPRN [SSS similarity criterion]
Therefore, ∠2 = ∠4
Similarly, ∠1 = ∠3
∴ ∠1 + ∠2 = ∠3 + ∠4
⇒ ∠A = ∠P …………….(iii)
Now, in ΔABC and ΔPQR, we have
AB/PQ = AC/PR (Already given)
From equation (iii),
∠A = ∠P
∴ ΔABC ~ ΔPQR [ SAS similarity criterion]
Q15. A vertical pole of length 6 cm casts a shadow 4 cm long on the ground and at the same time a tower casts a shadow 28 cm long. Find the height of the tower.
Sol.
Given, Length of the vertical pole = 6cm
Shadow of the pole = 4 cm
Let the Height of the tower = h cm
Length of shadow of the tower = 28 cm
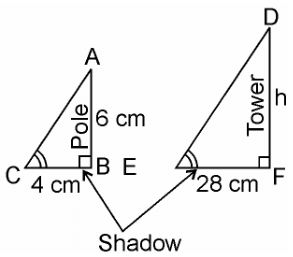
In ΔABC and ΔDEF,
∠C = ∠E (angular elevation of sum)
∠B = ∠F = 90°
∴ ΔABC ~ ΔDEF (AA similarity criterion)
∴ AB/DF = BC/EF (If two triangles are similar corresponding sides are proportional)
∴ 6/h = 4/28
⇒ h = (6×28)/4
⇒ h = 6 × 7
⇒ h = 42 cm
Hence, the height of the tower is 42 cm.
Q16. If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that AB/PQ = AD/PM..
Sol.
Given, ΔABC ~ ΔPQR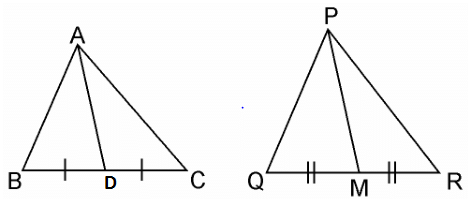 We know that the corresponding sides of similar triangles are in proportion.
We know that the corresponding sides of similar triangles are in proportion.
∴ AB/PQ = AC/PR = BC/QR……………………………(i)
Also, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ………….…..(ii)
Since AD and PM are medians, they will divide their opposite sides.
∴ BD = BC/2 and QM = QR/2 ……………..………….(iii)
From equations (i) and (iii), we get
AB/PQ = BD/QM ……………………….(iv)
In ΔABD and ΔPQM,
From equation (ii), we have
∠B = ∠Q
From equation (iv), we have,
AB/PQ = BD/QM
∴ ΔABD ~ ΔPQM (SAS similarity criterion)
⇒ AB/PQ = BD/QM = AD/PM
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 6 - Triangles (Exercise 6.1)
| 1. What are the properties of a triangle? |  |
| 2. How can we classify triangles based on their sides? |  |
| 3. How can we classify triangles based on their angles? |  |
| 4. How do we find the area of a triangle? |  |
| 5. How do we determine if three given side lengths can form a triangle? |  |






















