Theory & Procedure, Young Modulus | Additional Study Material for NEET PDF Download
Our Objective
Our aim is to determine the Young’s modulus of elasticity of the material of a given wire using Searle’s apparatus.
The Theory
Before we move ahead, do you know what a Searle’s apparatus is?
Searle’s apparatus consists of two metal frames F1 and F2. Each frame has a torsion head at the upper side and a hook at the lower side. These frames are suspended from two wires AB and CD of same material, length and cross-section. The upper ends of the wires are screwed tightly in two torsion heads fixed in the same rigid support. A spirit level rests horizontally with one end hinged in the frame F2. The other end of the spirit level rests on the tip of a spherometer screw, fitted in the frame F1. The spherometer screw can be rotated up and down along a vertical pitch scale marked in millimeters. The two frames are kept together by cross bars E1 and E2.
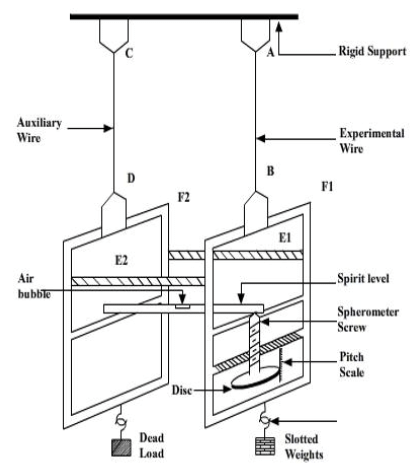
Do you know Searle’s apparatus works on the principle of Hooke’s law?
Hooke’s law can be expressed in terms of stress and strain. Stress is the force on a unit area within a material that develops as a result of the externally applied force. Strain is the relative deformation produced by stress.
Define Hooke’s Law
Hooke’s Law states that within the limit of elasticity, stress applied is directly proportional to strain produced. That is, the extension produced in a wire is directly proportional to the load attached to it.
If a wire of length L and radius r be loaded by a weight Mg and if l is the extension produced,
Then, normal stress = 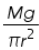 ---------------(1)
---------------(1)
And Longitudinal strain= 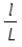 -----------------(2)
-----------------(2)
Hence, Young’s modulus
Where,
L – Length of the wire
l - Extension for a load M
r - Radius of the wire
g - Acceleration due to gravity
M - Mass added in the hanger
Now, let’s learn how to determine Young’s modulus using Searle’s apparatus .
Materials Required
- Searle’s apparatus
- Two long steel wires of same length and diameter
- A metre scale
- A set of 1/2 Kg slotted weights
- 1 Kg weight hanger
- 1 Kg dead load.
The Procedure
- Two wires of the same material, length and diameter have their ends tightened in torsion screws A,B, C and D as shown in Fig.
- Wire AB becomes the experimental wire and CD becomes the auxiliary wire.
- Suspend a 1 kg dead load from hook of frames F1 and F2.
- The weight hanger at F1 is loaded and unloaded 3 or 4 times, so that the experimental wire AB comes under elastic mood.
- Now, each wire has been loaded equally with 1 kg. The pitch and the least count of the spherometer are determined.
- The central screw is adjusted in such a way that the air bubble in the spirit level is exactly at the centre. The head scale reading of the spherometer is noted for zero weight in the weight hanger attached to the frame F1.
- A half kg of weight is now added to the weight hanger attached to the frame F1.
- The air bubble moves away from the centre. The spherometer screw is adjusted so that the air bubble comes back to the centre. The spherometer reading is noted.
- The load is increased in steps of half kg (maximum load should be less than the breaking stress) and the corresponding spherometer reading is noted.
- The same procedure is repeated for unloading the weights in steps of half kg. From these observations the extension, l for a load M can be determined.
- Young’s modulus can be calculated using the equation (3)
Simulator Procedure (as performed through the Online Labs)
- Select the environment from the drop down list.
- Select the material of the wire from the drop down list.
- Change the radius of the wire using the slider.
- Change the length of the wire using the slider.
- Change the weight in the weight hanger using the slider.
- Once the weight has been added to the weight hanger, the bubble in the sprit level moved to its extreme end.
- Click on the right/left arrow button on the bottom right side to move the spherometer upward/downward to adjust the bubble to the center.
- Note down the number of rotations and fractional rotations from the spherometer and the value from the scale.
- Calculate the extension, l, of the wire form the values.
- Calculate the Young’s modulus of the wire using the formula, Y = MgL/πr2l .
- To verify your result click on the ‘Show result’ check box.
- To redo the experiment, click on the ‘Reset’ button.
Our Observations:
To find the diameter of the wire using a screw gauge.
Distance moved by the screw for 4 rotations, x =………mm
Pitch of the screw, P =…………… mm
Number of divisions on the circular scale, N=.................
Least Count (L.C) of the screw gauge = =……………………….mm
Zero Correction, z =………………………..dvs
Slno | PSR(mm) | HSR(div) | Corrected HSR=HSR+z(div) | Total Reading=(PSR+(corrected HSR   L.C))mm L.C))mm |
Mean Diameter, d |
| |||
Radius of the experimental wire, r = d/2 =.............mm = ……x 10-3m
Length of the experimental wire, L =………..cm =…………x10 -2m
How to find Load and Extension
Least count of Spherometer
1 pitch scale division = 1mm
Number of full rotations given to screw = 4
|
26 videos|312 docs|64 tests
|
FAQs on Theory & Procedure, Young Modulus - Additional Study Material for NEET
| 1. What is the theory behind Young's Modulus? |  |
| 2. How is the Young's Modulus calculated? |  |
| 3. What is the significance of Young's Modulus in materials testing? |  |
| 4. How is the Young's Modulus experimentally determined? |  |
| 5. What are some practical applications of Young's Modulus? |  |

















