Some Basic Concepts in Chemistry Class 11 Notes Chemistry
What is the Matter?
Anything that has mass and occupies space is called matter.

The following are the characteristics of the matter:
- Particles have space between them
- Particles are continuously moving
- Particles attract each other
Classification of Matter
Based on the chemical composition of various substances matter is classified as Pure Substances & Mixtures.
 Classification of Matter
Classification of Matter
What is Pure Substance?
Pure substances are substances that are made up of only one kind of particles and has a fixed or constant structure.
Types of Pure Substances
Pure substances are further classified as elements and compounds.
1. Elements
- It is the simplest form of the matter.
- The smallest unit of an element is known as an atom.
- The total number of known elements is 118 out of which 98 elements occur naturally and 20 are formed by artificial transmutation.
- Examples: Na, K, Mg. Al, Si, P, C, F, Br etc.
2. Compound
- It is a non-elemental pure compound.
- Formed by the chemical combination of two or more atoms of different elements in a fixed ratio.
- Examples: H2O, CO2, C6H12O6 etc.
Characteristics & Properties Of Pure Substances
- Pure substances are mostly homogeneous in nature containing only one type of atoms or molecules.
- These substances mainly have a constant or uniform composition throughout.
- The substances have fixed boiling and melting points.
- A pure substance usually participates in a chemical reaction to form predictable products.
What is a Mixture?
In chemistry, when two or more substances mix with each other without participating in a chemical change, the resulting substance is called a Mixture.
Types of Mixtures
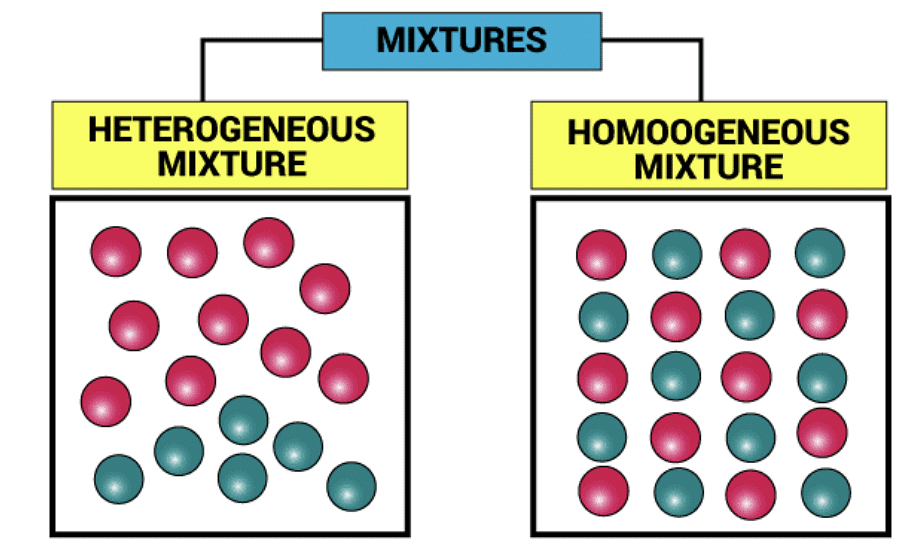 Type of Mixtures
Type of Mixtures
1. Homogeneous mixtures are those whose composition for each part remains constant.
Example: Aqueous and gaseous solution.
2. Heterogeneous mixtures are those whose composition may vary for each and every part.
Example: Soil and concrete mixtures.
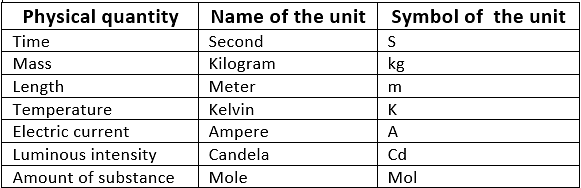
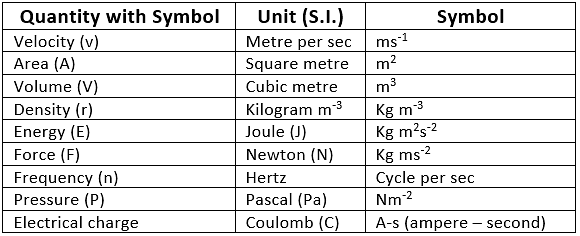
Physical Quantities & their Measurement
1. Fundamental Units
- These units can neither be derived from one another nor can be further resolved into any other units. Seven fundamental units of the S.I. system

2. Derived Units
- These units are the function of more than one fundamental unit

Measurement of Temperature
Three scales of temperature
- Kelvin scale (K)
- Degree Celsius scale (oC)
- Degree Fahrenheit scale (oF)
Relations between the scales:
- oF = 9/5(oC) + 32
- K = oC + 273
0 K temperatures are called absolute zero.
Precision and Accuracy
- Precision: Closeness of outcomes of different measurements taken for the same quantity.
- Accuracy: Agreement of experimental value to the true value
Significant Figures: Rules
- All non-zero digits are significant.
- Zeroes preceding the first non-zero digit are not significant.
- Zeroes between two non-zero digits are significant.
- Zeroes at the end of a number are significant when they are on the right side of the decimal point.
- Counting numbers of objects have infinite significant figures.
Scientific Notation
Numbers are represented in N × 10n form.
Where,
- N = Digit term
- n = exponent having positive or negative value.
Examples:
12540000 = 1.254 × 107
0.00456 = 4.56 ×10-3

Mathematical Operations of Scientific Notation
Multiplication and Division
- Follow the same rules which are for exponential numbers.
Example: (7.0×103)×(8.0×10-7) = (7.0×8.0)×(10[3 + (-7)]) = 56.0×10-4 - Result cannot have more digits to the rite of decimal point than either of the original numbers.
(7.0×103)/(8.0×10-7) = (7.0/8.0)×(10[3 - (-7)]) = 0.875×1010 = 0.9×1010
Addition and Subtraction
- Numbers are written in such a way that they have the same exponent and after that coefficients are added or subtracted.
(5×103) + (8×105) = (5×103) + (800×103) = (5+800)×103 = 805×103 - The result must be reported with no more significant figures as there in the original number with few significant figures.
Rules for limiting the result of mathematical operations:
- If the rightmost digit to be removed is more than 5, the preceding number is increased by one.
- If the rightmost digit to be removed is less than 5, the preceding number is not changed.
- If the rightmost digit to be removed is 5, then the preceding number is not changed if it is an even number but is increased by one if it is an odd number.
Dimensional Analysis
- This is based on the fact that the ratio of each fundamental quantity in one unit with their equivalent quantity in another unit is equal to one.
- Derived unit first expressed in dimension and each fundamental quantities like mass length time are converted in another system of the desired unit to work out the conversion factor
- Original Quantity × Conversion factor = Equivalent Quantity
(In former unit) (In final Unit)
Example: (1 kg/2.205 pound) = 1=(1kg/1000gm)
So 1 kg = 2.205 pound = 1000 gm
Laws of Chemical Combination
1. Law of conservation of mass
“For any chemical change total mass of active reactants are always equal to the mass of the product formed”
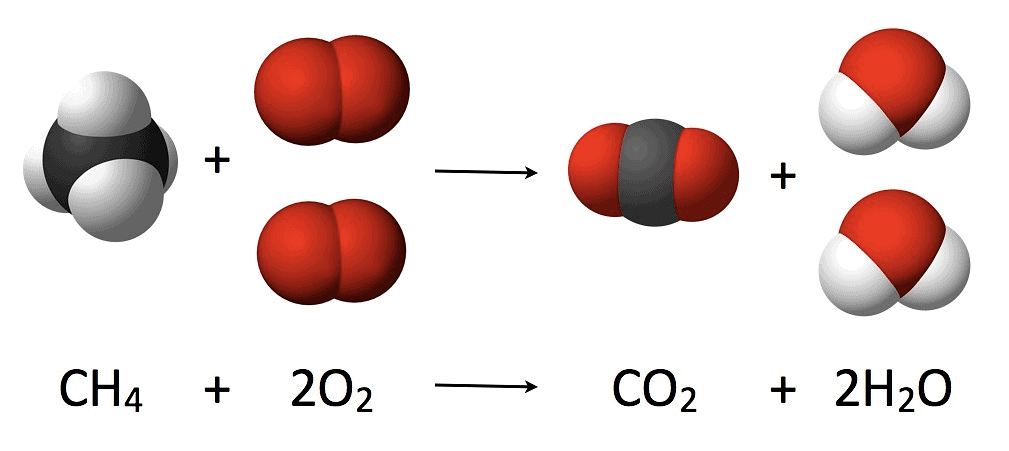 Law of Conservation of Mass
Law of Conservation of Mass
2. Law of constant proportions
A chemical compound always contains same elements in definite proportion by mass and it does not depend on the source of compound.
 Law of Constant Proportions
Law of Constant Proportions
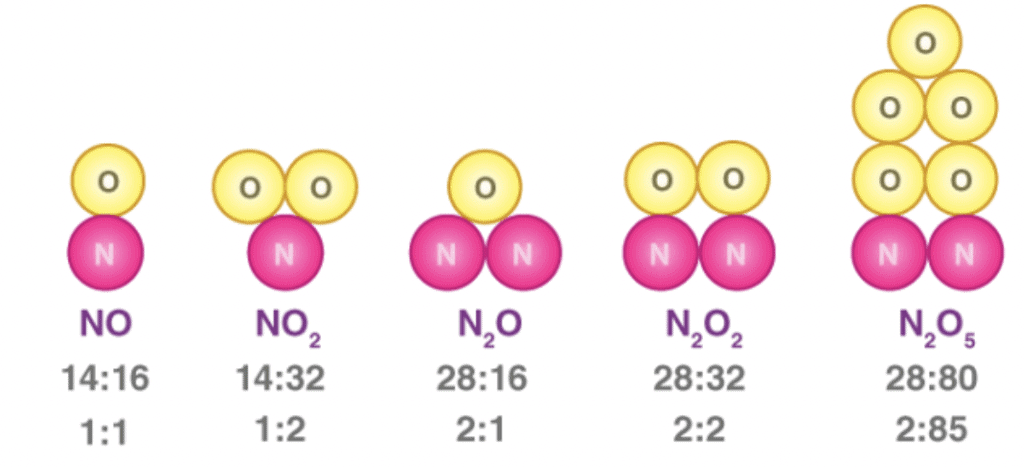
3. Law of multiple proportions
When two elements combine to form two or more than two different compounds then the different masses of one element B which combine with fixed mass of the other element bear a simple ratio to one another.
 Law of Multiple Proportions
Law of Multiple Proportions
4. Law of reciprocal proportion
If two elements B and C react with the same mass of a third element (A), the ratio in which they do so will be the same or simple multiple if B and C reacts with each other.
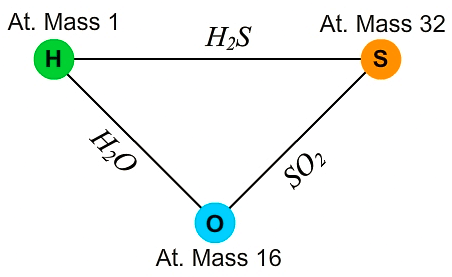 Law of Reciprocal Proportion
Law of Reciprocal Proportion
5. Gay Lussac’s law of combining volumes
At given temperature and pressure the volumes of all gaseous reactants and products bear a simple whole number ratio to each other.
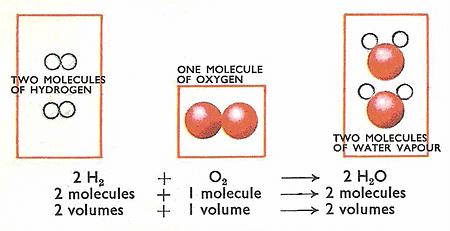 Gay Lussac's Law
Gay Lussac's Law
What is Dalton’s Atomic Theory?
Dalton's atomic theory proposed that all matter was composed of atoms, indivisible and indestructible building blocks. While all atoms of an element were identical, different elements had atoms of differing size and mass.
- Every matter consists of indivisible atoms.
- Atoms can neither be created nor destroyed.
- Atoms of a given element are identical in properties
- Atoms of different elements differ in properties.
- Atoms of different elements combine in a fixed ratio to form a molecule of a compound.

Atomic and Molecular Masses
Atomic Mass
- Mass of an atom.
- Reported in the atomic mass unit “amu” or unified mass “u”
- One atomic mass unit i.e. amu, is the mass exactly equal to one-twelfth the mass of one carbon-12 atom.
Molecular Mass
- Mass of a molecule of the covalent compound.
- It is equal to the sum of the atomic masses of all the elements present in the molecule.
Formula Unit Mass
- Mass of a molecule of an ionic compound
- It is also equal to the sum of the atomic masses of all the elements present in the molecule

Mole Concept
Mole
- Unit of the amount of substance.
- One mole amount of substance that contains as many particles or entities as there are atoms in exactly 12 g of the 12C isotope.
Molar mass
- Mass of one mole of a substance in gram
- Molar mass in gram in numerically equal to atomic/molecular/formula mass in amu or u.
Percentage composition
Mass percentage of an element in a compound = (Mass of that element in the compound/Molecular mass of the compound)×100
Percentage yield
- It is the ratio of the actual yield of the reaction to the theoretical yield multiplied by 100.
- % yield = (Actual yield /Theoretical yield)×100
Empirical Formula and Molecular Formula
Molecular Formula
Represents the actual number of each individual atom in any molecule is known as the molecular formula.
Empirical Formula
Expresses the smallest whole number ratio of the constituent atom within the molecule.
Molecular formula = (Empirical formula)n
Molecular weight = n × Empirical weight
also,
Molecular weight = 2 × Vapour density
Limiting Reagent
- The reactant which is totally consumed during the course of reaction and when it is consumed reaction stops.
- For a balanced reaction reaction:
A +B → C + D
B would be a limiting reagent if nA / nB>nB/nA
Similarly, A is a limiting reagent if nA / nB<nB/nA
Concentration of the Solutions

Mass by Mass Percentage
- Amount of solute in gram present per 100 gm of the solution.
- Mass percentage of solute = [(Mass of solute)/(Mass of solution)] x100
- Mass by Volume Percentage
- Amount solute in gram present per 100 mL of the solution.
Volume by Volume Percentage
- The volume of solute per 100 mL of the solution
- Volume by volume percentage of solute = [(Volume of solute)/(volume of solution)] x100
Parts per million (ppm)
- The amount of solute in grams per million (106) grams of the solution.
- ppm = [(mass of solute/mass of solution)]x 106
Mole fraction
- Ratio of the moles of one component of the solution to the total number of moles of solution.
- Total mole fraction of all the components of a solution is equal to 1.
- For binary solutions having two components A and B
Mole fraction of A
XA = (nA)/(nA+nB)]
Mole fraction of B
XB = (nB)/(nA+nB)]
or XB = 1- XA
Molarity (M)
- Number of moles of solute per 1000 mL of the solution.
- M = (Number of moles of solute)/(Volume of solution in L)
Molality (m)
- The number of moles of solute per 1000 grams of the solvent.
- m = (Number of moles of solute)/(Weight of solvent in kg)
|
357 docs|148 tests
|
FAQs on Some Basic Concepts in Chemistry Class 11 Notes Chemistry
| 1. What is the difference between a pure substance and a mixture? |  |
| 2. How do you measure physical quantities accurately? |  |
| 3. What are significant figures and why are they important in scientific measurements? |  |
| 4. What are the laws of chemical combination? |  |
| 5. What is Dalton’s Atomic Theory and its significance in chemistry? |  |

|
Explore Courses for JEE exam
|

|