Matrices Class 12 Notes Maths Chapter 3
- Two matrices are said to be equal if they have the same order and each element of one is equal to the corresponding element of the other.
- An m x n matrix A is said to be a square matrix if m = n i.e. number of rows = number of columns.
- In a square matrix the diagonal from left hand side upper corner to right hand side lower corner is known as leading diagonal or principal diagonal.
- The sum of the elements of a square matrix A lying along the principal diagonal is called the trace of A i.e. tr(A). Thus if A = [aij]n×n, then tr(A) = ∑ni=1 aii = a11 + a22 +......+ ann.
- For a square matrix A = [aij]n×n, if all the elements other than in the leading diagonal are zero i.e. aij = 0, whenever i ≠ j then A is said to be a diagonal matrix.
- A matrix A = [aij]n×n is said to be a scalar matrix if aij = 0, i ≠ j = m, i =j, where m≠ 0
Properties of various types of matrices:
Given a square matrix A = [aij]n×n,
1) For upper triangular matrix, aij = 0, ∀ i > j
2) For lower triangular matrix, aij = 0, ∀ i < j
3) Diagonal matrix is both upper and lower triangular
4) A triangular matrix A = [aij]n×n is called strictly triangular if aii = 0 for ∀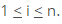
If A = [aij]m×n and transpose of A i.e. A' = [bij]n×m then bij =aji, ∀i, j.
Properties of Transpose:
1) (A')' = A
2) (A + B)' = A' + B', A and B being conformable matrices
3) (αA)' = αA', α being scalar
4) (AB)' = B'A', A and B being conformable for multiplication
Properties of Transpose conjugate:
1) (Aθ)θ = A
2) (A + B)θ = Aθ + Bθ
3) (kA)θ = Aθ, k being any number
4) (AB)θ = BθAθ
Some chief properties of matrices:
1) Only matrices of the same order can be added or subtracted.
2) Addition of matrices is commutative as well as associative.
3) Cancellation laws hold well in case of addition.
4) The equation A + X = 0 has a unique solution in the set of all m × n matrices.
5) All the laws of ordinary algebra hold for the addition or subtraction of matrices and their multiplication by scalar.
Matrix Multiplication:
1) Matrix multiplication may or may not be commutative. i.e., AB may or may not be equal to BA
2) If AB = BA, then matrices A and B are called Commutative Matrices.
3) If AB = BA, then matrices A and B are called Anti-Commutative Matrices.
4) Matrix multiplication is Associative
5) Matrix multiplication is Distributive over Matrix Addition.
6) Cancellation Laws need not hold goodin case of matrix multiplication i.e., if AB = AC then B may or may not be equal to Ceven if A ≠ 0.
7) AB = 0 i.e., Null Matrix, does not necessarily imply that either A or B is a null matrix.
A square matrix A = [aij] is said to be symmetric when aij = aji for all i and j.
If aij = -aji for all i and j and all the leading diagonal elements are zero, then the matrix is called a skew symmetric matrix.
A square matrix A = [aij] is said to be Hermitian matrix if Aθ = A.
1) Every diagonal element of a Hermitian Matrix is real.
2) A Hermitian matrix over the set of real numbers is actually a real symmetric matrix.A square matrix, A = [aij] is said to be a skew-Hermitian matrix if Aθ = -A.
1) If A is a skew-Hermitian matrix then the diagonal elements must be either purely imaginary or zero.
2) A skew-Hermitian Matrix over the set of real numbers is actually a real skew- symmetric matrix.Any square matrix A of order n is said to be orthogonal if AA' = A'A = In.
A matrix such that A2 = I is called involuntary matrix.
Let A be a square matrix of order n. Then A(adj A) = |A| In = (adj A)A.
The adjoint of a square matrix of order 2 can be easily obtained by interchanging the diagonal elements and changing the signs of off-diagonal (left hand side lower corner to right hand side upper corner) elements.
A non-singular square matrix of order n is invertible if there exists a square matrix B of the same order such that AB = In = BA.
The inverse of A is given by A-1 = 1/|A|.adj A.
Properties of Inverse of a matrix:
1) Every invertible matrix possesses a unique inverse.
2) If A and B are invertible matrices of the same order, then AB is invertible and (AB)-1 = B-1A-1. This is also termed as the reversal law.
3) In general,if A,B,C,...are invertible matrices then (ABC....)-1 =..... C-1 B-1 A-1.
4) If A is an invertible square matrix, then AT is also invertible and (AT)-1 = (A-1)T.- If A is a non-singular square matrix of order n, then |adj A| = |A|n-1.
- If A and B are non-singular square matrices of the same order, then adj (AB) = (adj B) (adj A).
- If A is an invertible square matrix, then adj(AT) = (adj A)T.
- If A is a non-singular square matrix, then adj(adjA) = |A|n-1A.
The following three operations can be applied on rows or columns of a matrix:
1) Interchange of any two rows (columns)
2) Multiplying all elements of a row (column) of a matrix by a non-zero scalar. If the elements of ith row (column) are multiplied by non-zero scalar k, it will be denoted by Rl→Ri (k) [Ci→Ci (k)] or Rl→kRi [Ci→kCi].
3) Adding to the elements of a row (column), the corresponding elements of any other row (column) multiplied by any scalar k.A number ‘r’ is called the rank of a matrix if:
1) Every square sub matrix of order (r +1) or more is singular.
2) There exists at least one square sub matrix of order r which is non-singular.It also equals the number of non-zero rows in the row echelon form of the matrix.
|
517 docs|120 tests
|
FAQs on Matrices Class 12 Notes Maths Chapter 3
| 1. What is a matrix in the context of JEE? |  |
| 2. How is matrix multiplication performed in JEE? |  |
| 3. What is the determinant of a matrix in JEE? |  |
| 4. How can I find the inverse of a matrix in JEE? |  |
| 5. What are the applications of matrices in JEE? |  |
















