Q. 91. A car moves uniformly along a horizontal sine curve y = a sin (x/α), where a and α are certain constants. The coefficient of friction between the wheels and the road is equal to k. At what velocity will the car ride without sliding?
Ans. Since the car follows a curve, so the maximum velocity at which it can ride without sliding at the point of minimum radius of curvature is the sought velocity and obviously in this case the static friction between the car and the road is limiting.
Hence from the equation Fn = mw

so  (1)
(1)
We know that, radius of curvature for a curve at any point (x, y) is given as,
 (2)
(2)
For the given curve,

Substituting this value in (2) we get,

For the minimum 
and therefore, corresponding radius of curvature
 (3)
(3)
Hence from (1) and (2)

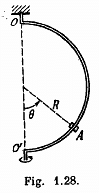
Q. 92. A chain of mass m forming a circle of radius R is slipped on a smooth round cone with half-angle θ. Find the tension of the chain if it rotates with a constant angular velocity co about a vertical axis coinciding with the symmetry axis of the cone.
Ans. The sought tensile stress acts on each element of the chain. Hence divide the chain into small, similar elements so that each element may be assumed as a particle. We consider one such element of mass dm, which subtends angle d α at the centre. The chain moves along a circle of known radius R with a known angular speed ω and certain forces act on it We have to find one of these forces.
From Newton’s second law in projection form, Fx = mwx we get


Then putting 



Q. 93. A fixed pulley carries a weightless thread with masses m1 and m2 at its ends. There is friction between the thread and the pulley. It is such that the thread starts slipping when the ratio m2/m1 = η0. Find:
(a) the friction coefficient;
(b) the acceleration of the masses when m2/m1 = η > η0.
Ans. Let, us consider a small element of the thread and draw free body diagram for this element, (a) Applying Newton’s second law of motion in projection form, Fn = mwn for this element,

or,  (1)
(1)
Also,  (2)
(2)


(b) When  Svhich is greater than η0 the blocks will move with same value of acceleration, (say w) and clearly m2 moves downward. From Newton’s second law in projection form (downward for m2 and upward for m1) we get :
Svhich is greater than η0 the blocks will move with same value of acceleration, (say w) and clearly m2 moves downward. From Newton’s second law in projection form (downward for m2 and upward for m1) we get :
 (4)
(4)
and  (5)
(5)
Also  (6)
(6)
Simultaneous solution of Eqs. (4), (5) and (6) yields :

Q. 94. A particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0 and forms an angle α with the horizontal.
Ans. The force with which the cylinder wall acts on the particle will provide centripetal force necessary for the motion of the particle> and since there is no acceleration acting in the horizontal direction, horizontal component of the velocity will remain constant througout the motion.

So vx = v0 cos α
Using, Fn = m wn, for the particle of mass m,

which is the required normal force.
Q. 95. Find the magnitude and direction of the force acting on the particle of mass m during its motion in the plane xy according to the law x = a sin ωt, y = b cos ωt, where a, b, and ω are constants.
Ans. Obviously the radius vector describing the position of the particle relative to the origin of coordinate is

Differentiating twice with respect the time :
 (1)
(1)
Thus 
Q. 96. A body of mass m is thrown at an angle to the horizontal with the initial velocity v0. Assuming the air drag to be negligible, find:
(a) the momentum increment Δp that the body acquires over the first t seconds of motion;
(b) the modulus of the momentum increment Δp during the total time of motion.
Ans. 
 (1)
(1)
(b) Using the solution of problem 1.28 (b), the total time of motion 
Hence using 


Q. 97. At the moment t = 0 a stationary particle of mass in experiences a time-dependent force F = at (τ — t), where a is a constant vector, τ is the time during which the given force acts. Find:
(a) the momentum of the particle when the action of the force discontinued;
(b) the distance covered by the particle while the force acted.
Ans. From the equation o f the g iven time dependence force  the force vanishes,
the force vanishes,
(a) Thus 
or, 
but 
(b) Again from the equation 
or, 
Integrating w ithin the limits for 

or, 
Thus 
Hence distance covered during the tim e interval t = τ,


Q. 98. At the moment t = 0 a particle of mass m starts moving due to a force F = F0 sin ωt, where F0 and ω are constants. Find the distance covered by the particle as a function of t. Draw the approximate plot of this function.
Ans. We have 
or 
On integrating,

When


Thus 

Q. 99. At the moment t = 0 a particle of mass m starts moving due to a force F = F0 cos ωt, where F0 and ω are constants. How long will it be moving until it stops for the first time? What distance will it traverse during that time? What is the maximum velocity of the particle over this distance?
Ans. According to the problem, the force acting on the particle of mass m  cos ωt
cos ωt
So, 
Integrating, within the limits.

It is clear from equation (1), that after starting at t = 0, die particle comes to rest fro the first time at 
From Eqn. (1),  (2)
(2)
Thus during the time interval t = π/ω, the sought distance

From Eq. (1)

Q. 100. A motorboat of mass m moves along a lake with velocity v0. At the moment t = 0 the engine of the boat is shut down. Assuming the resistance of water to be proportional to the velocity of the boat F = —rv, find:
(a) how long the motorboat moved with the shutdown engine;
(b) the velocity of the motorboat as a function of the distance covered with the shutdown engine, as well as the total distance covered till the complete stop;
(c) the mean velocity of the motorboat over the time interval (beginning with the moment t = 0), during which its velocity decreases η times.
Ans. (a) From the problem 
Thus 
or, 
On integrating 
But at 
or, 
Thus for 
(b) We have 
Integrating within the given limits to obtain v (s):
or, 
Thus for 

Now, average velocity over this time interval,

Q. 101. Having gone through a plank of thickness h, a bullet changed its velocity from v0 to v. Find the time of motion of the bullet in the plank, assuming the resistance force to be proportional to the square of the velocity.
Ans. According to the problem

Integrating, withing the limits,

To find the valufc of k, rewrite

On integrating

So,  (2)
(2)
Putting the value of k from (2) in (1), we get

Q. 102. A small bar starts sliding down an inclined plane forming an angle α with the horizontal. The friction coefficient depends on the distance x covered as k = ax, where a is a constant. Find the distance covered by the bar till it stops, and its maximum velocity over this distance.
Ans. From Newton’s second law for the bar in projection from, Fx = m wx along x direction
we get 
or, 
or, 
or, 



As the motion of the bar is unidirectional it stops after going through a distance of 


Hence, the maximum velocity will be at the distance, x = tan α/a Putting this value of x in (1) the maximum velocity,

Q. 103. A body of mass m rests on a horizontal plane with the friction coefficient lc. At the moment t = 0 a horizontal force is applied to it, which varies with time as F = at, where a is a constant vector. Find the distance traversed by the body during the first t seconds after the force action began.
Ans. Since, the applied force is proportional to the time and the frictional force also exists, the motion does not start just after applying the force. The body starts its motion when F equals the limiting friction.
Let the motion start after time t0 , then

 the body remains at rest and for t > t0 obviously
the body remains at rest and for t > t0 obviously


Q. 104. A body of mass m is thrown straight up with velocity vo. Find the velocity v' with which the body comes down if the air drag equals kv2, where k is a constant and v is the velocity of the body.
Ans. While going upward, from Newton’s second law in vertical direction :

At the maximum height h, the speed v = 0, so

Integrating and solving, we get,
 (1)
(1)
When the body falls downward, the net force acting on the body in downward direction equals 
Hence net acceleration, in downward direction, according to second law of motion

Thus, 
Integrating and putting the value of h from (1), we get,

Q. 105. A particle of mass m moves in a certain plane P due to a force F whose magnitude is constant and whose vector rotates in that plane with a constant angular velocity ω. Assuming the particle to be stationary at the moment t = 0, find:
(a) its velocity as a function of time;
(b) the distance covered by the particle between two successive stops, and the mean velocity over this time.

Ans. Let us fix x - y co-ordinate system to the given plane, taking x-axis in the direction along which the force vector was oriented at the moment t = 0 , then the fundamental equation of dynamics expressed via the projection on x and y-axes gives,
 (1)
(1)
and  (2)
(2)
(a) Using the condition  (3)
(3)
and
 (4)
(4)
Hence, 
(b) It is seen from this that the velocity v turns into zero after the time interval Δt, which can be found from the relation ,
 Consequently, the sought distance, is
Consequently, the sought distance, is




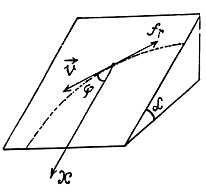
Q. 106. A small disc A is placed on an inclined plane forming an angle a with the horizontal (Fig. 1.27) and is imparted an initial velocity v0. Find how the velocity of the disc depends on the angle y if the friction coefficient k = tan α and at the initial moment yo = = π/2.
Ans. The acceleration of the disc along the plane is determined by the projection of the force of gravity on this plane Fx = mg sin α and the friction force fr = kmg cos α . In our case k = tan α and therefore
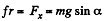
Let us find the projection of the acceleration on the derection of the tangent to the trajectory and on the x-axis :
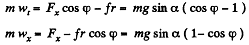
It is seen fromthis that wt = - wx, which means that the velocity v and its projection vx differ only by a constant value C which does not change with time, i.e.
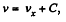
where 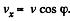 . The constant C is found from the initial condition v = v0, whence
. The constant C is found from the initial condition v = v0, whence 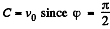 initially. Finally we obtain
initially. Finally we obtain
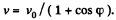
In the cource of time 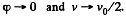 (Motion then is unaccelerated.)
(Motion then is unaccelerated.)
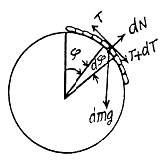
Q. 107. A chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain 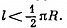
Ans. Let us consider an element of length ds at an angle qp from the vertical diameter. As the speed of this element is zero at initial instant of time, it's centripetal acceleration is zero, and hence, 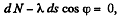 where λ is the linear mass density o f the chain Let
where λ is the linear mass density o f the chain Let 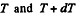 be the tension at the upper and the lower ends of ds. we have from,
be the tension at the upper and the lower ends of ds. we have from, 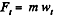
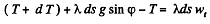
or, 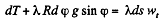
If we sum the above equation for all elements, the term 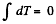 because there is no tension at the free ends, so
because there is no tension at the free ends, so
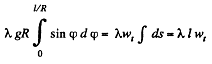
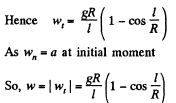
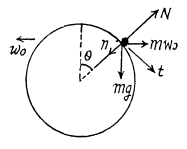
Q. 108. A small body is placed on the top of a smooth sphere of radius R. Then the sphere is imparted a constant acceleration w0 in the horizontal direction and the body begins sliding down. Find:
(a) the velocity of the body relative to the sphere at the moment of break-off;
(b) the angle θ0 between the vertical and the radius vector drawn from the centre of the sphere to the break-off point; calculate θ0 for w0 = g.
Ans. In the problem, we require the velocity of the body, realtive to the sphere, which itself moves with an acceleration w0 in horizontal direction (say towards left). Hence it is advisible to solve the problem in the frame of sphere (non-inertial frame).
At an arbitary moment, when the body is at an angle θ with the vertical, we sketch the force diagram for the body and write the second law of motion in projection form
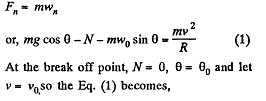
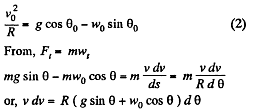
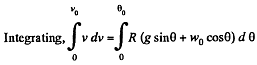
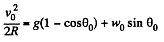 (3)
(3)
Note that the Eq. (3) can also be obtained by the work-energy theorem A = ΔT (in the frame of sphere)
therefore, 
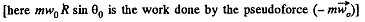
or, 
Solving Eqs. (2) and (3) we get,
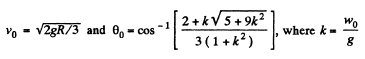
Hence 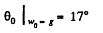
Q. 109. A particle moves in a plane under the action of a force which is always perpendicular to the particle's velocity and depends on a distance to a certain point on the plane as 1/rn, where n is a constant. At what value of n will the motion of the particle along the circle be steady?
Ans. This is not central force problem unless the path is a circle about the said point. Rather here Ft (tangential force) vanishes. Thus equation of motion becomes,
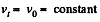
and, 
We can consider the latter equation as the equilibrium under two forces. When the motion is perturbed, we write r = r0 + x and the net force acting on the particle is,

This is opposite to the displacement 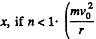 is an outward directed centrifiigul force while
is an outward directed centrifiigul force while 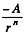 is thd inward directed external force).
is thd inward directed external force).
Q. 110. A sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R (Fig. 1.28). The system is set in rotation with a constant angular velocity ω about a vertical axis OO'. Find the angle θ corresponding to the steady position of the sleeve.
Ans. There are two forces on the sleeve, the weight F1 and the centrifugal force F2. We resolve both forces into tangential and normal component then the net downward tangential force on the sleeve is,
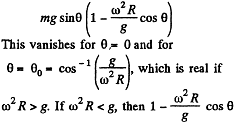
is always positive for small values of 0 and hence the net tangential force near θ = 0 opposes any displacement away from it. θ = 0 is then stable.
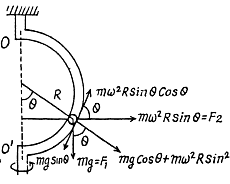
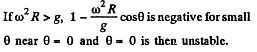
However 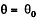 is stable because the force tends to bring the sleeve near the equilibrium position
is stable because the force tends to bring the sleeve near the equilibrium position 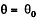
If ω2R = g, the two positions coincide and becomes a stable equilibrium point.
Q. 111. A rifle was aimed at the vertical line on the target located precisely in the northern direction, and then fired. Assuming the air drag to be negligible, find how much off the line, and in what direction, will the bullet hit the target. The shot was fired in the horizontal direction at the latitude φ = 60°, the bullet velocity v = 900 m/s, and the distance from the target equals s = 1.0 km.
Ans. Define the axes as shown with z along the local vertical, x due east and y due north. (We assume we are in the northern hemisphere). Then the Coriolis force has the components.
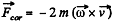
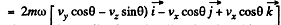
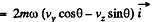
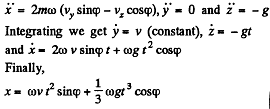
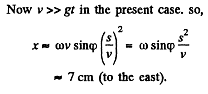
Q. 112. A horizontal disc rotates with a constant angular velocity ω = 6.0 rad/s about a vertical axis passing through its centre. A small body of mass m = 0.50 kg moves along a diameter of the disc with a velocity v' = 50 cm/s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r = 30 cm from the rotation axis.
Ans. The disc exerts three forces which are mutually perpendicular. They are the reaction of the weight, mgy vertically upward, the Coriolis force 2mv' ω perpendicular to the plane of the vertical and along the diameter, and mω2r outward along the diameter. The resultant force is,
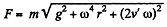
Q. 113. A horizontal smooth rod AB rotates with a constant angular velocity ω = 2.00 rad/s about a vertical axis passing through its end A. A freely sliding sleeve of mass m = 0.50 kg moves along the rod from the point A with the initial velocity v0 = 1.00 m/s. Find the Coriolis force acting on the sleeve (in the reference frame fixed to the rotating rod) at the moment when the sleeve is located at the distance r = 50 cm from the rotation axis.
Ans. The sleeve is free to slide along the rod AB. Thus only the centrifugal force acts on it.
The equation is,
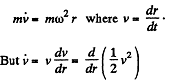
so, 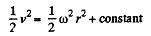
or, 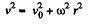
v0 being the initial velocity when r = 0. The Coriolis force is then,
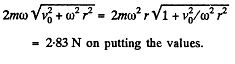
Q. 114. A horizontal disc of radius R rotates with a constant angular velocity ω about a stationary vertical axis passing through its edge. Along the circumference of the disc a particle of mass m moves with a velocity that is constant relative to the disc. At the moment when the particle is at the maximum distance from the rotation axis, the resultant of the inertial forces Fin acting on the particle in the reference frame fixed to the disc turns into zero. Find:
(a) the acceleration ω' of the particle relative to the disc;
(b) the dependence of Fin on the distance from the rotation axis.
Ans. The disc OBAC is rotating with angular velocity ω about the axis OO' passing through the edge point O. The equation of motion in rotating frame is,
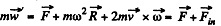
where 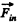 is the resultant inertial force. (pseudo force) which is the vector sum of centrifugal and Coriolis forces.
is the resultant inertial force. (pseudo force) which is the vector sum of centrifugal and Coriolis forces.
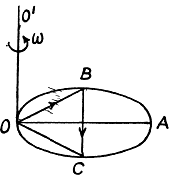
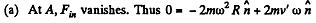
where  the inward drawn unit vector to the centre from the point in question, here A.
the inward drawn unit vector to the centre from the point in question, here A.
Thus, 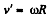
so, 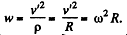
(b) At B 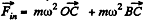
its magnitude is 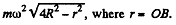
Q. 115. A small body of mass m = 0.30 kg starts sliding down from the top of a smooth sphere of radius R = 1.00 m. The sphere rotates with a constant angular velocity ω = 6.0 rad/s about a vertical axis passing through its centre. Find the centrifugal force of inertia and the Coriolis force at the moment when the body breaks off the surface of the sphere in the reference frame fixed to the sphere.
Ans. The equation of motion in the rotating coordinate system is,
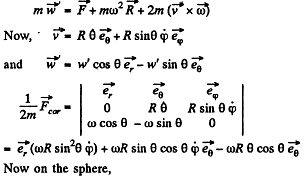
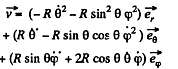
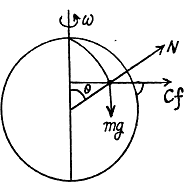
Thus the equation of motion are,

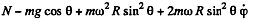
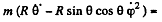
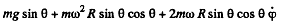
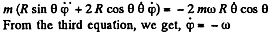
A result that is easy to understant by considering the motion in non-rotating frame. The eliminating φ we get,
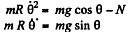
Integrating the last equation
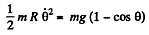
Hence
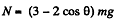
So the body must fly off for 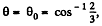 exactly as if the sphere were nonrotating.
exactly as if the sphere were nonrotating.
Now, at this point 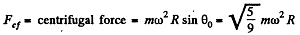
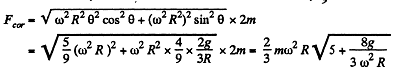
Q.116. A train of mass m = 2000 tons moves in the latitude φ = 60° North. Find:
(a) the magnitude and direction of the lateral force that the train exerts on the rails if it moves along a meridian with a velocity v = 54 km per hour;
(b) in what direction and with what velocity the train should move for the resultant of the inertial forces acting on the train in the reference frame fixed to the Earth to be equal to zero.
Ans. (a) When the train is moving along a meridian only the Coriolis force has a lateral component and its magnitude (see the previous problem) is,
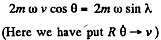
So, 
= 3.77 kN, (we write λ for the latitude)
(b) The resultant of the inertial forces acting on the train is,
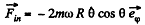
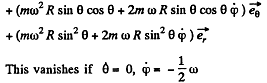
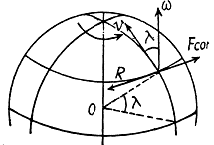
Thus 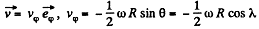
(We write λ for the latitude here)
Thus the train must move from the east to west along the 60th parallel with a speed,

Q. 117. At the equator a stationary (relative to the Earth) body falls down from the height h = 500 m. Assuming the air drag to be negligible, find how much off the vertical, and in what direction, the body will deviate when it hits the ground.
Ans. We go to the equation given in 1.111. Here vy = 0 so we can take y = 0, thus we get for the motion in the  .
.
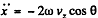
and 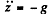
Integrating, 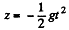

So 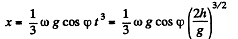
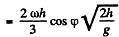
There is thus a displacement to the east of
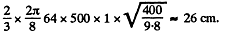
Q. 106. A small disc A is placed on an inclined plane forming an angle a with the horizontal (Fig. 1.27) and is imparted an initial velocity v0. Find how the velocity of the disc depends on the angle y if the friction coefficient k = tan α and at the initial moment yo = = π/2.
Ans. The acceleration of the disc along the plane is determined by the projection of the force of gravity on this plane Fx = mg sin α and the friction force fr = kmg cos α . In our case k = tan α and therefore
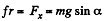
Let us find the projection of the acceleration on the derection of the tangent to the trajectory and on the x-axis :
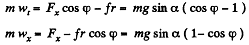
It is seen fromthis that wt = - wx, which means that the velocity v and its projection vx differ only by a constant value C which does not change with time, i.e.

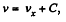
where 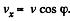 . The constant C is found from the initial condition v = v0, whence
. The constant C is found from the initial condition v = v0, whence 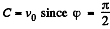 initially. Finally we obtain
initially. Finally we obtain
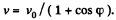
In the cource of time 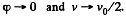 (Motion then is unaccelerated.)
(Motion then is unaccelerated.)
Q. 107. A chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain 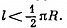
Ans. Let us consider an element of length ds at an angle qp from the vertical diameter. As the speed of this element is zero at initial instant of time, it's centripetal acceleration is zero, and hence, 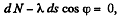 where λ is the linear mass density o f the chain Let
where λ is the linear mass density o f the chain Let 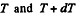 be the tension at the upper and the lower ends of ds. we have from,
be the tension at the upper and the lower ends of ds. we have from, 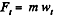
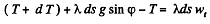
or, 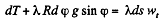
If we sum the above equation for all elements, the term 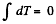 because there is no tension at the free ends, so
because there is no tension at the free ends, so
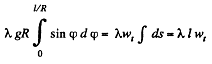

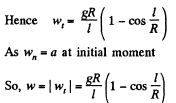
Q. 108. A small body is placed on the top of a smooth sphere of radius R. Then the sphere is imparted a constant acceleration w0 in the horizontal direction and the body begins sliding down. Find:
(a) the velocity of the body relative to the sphere at the moment of break-off;
(b) the angle θ0 between the vertical and the radius vector drawn from the centre of the sphere to the break-off point; calculate θ0 for w0 = g.
Ans. In the problem, we require the velocity of the body, realtive to the sphere, which itself moves with an acceleration w0 in horizontal direction (say towards left). Hence it is advisible to solve the problem in the frame of sphere (non-inertial frame).
At an arbitary moment, when the body is at an angle θ with the vertical, we sketch the force diagram for the body and write the second law of motion in projection form
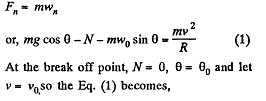
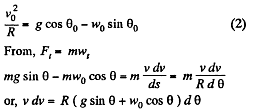

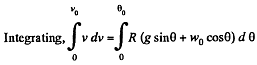
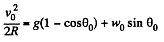 (3)
(3)
Note that the Eq. (3) can also be obtained by the work-energy theorem A = ΔT (in the frame of sphere)
therefore, 
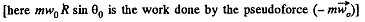
or, 
Solving Eqs. (2) and (3) we get,
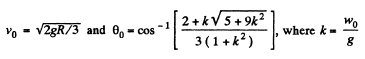
Hence 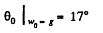
Q. 109. A particle moves in a plane under the action of a force which is always perpendicular to the particle's velocity and depends on a distance to a certain point on the plane as 1/rn, where n is a constant. At what value of n will the motion of the particle along the circle be steady?
Ans. This is not central force problem unless the path is a circle about the said point. Rather here Ft (tangential force) vanishes. Thus equation of motion becomes,
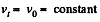
and, 
We can consider the latter equation as the equilibrium under two forces. When the motion is perturbed, we write r = r0 + x and the net force acting on the particle is,

This is opposite to the displacement 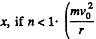 is an outward directed centrifiigul force while
is an outward directed centrifiigul force while 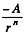 is thd inward directed external force).
is thd inward directed external force).
Q. 110. A sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R (Fig. 1.28). The system is set in rotation with a constant angular velocity ω about a vertical axis OO'. Find the angle θ corresponding to the steady position of the sleeve.
Ans. There are two forces on the sleeve, the weight F1 and the centrifugal force F2. We resolve both forces into tangential and normal component then the net downward tangential force on the sleeve is,
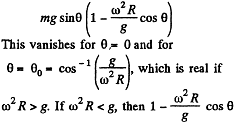
is always positive for small values of 0 and hence the net tangential force near θ = 0 opposes any displacement away from it. θ = 0 is then stable.

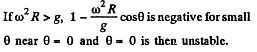
However 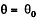 is stable because the force tends to bring the sleeve near the equilibrium position
is stable because the force tends to bring the sleeve near the equilibrium position 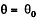
If ω2R = g, the two positions coincide and becomes a stable equilibrium point.
Q. 111. A rifle was aimed at the vertical line on the target located precisely in the northern direction, and then fired. Assuming the air drag to be negligible, find how much off the line, and in what direction, will the bullet hit the target. The shot was fired in the horizontal direction at the latitude φ = 60°, the bullet velocity v = 900 m/s, and the distance from the target equals s = 1.0 km.
Ans. Define the axes as shown with z along the local vertical, x due east and y due north. (We assume we are in the northern hemisphere). Then the Coriolis force has the components.
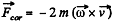
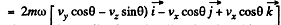
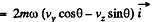
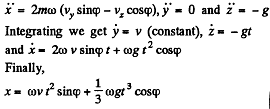

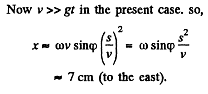
Q. 112. A horizontal disc rotates with a constant angular velocity ω = 6.0 rad/s about a vertical axis passing through its centre. A small body of mass m = 0.50 kg moves along a diameter of the disc with a velocity v' = 50 cm/s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r = 30 cm from the rotation axis.
Ans. The disc exerts three forces which are mutually perpendicular. They are the reaction of the weight, mgy vertically upward, the Coriolis force 2mv' ω perpendicular to the plane of the vertical and along the diameter, and mω2r outward along the diameter. The resultant force is,
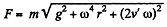
Q. 113. A horizontal smooth rod AB rotates with a constant angular velocity ω = 2.00 rad/s about a vertical axis passing through its end A. A freely sliding sleeve of mass m = 0.50 kg moves along the rod from the point A with the initial velocity v0 = 1.00 m/s. Find the Coriolis force acting on the sleeve (in the reference frame fixed to the rotating rod) at the moment when the sleeve is located at the distance r = 50 cm from the rotation axis.

Ans. The sleeve is free to slide along the rod AB. Thus only the centrifugal force acts on it.
The equation is,
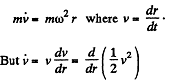
so, 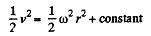
or, 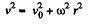
v0 being the initial velocity when r = 0. The Coriolis force is then,
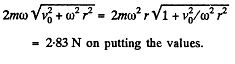
Q. 114. A horizontal disc of radius R rotates with a constant angular velocity ω about a stationary vertical axis passing through its edge. Along the circumference of the disc a particle of mass m moves with a velocity that is constant relative to the disc. At the moment when the particle is at the maximum distance from the rotation axis, the resultant of the inertial forces Fin acting on the particle in the reference frame fixed to the disc turns into zero. Find:
(a) the acceleration ω' of the particle relative to the disc;
(b) the dependence of Fin on the distance from the rotation axis.
Ans. The disc OBAC is rotating with angular velocity ω about the axis OO' passing through the edge point O. The equation of motion in rotating frame is,
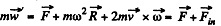
where 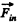 is the resultant inertial force. (pseudo force) which is the vector sum of centrifugal and Coriolis forces.
is the resultant inertial force. (pseudo force) which is the vector sum of centrifugal and Coriolis forces.

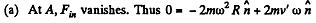
where  the inward drawn unit vector to the centre from the point in question, here A.
the inward drawn unit vector to the centre from the point in question, here A.
Thus, 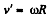
so, 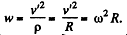
(b) At B 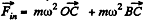
its magnitude is 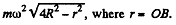
Q. 115. A small body of mass m = 0.30 kg starts sliding down from the top of a smooth sphere of radius R = 1.00 m. The sphere rotates with a constant angular velocity ω = 6.0 rad/s about a vertical axis passing through its centre. Find the centrifugal force of inertia and the Coriolis force at the moment when the body breaks off the surface of the sphere in the reference frame fixed to the sphere.
Ans. The equation of motion in the rotating coordinate system is,
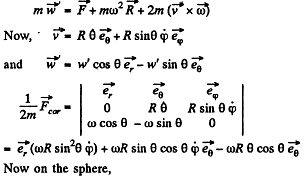
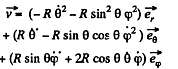

Thus the equation of motion are,

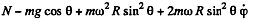
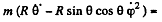
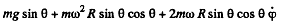
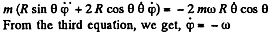
A result that is easy to understant by considering the motion in non-rotating frame. The eliminating φ we get,
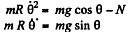
Integrating the last equation
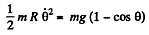
Hence
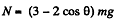
So the body must fly off for 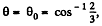 exactly as if the sphere were nonrotating.
exactly as if the sphere were nonrotating.
Now, at this point 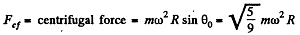
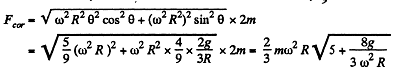
Q. 116. A train of mass m = 2000 tons moves in the latitude φ = 60° North. Find:
(a) the magnitude and direction of the lateral force that the train exerts on the rails if it moves along a meridian with a velocity v = 54 km per hour;
(b) in what direction and with what velocity the train should move for the resultant of the inertial forces acting on the train in the reference frame fixed to the Earth to be equal to zero.
Ans. (a) When the train is moving along a meridian only the Coriolis force has a lateral component and its magnitude (see the previous problem) is,
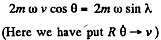
So, 
= 3.77 kN, (we write λ for the latitude)
(b) The resultant of the inertial forces acting on the train is,
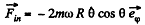
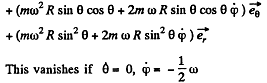

Thus 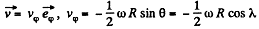
(We write λ for the latitude here)
Thus the train must move from the east to west along the 60th parallel with a speed,

Q. 117. At the equator a stationary (relative to the Earth) body falls down from the height h = 500 m. Assuming the air drag to be negligible, find how much off the vertical, and in what direction, the body will deviate when it hits the ground.
Ans. We go to the equation given in 1.111. Here vy = 0 so we can take y = 0, thus we get for the motion in the  .
.
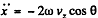
and 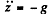
Integrating, 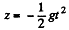

So 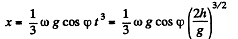
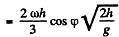
There is thus a displacement to the east of
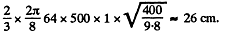
FAQs on Irodov Solutions: The Fundamental Equation of Dynamics - 2 - JEE
| 1. What is the fundamental equation of dynamics? |  |
| 2. How is the fundamental equation of dynamics applied in real-life situations? |  |
| 3. Can the fundamental equation of dynamics be applied to objects with variable mass? |  |
| 4. What are some other important equations related to dynamics? |  |
| 5. How does the fundamental equation of dynamics relate to inertia? |  |

|
Explore Courses for JEE exam
|

|


















