Irodov Solutions: Laws of Conservation of Energy, Momentum & Angular Momentum - 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 141. A horizontal plane supports a plank with a bar of mass m = 1.0 kg placed on it and attached by a light elastic non-deformed cord of length l0 = 40 cm to a point O (Fig. 1.35). The coefficient of friction between the bar and the plank equals k = 0.20. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord deviates from the vertical by an angle θ = 30°. Find the work that has been performed by that moment by the friction force acting on the bar in the reference frame fixed to the plane.
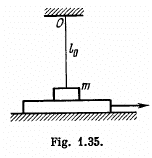
Ans. Obviously the elongation in the cord, Δl = l0 (sec θ - 1), at the moment the sliding first starts and at the moment horizontal projection of spring force equals the limiting friction.
So, 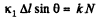 (1)
(1)
(where kx is the elastic constant)
From Newton's law in projection form along vertical direction :
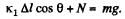
or, 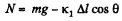 (2)
(2)
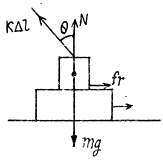
From (1) and (2),
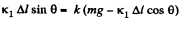

From the equation of the increment of mechanical energy : ΔU + ΔT = Afr
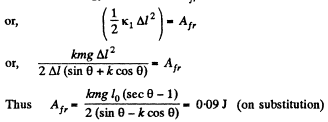
Q. 142. A smooth light horizontal rod AB can rotate about a vertical axis passing through its end A. The rod is fitted with a small sleeve of mass m attached to the end A by a weightless spring of length l0 and stiffness x. What work must be performed to slowly get this system going and reaching the angular velocity ω?
Ans. Let the deformation in the spring be Δl, when the rod AB has attained the angular velocity ω.
From the second law of motion in projection form Fn = mwn .
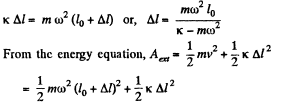
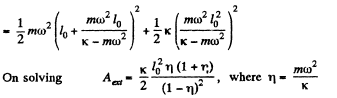
Q. 143. A pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration wc of the centre of inertia of this system.
Ans. We know that acceleration of centre of mass of the system is given by the expression.
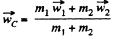
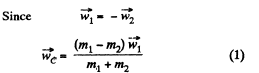
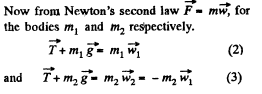
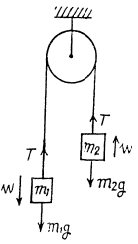
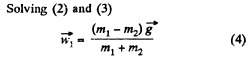
Thus from (1), (2) and (4),
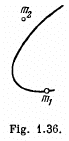
Q. 144. Two interacting particles form a closed system whose centre of inertia is at rest. Fig. 1.36 illustrates the positions of both particles at a certain moment and the trajectory of the particle of mass m1. Draw the trajectory of the particle of mass m2 if m2 = m1/2.
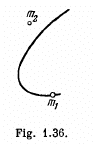
Ans. As the closed system consisting two particles m 1 and of m2 is initially at rest the C.M. of the system will remain at rest. Further as m2 = m1/2, the C.M. of the system divides the line joining m1 and m2 at all the moments of time in the ratio 1 : 2. In addition to it the total linear momentum of the system at all the times is zero. So, 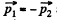 and therefore the velocities of m1 and m2 are also directed in opposite sense. Bearing in mind all these thing, the sought trajectory is as shown in the figure.
and therefore the velocities of m1 and m2 are also directed in opposite sense. Bearing in mind all these thing, the sought trajectory is as shown in the figure.
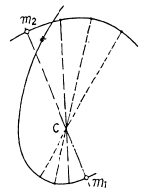
Q. 145. A closed chain A of mass m = 0.36 kg is attached to a vertical rotating shaft by means of a thread (Fig. 1.37), and rotates with a constant angular velocity ω = 35 rad/s. The thread forms an angle 0 = 45° with the vertical. Find the distance between the chain's centre of gravity and the rotation axis, and the tension of the thread.
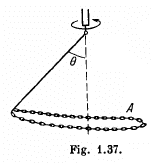
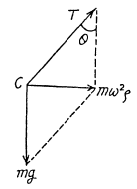
Ans. First of all, it is clear that the chain does not move in the vertical direction during the uniform rotation. This means that the vertical component of the tension T balances gravity. As for the horizontal component of the tension T, it is constant in magnitude and permanently directed toward the rotation axis. It follows from this that the C.M. of the chain, the point C, travels along horizontal circle of radius p (say). Therefore we have,
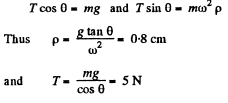
Q. 146. A round cone A of mass m = 3.2 kg and halfangle α = 10° rolls uniformly and without slipping along a round conical surface B so that its apex O remains stationary (Fig. 1.38). The centre of gravity of the cone A is at the same level as the point O and at a distance l = 17 cm from it. The cone's axis moves with angular velocity ω. Find:
(a) the static friction force acting on the cone A, if ω = 1.0 rad/s;
(b) at what values of ω the cone A will roll without sliding, if the coefficient of friction between the surfaces is equal to k = 0.25.
Ans. (a) Let us draw free body diagram and write Newton's second law in terms of projection along vertical and horizontal direction respectively.
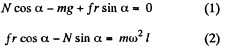
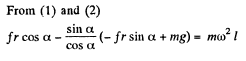
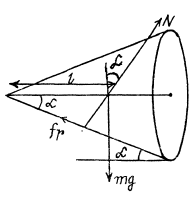
So, 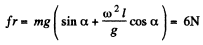 (3)
(3)
(b) For rolling, without sliding,
fr < kN
but, N = mg cos α - m ω2 l sin α
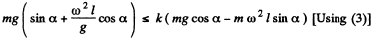
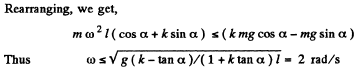
Q. 147. In the reference frame K two particles travel along the x axis, one of mass m1 with velocity v1, and the other of mass m2 with velocity v2. Find:
(a) the velocity V of the reference frame K' in which the cumulative kinetic energy of these particles is minimum;
(b) the cumulative kinetic energy of these particles in the K' frame.
Ans. (a) Total kinetic energy in frame K ' is
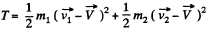
This is minimum with respect to variation in 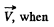 when
when
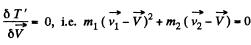
or 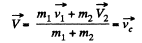
Hence, it is the frame of C.M. in which kinetic energy of a system is minimum.
(b) Linear momentum of the particle 1 in the K ' or C frame
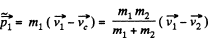
or, 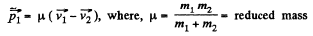
Similarly, 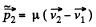
So, 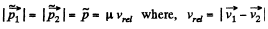 (3)
(3)
Now the total kinetic energy of the system in the C frame is
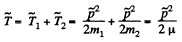
Hence 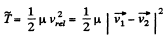
Q. 148. The reference frame, in which the centre of inertia of a given system of particles is at rest, translates with a velocity V relative to an inertial reference frame K. The mass of the system of particles equals m, and the total energy of the system in the frame of the centre of inertia is equal to 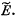 Find the total energy E of this system of particles in the reference frame K.
Find the total energy E of this system of particles in the reference frame K.
Ans. To find the relationship between the values of the mechanical eneigy of a system in the K and C reference frames, let us begin with the kinetic eneigy T of the system. The velocity of the /-th particle in the K frame may be represented as 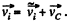 Now we can write
Now we can write
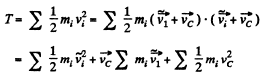
Since in the C frame 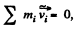 the previous expression takes the form
the previous expression takes the form
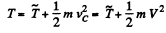 (since according to the problem vc = V) (1)
(since according to the problem vc = V) (1)
Since the internal potential eneigy U of a system depends only on its configuration, the magnitude U is the same in all refrence frames. Adding U to the left and right hand sides of Eq. (1), we obtain the sought relationship
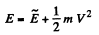
Q. 149. Two small discs of masses m1 and m2 interconnected by a weightless spring rest on a smooth horizontal plane. The discs are set in motion with initial velocities v1 and v2 whose directions are mutually perpendicular and lie in a horizontal plane. Find the total 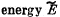 of this system in the frame of the centre of inertia.
of this system in the frame of the centre of inertia.
Ans. As initially 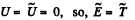
From the solution of 1.147 (b)
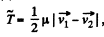
As 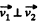
Thus 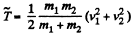
Q. 150. A system consists of two small spheres of masses m1 and m2 interconnected by a weightless spring. At the moment t = 0 the spheres are set in motion with the initial velocities v1 and v2 after which the system starts moving in the Earth's uniform gravitational field. Neglecting the air drag, find the time dependence of the total momentum of this system in the process of motion and of the radius vector of its centre of inertia relative to the initial position of the centre.
Ans. Velocity of masses m1 and m2, after t seconds are respectively.
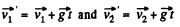
Hence the final momentum of the system,
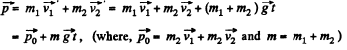
And radius vector,
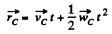
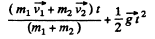

Q. 151. Two bars of masses m1 and m2 connected by a weightless spring of stiffness x (Fig. 1.39) rest on a smooth horizontal plane. Bar 2 is shifted a small distance x to the left and then released. Find the velocity of the centre of inertia of the system after bar 1 breaks off the wall.
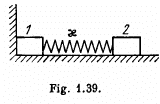
Ans. After releasing the bar 2 acquires the velocity v2, obtained by the energy, conservation :
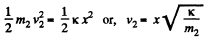 (1)
(1)
Thus the sought velocity of C.M.
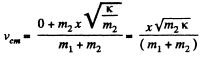
Q. 152. Two bars connected by a weightless spring of stiffness x and length (in the non-deformed state) l0 rest on a horizontal plane. A constant horizontal force F starts acting on one of the bars as shown in Fig. 1.40. Find the maximum and minimum distances between the bars during the subsequent motion of the system, if the masses of the bars are:
(a) equal;
(b) equal to m1 and m2, and the force F is applied to the bar of mass m2.
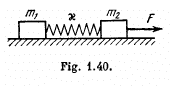
Ans. Let us consider both blocks and spring as the physical system. The centre of mass of the system moves with acceleration 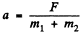 towards right Let us work in the frame of centre of mass. As this frame is a non-inertial frame (accelerated with respect to the ground) we have to apply a pseudo force m1 a towards left on the block m1 and m2 a towards left on the block m2
towards right Let us work in the frame of centre of mass. As this frame is a non-inertial frame (accelerated with respect to the ground) we have to apply a pseudo force m1 a towards left on the block m1 and m2 a towards left on the block m2
As the center of mass is at rest in this frame, the blocks move in opposite directions and come to instantaneous rest at some instant. The elongation of the spring will be maximum or minimum at this instant. Assume that the block m1 is displaced by the distance x1 and the block m2 through a distance x2 from the initial positions.
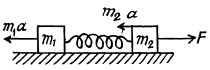
From the eneigy equation in the frame of C.M.
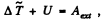
(where Aext also includes the work done by the pseudo forces)
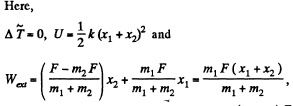
or, 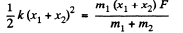
So, 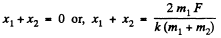
Hence the maximum separation between the blocks equals 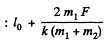
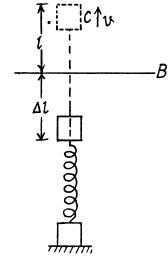
Q. 153. A system consists of two identical cubes, each of mass m, linked together by the compressed weightless spring of stiffness x (Fig. 1.41). The cubes are also connected by a thread which is burned through at a certain moment. Find:
(a) at what values of Δl, the initial compression of the spring, the lower cube will bounce up after the thread has been burned through:
(b) to what height h the centre of gravity of this system will rise if the initial compression of the spring Δl = 7 mg/x.
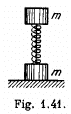
Ans. (a) The initial compression in the spring Δl must be such that after burning of the thread, the upper cube rises to a height that produces a tension in the spring that is atleast equal to the weight of the lower cube. Actually, the spring will first go from its compressed state to its natural length and then get elongated beyond this natural length. Let / be the maximum elongation produced under these circumstances.
Then
kl = mg (1)
Now, from energy conservation,
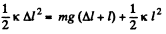 (2)
(2)
(Because at maximum elongation of the spring, the speed of upper cube becomes zero) From (1) and (2),
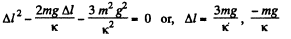
Therefore, acceptable solution of Δl equals 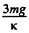
(b) Let v the velocity of upper cube at the position (say, at C) when the lower block breaks off the floor, then from energy conservation.
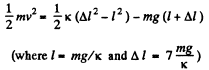
or, 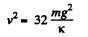 (2)
(2)
At the position C, the velocity of CM ; 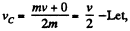 the C.M. of the system (spring + two cubes) further rises up to Δ yC2.
the C.M. of the system (spring + two cubes) further rises up to Δ yC2.
Now, from energy conservation,
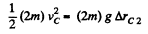
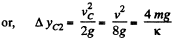
But, uptil position C, the C.M. of the system has already elevated by,
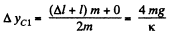
Hence, the net displacement of the C.M. of the system, in upward direction
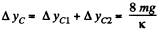
Q. 154. Two identical buggies 1 and 2 with one man in each move without friction due to inertia along the parallel rails toward each other. When the buggies get opposite each other, the men exchange their places by jumping in the direc- tion perpendicular to the motion direction. As a consequence, buggy 1 stops and buggy 2 keeps moving in the same direction, with its velocity becoming equal to v. Find the initial velocities of the buggies v1 and v2 if the mass of each buggy (without a man) equals M and the mass of each man m.
Ans. Due to ejection of mass from a moving system (which moves due to inertia) in a direction perpendicular to it, the velocity of moving system does not change. The momentum change being adjusted by the forces on the rails. Hence in our problem velocities of buggies change only due to the entrance of the man coming from the other buggy. From the
Solving (1) and (2), we get
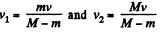
As 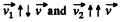
So, 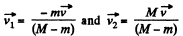
Q. 155. Two identical buggies move one after the other due to inertia (without friction) with the same velocity v0. A man of mass in rides the rear buggy. At a certain moment the man jumps into the front buggy with a velocity u relative to his buggy. Knowing that the mass of each buggy is equal to M, find the velocities with which the buggies will move after that.
Ans. From momentum conservation, for the system “rear buggy with man”
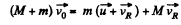 (1)
(1)
From momentum conservation, for the system (front buggy + man coming from rear buggy)
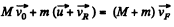
So, 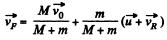
Putting the value of 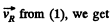
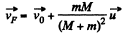
Q. 156. Two men, each of mass m, stand on the edge of a stationary buggy of mass M. Assuming the friction to be negligible, find the velocity of the buggy after both men jump off with the same horizontal velocity u relative to the buggy: (1) simultaneously; (2) one after the other. In what case will the velocity of the buggy be greater and how many times?
Ans. (i) 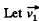 be the velocity of the buggy after both man jump off simultaneously. For the closed system (two men + buggy), from the conservation of linear momentum,
be the velocity of the buggy after both man jump off simultaneously. For the closed system (two men + buggy), from the conservation of linear momentum,
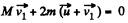
or, 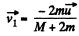 (1)
(1)
(ii) 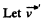 be the velocity of buggy with man, when one man jump off the buggy. For the closed system (buggy with one man + other man) from the conservation of linear momentum :
be the velocity of buggy with man, when one man jump off the buggy. For the closed system (buggy with one man + other man) from the conservation of linear momentum :
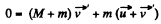 (2)
(2)
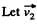 be the sought velocity of the buggy when the second man jump off the buggy; then from conservation of linear momentum of the system (buggy + one man) :
be the sought velocity of the buggy when the second man jump off the buggy; then from conservation of linear momentum of the system (buggy + one man) :
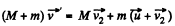 (3)
(3)
Solving equations (2) and (3) we get
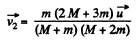 (4)
(4)
From (1) and (4)
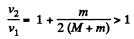
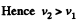
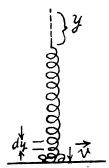
Q. 157. A chain hangs on a thread and touches the surface of a table by its lower end. Show that after the thread has been burned through, the force exerted on the table by the falling part of the chain at any moment is twice as great as the force of pressure exerted by the part already resting on the table.
Ans. The descending part of the chain is in free fall, it has speed 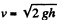 at the instant, all its points bave descended a distance y. The length of Ihe chain which lands on the floor during Ihe differential time interval dt following this instant is vdt.
at the instant, all its points bave descended a distance y. The length of Ihe chain which lands on the floor during Ihe differential time interval dt following this instant is vdt.
For the incoming chain element on the floor :
From 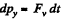 (where y - ax is is directed down)
(where y - ax is is directed down)
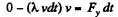
or 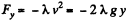
Hence, the force exerted on the falling chain equals λv2 and is directed upward. Therefore from third law the force exerted by the falling chain on the table at the same instant of time becomes λv2 and is directed downward.
Since a length of chain of weight (λyg) already lies on the table the total force on the floor is (2λyg) + (λyg) = (3λyg) or the weight of a length 3y of chain.
Q. 158. A steel ball of mass m = 50 g falls from the height h = 1.0 m on the horizontal surface of a massive slab. Find the cumulative momentum that the ball imparts to the slab after numerous bounces, if every impact decreases the velocity of the ball η = 1.25 times.
Ans. Velocity of the ball, with which it hits the slab, 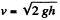
After first impact, v' = ev (upward) but according to the problem 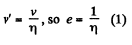 and momentum, imparted to the slab,
and momentum, imparted to the slab,
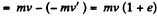
Similarly, velocity of the ball after second impact,
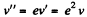
And momentum imparted 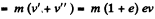
Again, momentum imparted during third impact,
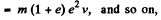
Hence, net momentum, imparted 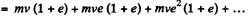
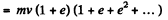
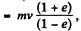 (from summation of G.P.)
(from summation of G.P.)
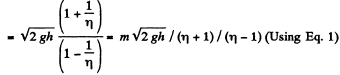
= 0.2 kg m/s. (On substitution)
Q. 159. A raft of mass M with a man of mass m aboard stays motionless on the surface of a lake. The man moves a distance 1' relative to the raft with velocity v'(t) and then stops. Assuming the water resistance to be negligible, find:
(a) the displacement of the raft 1 relative to the shore;
(b) the horizontal component of the force with which the man acted on the raft during the motion.
Ans. (a) Since the resistance of water is negligibly small, the resultant of all external forces acting on the system “a man and a raft” is equal to zero. This means that the position of the C.M. of the given system does not change in the process of motion.
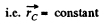
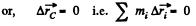
or, 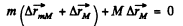
Thus, 
(b) As net external force on “man-raft” system is equal to zero, therefore the momentum of this system does not change,
So, 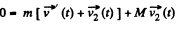
or, 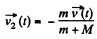 (1)
(1)
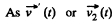 is along horizontal direction, thus the sought force on the raft
is along horizontal direction, thus the sought force on the raft
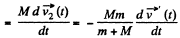
Note : we may get the result of part (a), if we integrate Eq. (1) over the time of motion of man or raft.
Q. 160. A stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance 1' with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement 1 of the centre of inertia of this system.
Ans. In the refrence frame fixed to the pulley axis the location of C.M. of the given system is described by the radius vector
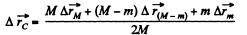
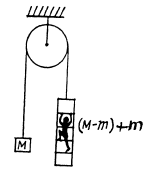
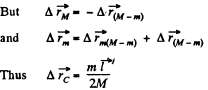
Note : one may also solve this problem using momentum conservation
FAQs on Irodov Solutions: Laws of Conservation of Energy, Momentum & Angular Momentum - 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the law of conservation of energy? |  |
| 2. How is the law of conservation of momentum applied in physics? |  |
| 3. What is the significance of the law of conservation of angular momentum? |  |
| 4. Can energy be converted from one form to another? |  |
| 5. How does the law of conservation of momentum relate to Newton's third law of motion? |  |
















