Irodov Solutions: Mechanical Oscillations- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 1. A point oscillates along the x axis according to the law x = a cos (ωt — n/4). Draw the approximate plots
(a) of displacement x, velocity projection vx, and acceleration projection wx as functions of time t;
(b) velocity projection vx and acceleration projection wx as functions of the coordinate x.
Ans. 1. (a) Given, x =
So
On-the basis of obtained expressions plots x(t) , vx(t) and wx(t) can be drawn as shown in the answersheet, (of the problem book ).
(b) From Eqn (1)
(2)
But from the law x = a cos (ωt - π/4) , so, x 2 = a2 cos2 (ωt - π/4)
or, cos (ωt - π/4) - X2/ = 2 or sin2 (ωt - 3t/4) = (3)
Using (3) in (2), (4)
Again from Eqn (4), wx = -aω2cos (ωt - π/4) = -ω2x
Q. 2. A point moves along the x axis according to the law x = a sin2(ωt — π/4). Find: (a) the amplitude and period of oscillations; draw the plot x (t); (b) the velocity projection vx as a function of the coordinate x; draw the plot vx (x).
Ans. 2. (a) From the motion law of the particle
(1)
Now compairing this equation with the general equation of harmonic oscillations : X - A sin(ωot+a) Amplitude, A = a/2 and angular frequency, ω0 - 2ω.
Thus the period of one full oscillation,
(b) Differentiating Eqn (1) w.r.t. time
Plot of vx (x) is as shown in the answersheet.
Q. 3.A particle performs harmonic oscillations along the x axis about the equilibrium position x = 0. The oscillation frequency is ω = 4.00 s-1 . At a certain moment of time the particle has a coor- dinate xo = 25.0 cm and its velocity is equal to vx0 = 100 cm/s. Find the coordinate x and the velocity vx of the particle t = 2.40s after that moment.
Ans. 3 Let the general equation of S.H.M. be
h = a cos (ωt + α)
So, vx = - a ω sin (ωt + α)
Let us assume that at t = 0 , x = h0 and
Thus from Eqns (1) and (2) for t = 0, h0 = a cos α, and = - a ωsin α
Putting all the given numerical values, we get :
x = - 29 cm and vx = - 81 cm/s
Q. 4.Find the angular frequency and the amplitude of harmonic oscillations of a particle if at distances x1 and x2 from the equilibrium position its velocity equals v1 a nd v2 respectively.
Ans. From the Eqn
Solving these Eqns simultaneously, we get
Q. 5. A point performs harmonic oscillations along a straight line with a period T = 0.60 s and an amplitude a = 10.0 cm. Find the mean velocity of the point averaged over the time interval during which it travels a distance a/2, starting from
(a) the extreme position;
(b) the equilibrium position.
Ans. (a) When a particle starts from an extreme position, it is useful to write the motion law as x = a cos ωt (1)
(However x is the displacement from the equlibrium position)
It tx be the time to cover the distence a/2 then from (1)
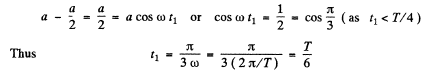
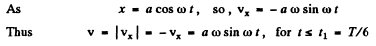
Hence sought mean velocity
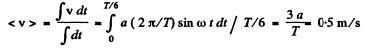
(b) In this case, it is easier to write the motion law in the form :
x = a sin ωt (2)
If t2 be the time to cover the distance a/2, then from Eqn (2)
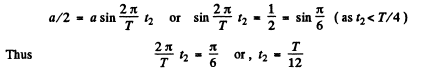
Differentiating Eqn (2) w.r.t time, we get
Hence the sought mean velocity
Q. 6. At the moment t = 0 a point starts oscillating along the x axis according to the law x = a sin ωt. Find:
(a) the mean value of its velocity vector projection (vs);
(b) the modulus of the mean velocity vector |(v)| ;
(c) the mean value of the velocity modulus (v) averaged over 3/8 of the period after the start.
Ans. (a) As x = a sin ωt so, vx = aω cos ωt
(b) In accordance with the problem
(c) We have got, vx = a ω cos ωt
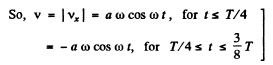
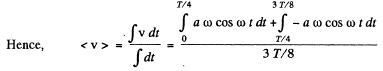
Using ω = 2 ω/T , and on evaluating the integral we get
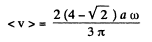
Q. 7. A particle moves along the x axis according to the law x = a cos ωt. Find the distance that the particle covers during the time interval from t = 0 to t.
Ans. From the motion law, x = a cos ωt„ it is obvious that the time taken to cover the distance equal to the amplitude (a), starting from extreme position equals T/4.
Now one can write
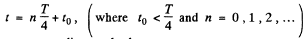
As the particle moves according to the law, x .= a cos ωt, so at n = 1,3,5 ... or for odd n values it passes through the mean positon and for even numbers of n it comes to an extreme position (if t0 = 0).
Case (1) when n is an odd number : In this case, from the equation
x = x a sin ωt, if the t is counted from nT/4 and the distance covered in the time interval to be comes
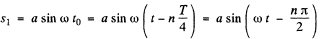
Thus the sought distance covered for odd n is
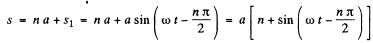
Case (2), when n is even, In this case from the equation x = a cos ωt, the distance covered ( s2 ) in the interval t0, is given by
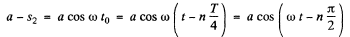
or 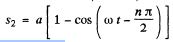
Hence the sought distance for n is even
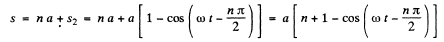
In general
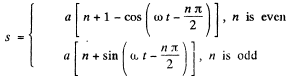
Q. 8. At the moment t = 0 a particle starts moving along the x axis so that its velocity projection varies as vx = 35 cos πt cm/s, where t is expressed in seconds. Find the distance that this particle covers during t = 2.80 s after the start.
Ans. Obviously the motion law is of the from, x = a shoot, and vx = ω a cos ωt.
Comparing vx - ω a cos ωt with vx - 35 cos πt , we get
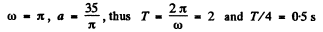
Now we can write
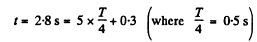
As n = 5 is odd, like (4 = 7), we have to basically find the distance covered by the particle starting from the extreme position in the time interval 0 = 3 s.
Thus from the Eqn.
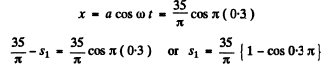
Hence the sought distance

Q. 9. A particle performs harmonic oscillations along the x axis according to the law x = a cos ωt. Assuming the probability P of the particle to fall within an interval from —a to +a to be equal to unity, find how the probability density dP/dx depends on x. Here dP denotes the probability of the particle falling within an interval from x to x dx. Plot dP/dx as a function of x.
Ans. As the motion is periodic the particle repeatedly passes through any given region in the range - a ≤ x ≤ a.
The probability that it lies in the range (x, x + dx) is defined as the fraction
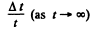 where Δt is the time that the particle lies in the range (x, x + dx) out of the total time t. Because of periodicity this is
where Δt is the time that the particle lies in the range (x, x + dx) out of the total time t. Because of periodicity this is
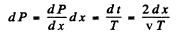
where the factor 2 is needed to take account of the fact that the particle is in the range ( x , x + d x ) during both up and down phases of its motion. Now in a harmonic oscillator.
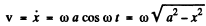
Thus since ωT = 2 π ( T is the time period)
We get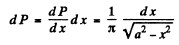
Note that 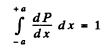
so 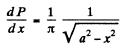
Q. 10. Using graphical means, find an amplitude a of oscillations resulting from the superposition of the following oscillations of the same direction:
(a) x1 =3 .0 cos (ωt -1- π/3), x2 =8 .0 sin (ωt + π/6);
(b) x1 = 3.0 cos ωt, x2 = 5.0 cos (ωt+ π/4), x3 =6 .0 sin ωt.
Ans. (a) We take a graph paper and choose an axis (X - axis) and an origin. Draw a vector of magnitude 3 inclined at an angle π/3 with the X -axis. Draw another vector of magnitude 8 inclined at an angle - π/3( Since sin (ωt+ π/ 6 ) » cos (ωt- π/ 3 )) with the X - axis. The magnitude of the resultant of both these vectors (drawn from the origin) obtained using parallelogram law is the resultant, amplitude.
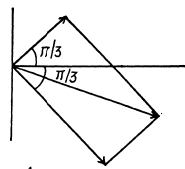
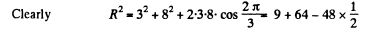
Thus R = R7 units
(b) One can follow the same graphical method here but the result can be obtained more quickly by breaking into sines and cosines and adding :
Resultant
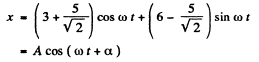
Then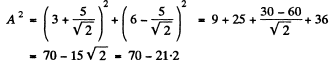
So, A = 6-985 = 7 units
Note- In using graphical method convert all oscillations to either sines or cosines but do not use both.
FAQs on Irodov Solutions: Mechanical Oscillations- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is mechanical oscillation? |  |
| 2. What are the different types of mechanical oscillations? |  |
| 3. How is simple harmonic motion related to mechanical oscillations? |  |
| 4. What factors affect the frequency of mechanical oscillations? |  |
| 5. How can mechanical oscillations be used in practical applications? |  |






















