Irodov Solutions: Mechanical Oscillations- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 11. A point participates simultaneously in two harmonic oscillations of the same direction: x1 = a cos ωt and
x2 = a cos 2ωt.
Find the maximum velocity of the point.
Ans. Given , x1 = a cos ωt and x 2 = a cos 2 ωt
so, the net displacement,
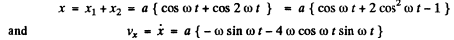
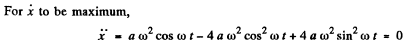
Solving for acceptable value
cos ωt = 0.644
thus sin ωt = 0.765
and 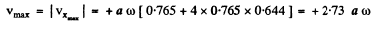
Q. 12. The superposition of two harmonic oscillations of the same direction results in the oscillation of a point according to the law x = a cos 2.1t cos 50.0t, where t is expressed in seconds. Find the angular frequencies of the constituent oscillations and the period with which they beat.
Ans. We write :
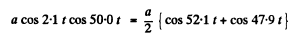
Thus the angular frequencies of constituent oscillations are
52.1 s-1 and 47.9 s-1
To get the beat period note that the variable amplitude a cos 2.1t becomes maximum (positive or negative), when
2.1t = nπ Thus the interval between two maxima is
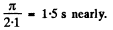
Q. 13. A point A oscillates according to a certain harmonic law in the reference frame K' which in its turn performs harmonic oscillations relative to the reference frame K. Both oscillations occur along the same direction. When the K' frame oscillates at the frequency 20 or 24 Hz, the beat frequency of the point A in the K frame turns 167 out to be equal to v. At what frequency of oscillation of the frame K' will the beat frequency of the point A become equal to 2v?
Ans. If the frequency of A with respect to K' is v0 and K ' oscillates with frequency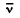 with respect to K, the beat frequency of the point A in the .K-frame will be v when
with respect to K, the beat frequency of the point A in the .K-frame will be v when
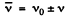
In the present case 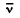 = 20 or 24.
= 20 or 24.
This means v0 - 22. & v - 2
Thus beats of 2v = 4 will be heard when 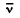 = 26 or 18 .
= 26 or 18 .
Q. 14. A point moves in the plane xy according to the law x = a sin ωt, y = b cos ωt, where a, b, and ω are positive constants. Find:
(a) the trajectory equation y (x) of the point and the direction of its motion along this trajectory;
(b) the acceleration ω of the point as a function of its radius vector r relative to the origin of coordinates.
Ans. (a) From the Eqn : x = a sin ωt
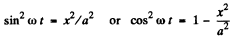 (1)
(1)
And from the equation :
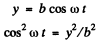 (2)
(2)
From Eqns (1) and (2), we get :
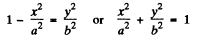
which is the standard equation of the ellipse shown in the figure, we observe that,
at t = 0 , x = 0 and y = b
and at
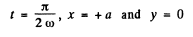
Thus we observe that at t = 0, the point is at point 1 (Fig.) and at the following moments, the co-ordinate y diminishes and x becomes positive. Consequently the motion is clockwise.
(b) As x = d sin ωt and y=b cos ωt
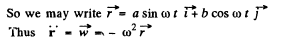
Q. 15. Find the trajectory equation y (x) of a point if it moves according to the following laws:
(a) x = a sin ωt, y = a sin 2ωt;
(b) x = a sin cot, y = a cos 2ωt.
Plot these trajectories.
Ans. (a) From the Eqn. : x = a sin ωt , we have
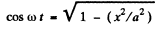
and from the Eqn. :y = a sin 2 ωt
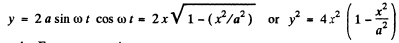
(b) From the Eqn. : x = a sin ωt
sin2 ωt = x 2/a 2
Fromy = a cos 2 ωt
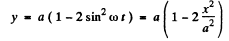
For tiie plots see the plots of answersheet of tlve problem book.
Q. 16. A particle of mass m is located in a unidimensional potential field where the potential energy of the particle depends on the coordinate x as U (x) = U0 (1 — cos ax); U0 and a are constants. Find the period of small oscillations that the particle performs about the equilibrium position.
Ans. As U ( x ) = U0 ( 1 - cos ax)
So, 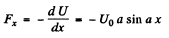 (1)
(1)
or, Fx = - U0 a a x (because for small angle o f oscillations sin a x = a x )
or, 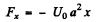 (1)
(1)
But we know 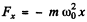 , for small oscillation
, for small oscillation
Thus 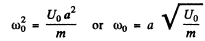
Hence the sought time period
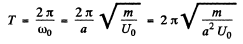
Q. 17. Solve the foregoing problem if the potential energy has the form U (x) = alx2 — blx, where a and b are positive constants.
Ans. 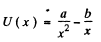
then the equilibrium position is x = x0 when U" (x0) = 0
or, 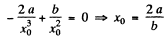
Now write : x = x0+ y
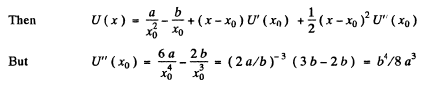
So finally : 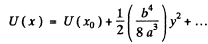
We neglect remaining terms for small oscillations and compare with the P.E. for a harmonic, oscillator :
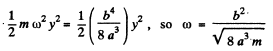
Thus 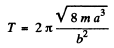
Note : Equilibrium position is generally a minimum of the potential energy. Then U' ( xo ) - 0 , U" ( x0 ) > 0 . The equilibrium position can in principle be a maxim um but then U" (xo) < 0 and the frequency of oscillations about this equilibrium position will be imaginary.
The answer given in the book is incorrect both numerically and dimensionally.
Q. 18. Find the period of small oscillations in a vertical plane performed by a ball of mass m = 40 g fixed at the middle of a horizontally stretched string l = 1.0 m in length. The tension of the string is assumed to be constant and equal to F = 10 N.
Ans. Let us locate and depict the forces acting on the ball at the position when it is at a distance x down from the undeformed position of the string.
At this position, the unbalanced downward force on the ball
= mg - 2.F sinθ

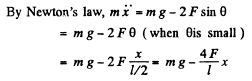
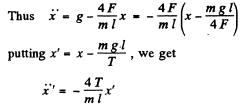
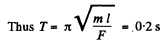
Q. 19. Determine the period of small oscillations of a mathematical pendulum, that is a ball suspended by a thread l = 20 cm in length, if it is located in a liquid whose density is η = 3.0 times less than that of the ball. The resistance of the liquid is to be neglected.
Ans. Let us depict the forces acting on the oscillating ball at an arbitraty angular position 0. (Fig.), relative to equilibrium position where FB is the force of buoyancy. For the ball from the equation :
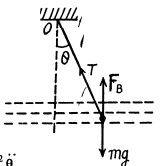
Nz - Iβz (where w e have taken the positive sense of Z axis in the direction of angular velocity i.e. 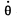 of the ball and passes through the point of suspension of the pendulum O ), we get :
of the ball and passes through the point of suspension of the pendulum O ), we get :
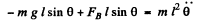 (1)
(1)
Using 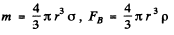 and sin θ = θ for small θ, in Eqn (1), we get :
and sin θ = θ for small θ, in Eqn (1), we get :
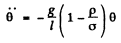
Thus the sought time period

Hence 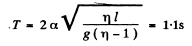
Q. 20. A ball is suspended by a thread of length l at the point 0 on the wall, forming a small angle α with the vertical (Fig. 4.1). Then

the thread with the ball was deviated through a small angle β(β > α) and set free. Assuming the collision of the ball against the wall to be perfectly elastic, find the oscillation period of such a pendulum.
Ans. Obviously for small p the ball execute part of S.H.M. Due to the perfectly elastic collision the velocity of ball simply reversed. As the ball is in S.H.M. (|θ| < α on the left)its motion law in differential from can be written as
 (1)
(1)
If we assume that the ball is released from the extreme position, θ = β at t = 0, the solution of differential equation would be taken in the form
 (2)
(2)
If t ' be the time taken by the ball to go from the extreme position θ = β to the wall i.e. θ = - α , then Eqn. (2) can be rewritten as
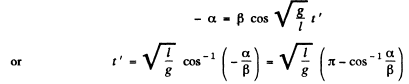
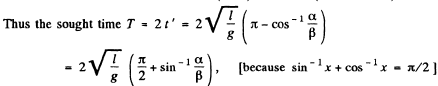
FAQs on Irodov Solutions: Mechanical Oscillations- 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the equation of motion for a mechanical oscillator? |  |
| 2. How is the time period of a mechanical oscillator related to its mass and spring constant? |  |
| 3. What is the amplitude of a mechanical oscillator? |  |
| 4. What is the relationship between the frequency and angular frequency of a mechanical oscillator? |  |
| 5. How does damping affect the motion of a mechanical oscillator? |  |





















