Irodov Solutions: Elastic Deformations of a Solid Body | Physics Class 11 - NEET PDF Download
Q. 290. What pressure has to be applied to the ends of a steel cylinder to keep its length constant on raising its temperature by 100°C?
Solution. 290. Variation of length with temperature is given by

But 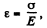
Thus σ = αΔtE, which is the sought stress of pressure.
Putting the value of a and E from Appendix and taking Δt = 100°C, we get
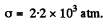
Q. 291. What internal pressure (in the absence of an external pressure) can be sustained
(a) by a glass tube;
(b) by a glass spherical flask, if in both cases the wall thickness is equal to Δr = 1.0 mm and the radius of the tube and the flask equals r = 25 mm?
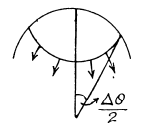
Solution. 291. (a) Consider a transverse section of the tube and concentrate on an element which subtends an angle Δφ at the centre. The forces acting on a portion of length A/ on the element are
(1) tensile forces side ways of magnitude σΔrΔl.
The resultant of these is
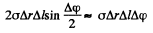
radially towards the cente.
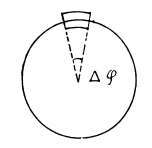
(2) The force due to fluid pressure 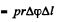 Since these balance, we get
Since these balance, we get 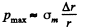 where σm is the maximum tensile force. Putting the values we get atmos.
where σm is the maximum tensile force. Putting the values we get atmos. 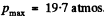
(b) Consider an element of area 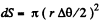 about z -a x is chosen arbitrarily. There are tangential tensile forces all around the ring of the cap. Their resultant is
about z -a x is chosen arbitrarily. There are tangential tensile forces all around the ring of the cap. Their resultant is
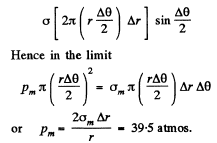
Q. 292. A horizontally oriented copper rod of length l = 1.0 m is rotated about a vertical axis passing through its middle. What is the number of rps at which this rod ruptures?
Solution. 292. Let us consider an element of rod at a distance x from its rotation axis (Fig.). From Newton’s second law in projection form directed towards the rotation axis

On integrating
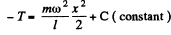
But 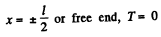
Thus 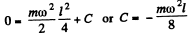
Hence 
Thus 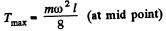

Condition renuired for the. problem
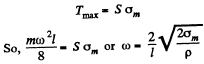
Hence the sought number of r p s

Q. 293. A ring of radius r = 25 cm made of lead wire is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring. What is the number of rps at which the ring ruptures?
Solution. 293. Let us consider an element of the ring (Fig.). From Newton’s law Fn = mwn for this element, we get,
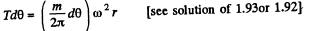
So, 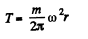
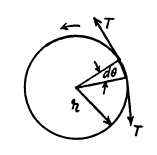
Condition for the problem is :
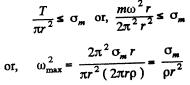
Thus sought number of rps
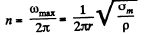
Using the table of appendices n = 23rps
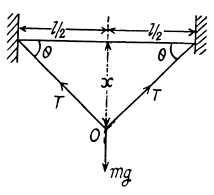
Q. 294. A steel wire of diameter d = 1.0 mm is stretched horizontally between two clamps located at the distance l = 2.0 m from each other. A weight of mass m = 0.25 kg is suspended from the midpoint O of the wire. What will the resulting descent of the point O be in centimetres?
Solution. 294. Let the point O desend by the distance x (Fig.). From the condition of equilibrium of point O.
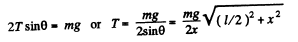 (1)
(1)
Now, 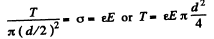 (2)
(2)
(σ here is stress and ε is strain.)
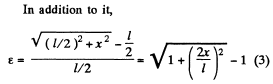
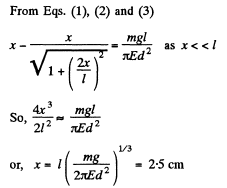
Q. 295. A uniform elastic plank moves over a smooth horizontal plane due to a constant force F0 distributed uniformly over the end face. The surface of the end face is equal to S, and Young's modulus of the material to E. Find the compressive strain of the plank in the direction of the acting force.
Solution. 295. Let us consider an element of the rod at a distance x from the free end (Fig.). For the considered element ‘T - T’ are internal restoring forces which produce elongation and dT provides the acceleration to the element. For the element from Newton’s law :
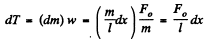
As free end has zero tension, on integrating the above expression,
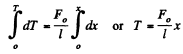
Elongation in the considered element of lenght dx :
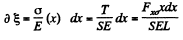
Thus total elengation 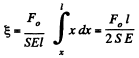
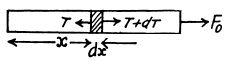
Hence the sought strain
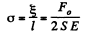
Q. 296. A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
Solution. 296. Let us consider an element of the rod at a distance r from it’s rotation axis. As the element rotates in a horizontal circle of radius r, we have from Newton’s second law in projection form directed toward the axis of rotation :
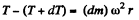
or, 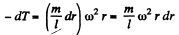
At the free end tension becomes zero. Integrating the above experession we get, thus
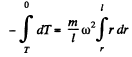
Thus 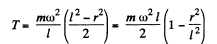
Elongation in elemental length dr is given by :
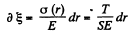
(where S is the cross sectional area of the rod and T is the tension in the rod at the considered element)

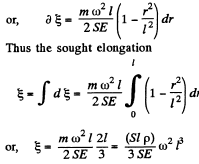
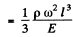 (where p is the density of the copper.)
(where p is the density of the copper.)
Q. 297. A solid copper cylinder of length l = 65 cm is placed on a horizontal surface and subjected to a vertical compressive force F = 1000 N directed downward and distributed uniformly over the end face. What will be the resulting change of the volume of the cylinder in cubic millimetres?
Solution. 297. Volume of a solid cylinder
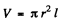
So, 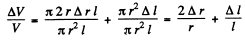 (1)
(1)
But longitudinal strain Δl/l and accompanying lateral strain Δ r/r are related as
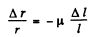 (2)
(2)
Using (2) in (1), we get :
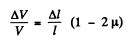 (3)
(3)
But 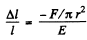
(Because the increment in the length of cylinder Δl is negative)
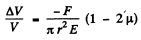
Thus, 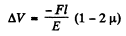
Negative sign means that the volume of the cylinder has decreased.
Q. 298. A copper rod of length l is suspended from the ceiling by one of its ends. Find:
(a) the elongation Δl of the rod due to its own weight;
(b) the relative increment of its volume ΔVIV.
Solution. 298. (a) As free end has zero tension, thus the tension in the rod at a vestical distance y from its lower end
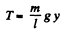
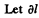 be the elongation of the element of length dy, then
be the elongation of the element of length dy, then

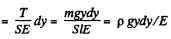 (where p is the density of the copper)
(where p is the density of the copper)
Thus the sought elongation
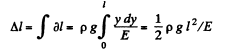 (2)
(2)
(b) If the longitudinal (tensile) strain is 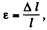 the accompanying lateral (compressive) strain is given by
the accompanying lateral (compressive) strain is given by
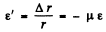 (3)
(3)
Then since 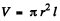 we have
we have
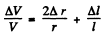
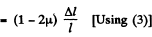
where  is given in part (a), μ is the Poisson ratio for copper.
is given in part (a), μ is the Poisson ratio for copper.
Q. 299. A bar made of material whose Young's modulus is equal to E and Poisson's ratio to μ, is subjected to the hydrostatic pressure p. Find:
(a) the fractional decrement of its volume;
(b) the relationship between the compressibility β and the elastic constants E and μ.
Solution. 299. Consider a cube of unit length before pressure is applied. The pressure acts on each face. The pressures on the opposite faces constitute a tensile stress producing longitudianl compression and lateral extension. The compressions is P/E and the lateral extension is 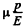
The net result is a compression 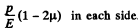
Hence 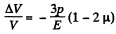 because from symmetry
because from symmetry 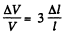
(b) Let us consider a cube under an equal compressive stress σ, acting on all its faces.
Then, 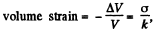 (1)
(1)
where k is the bulk modulus of elasticity.
So 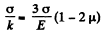
or, 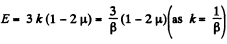
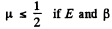 are both to remain positive.
are both to remain positive.
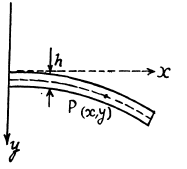
Q. 300. One end of a steel rectangular girder is embedded into a wall (Fig. 1.74). Due to gravity it sags slightly. Find the radius of curvature of the neutral layer (see the dotted line in the figure) in the vicinity of the point O if the length of the protruding section of the girder is equal to l = 6.0 m and the thickness of the girder equals h = 10 cm.

Solution. 300. A beam clamped at one end and supporting an applied load at the free end is called a cantilever. The theory of cantilevers is discussed in advanced text book on mechanics. The key result is that elastic forces in the beam generate a couple, whose moment, called the moment of resistances, balances the external bending moment due to weight of the beam, load etc. The moment of resistance, also called internal bending moment (I.B.M) is given by
I.B.M. = EI/R
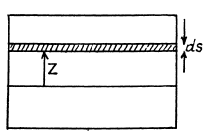
Here R is the radius of curvature of the beam at the representative point (x, y). I is called the geometrical moment of inertia
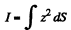
of the cross section relative to the axis passing through the netural layer which remains unstretched. (Fig.l.). The section of the beam beyond P exerts the bending moment N (x) and we have,
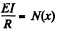
If there is no load other than that due to the weight of the beam, then

where p = density of steel. Hence, at x = 0
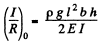
Here b = width of the beam perpendicular to paper.
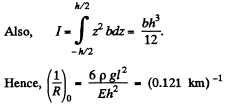
Q. 301. The bending of an elastic rod is described by the elastic curve passing through centres of gravity of rod's cross-sections. At small bendings the equation of this curve takes the form 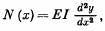
where N (x) is the bending moment of the elastic forces in the cross- section corresponding to the x coordinate, E is Young's modulus, I is the moment of inertia of the cross-section relative to the axis pass- ing through the neutral laye 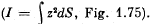
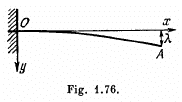
Suppose one end of a steel rod of a square cross-section with side a is embedded into a wall, the protruding section being of length l (Fig. 1.76). Assuming the mass of the rod to be negligible, find the shape of the elastic curve and the deflection of the rod X, if its end A experiences
(a) the bending moment of the couple N0;
(b) a force F oriented along the y axis
Solution. 301. We use the equation given above and use the result that when y is small
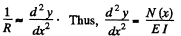
(a) Here N (x) = N0 is a constant. Then integration gives,
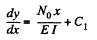
But 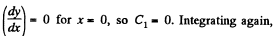

where we have used y = 0 for x = 0 to set the constant of integration at zero. This is the equation of a parabola. The sag of the free end is
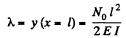
(b) In this case N (x) - F (l - x) because the load F at the extremity is balanced by a similar force at F directed upward and they constitute a couple. Then
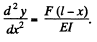
Integrating, 
As before C1 = 0. Integrating again, using y = 0 for x = 0
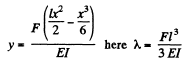
Here for a square cross section
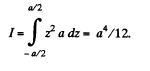
Q. 302. A steel girder of length l rests freely on two supports (Fig. 1.77). The moment of inertia of its cross-section is equal to I (see the foregoing problem). Neglecting the mass of the girder and assuming the sagging to he slight, find the deflection λ due to the force F applied to the middle of the girder.
Solution. 302. One can think of it as analogous to the previous case but with a beam of length l/2 loaded upward by a force F/2.
Thus 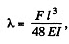
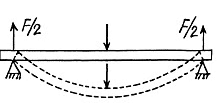
On using the last result of the previous problem.
Q. 303. The thickness of a rectangular steel girder equals h. Using the equation of Problem 1.301, find the deflection λ caused by the weight of the girder in two cases:
(a) one end of the girder is embedded into a wall with the length of the protruding section being equal to l (Fig. 1.78a);
(b) the girder of length 2l rests freely on two supports (Fig. 1.78b).
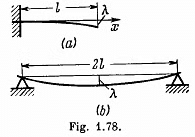
Solution. 303. (a) 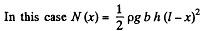 where b = width of the girder.
where b = width of the girder.
Also 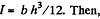
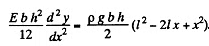
Integrating, 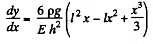
using 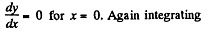
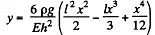
Thus 
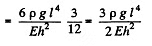
(b) As before, 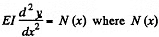 is the bending moment due to section PB.
is the bending moment due to section PB.
This bending moment is clearly
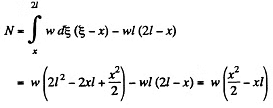
(Here w = p g b h is weight o f the beam per unit length)
Now integrating, 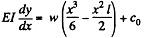
or since 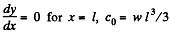
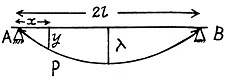 Integrating again,
Integrating again, 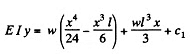
As y = 0 for x = 0, c1 = 0. From this we find
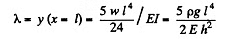
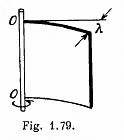
Q. 304. A steel plate of thickness h has the shape of a square whose side equals l, with h << 1. The plate is rigidly fixed to a vertical axle OO which is rotated with a constant angular acceleration 13 (Fig. 1.79). Find the deflection λ, assuming the sagging to be small.
Solution. 304. The deflection of the plate can be noticed by going to a co- rotating frame. In this frame each element of the plate experiences a pseudo force proportional to its mass. These forces have a moment which constitutes the bending moment of the problem. To calculate this moment we note that the acceleration of an element at a distance 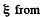 from the axis is
from the axis is 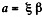 and the moment of the forces exerted by the section between x and l is
and the moment of the forces exerted by the section between x and l is
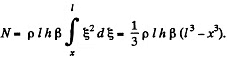
From the fundamental equation
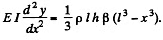
The moment of inertia 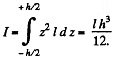
Vofe that the neutral surface (i.e. the surface which contains lines which are neither stretched nor compressed) is a vertical plane here and z is perpendicular to it.

Since 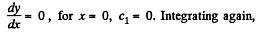
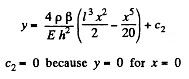
Thus 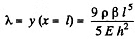
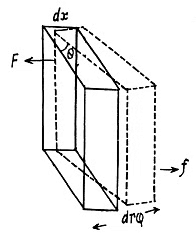
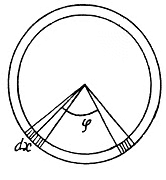
Q. 305. Determine the relationship between the torque N and the torsion angle φ for
(a) the tube whose wall thickness Δr is considerably less than the tube radius;
(b) for the solid rod of circular cross-section. Their length l, radius r, and shear modulus G are supposed to be known.
Solution. 305. (a) Consider a hollow cylinder of length l, outer radius r + Δr inner radius r, fixed at one end and twisted at the other by means of a couple of moment N. The angular displacement φ, at a distance l from the fixed end, is proportional to both l and N. Consider an element of length dx at the twisted end. It is moved by an angle φ as shown. A vertical section is also shown and the twisting of the parallelopipe of length l and area Δr dx under the action of the twisting couple can be discussed by elementary means. If f is the tangential force generated then shearing stress is f/Δr dx and this must equal
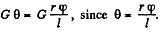
Hence , 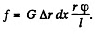
The force / has moment f r about the axis and so the total moment is

(b) For a solid cylinder we must integrate over r. Thus

Q. 306. Calculate the torque N twisting a steel tube of length l = 3.0 m through an angle φ = 2.0° about its axis, if the inside and outside diameters of the tube are equal to d1 = 30 mm and d2 = 50 mm.
Solution. 306. 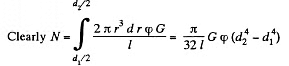
using 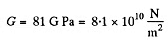
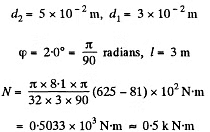
Q. 307. Find the maximum power which can be transmitted by means of a steel shaft rotating about its axis with an angular velocity ω = 120 rad/s, if its length l = 200 cm, radius r = 1.50 cm, and the permissible torsion angle φ = 2.5°.
Solution. 307. The maximum power that can be transmitted by means of a shaft rotating about its axis is clearly N ω where N is the moment of the couple producing the maximum permissible torsion, φ. Thus
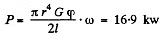
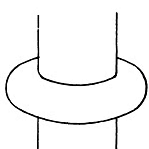
Q. 308. A uniform ring of mass m, with the outside radius r2, is fitted tightly on a shaft of radius r1. The shaft is rotated about its axis with a constant angular acceleration β. Find the moment of elastic forces in the ring as a function of the distance r from the rotation axis.
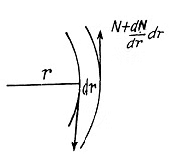
Solution. 308. Consider an elementary ring of width dr at a distant r from the axis. The part outside exerts a couple  dr on this ring while the part inside exerts a couple N in the opposite direction. We have for equilibrium
dr on this ring while the part inside exerts a couple N in the opposite direction. We have for equilibrium

where dl is the moment of inertia o f the elementary ring, β is the angular acceleration and minus sign is needed because the couple N (r) decreases, with distance vanshing at the outer radius, N (r2) = 0. Now

Thus 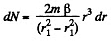
or, 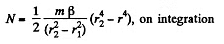
Q. 309. Find the elastic deformation energy of a steel rod of mass m = 3.1 kg stretched to a tensile strain ε = 1.0-10-3.
Solution. 309. We assume that the deformation is wholly due to external load, neglecting the effect of the weight of the rod (see next problem). Then a well known formula says,
elastic energy per unit volume
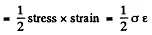
This gives 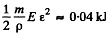 for the total deformation energy.
for the total deformation energy.
Q. 310. A steel cylindrical rod of length l and radius r is suspended by its end from the ceiling.
(a) Find the elastic deformation energy U of the rod.
(b) Define U in terms of tensile strain Δl/l of the rod.
Solution. 310. When a rod is deformed by its own weight the stress increases as one moves up, the stretching force being the weight of the portion below the element considered.
The stress on the element dx is
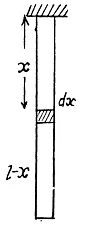
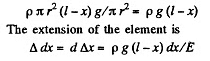
Integrating 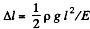 is the extension of the whole rod. The elastic energy of the element is
is the extension of the whole rod. The elastic energy of the element is

Integrating
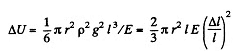
Q. 311. What work has to be performed to make a hoop out of a steel band of length l = 2.0 m, width h = 6.0 cm, and thickness δ = 2.0 mm? The process is assumed to proceed within the elasticity range of the material.
Solution. 311. The work done to make a loop out of a steel band appears as the elastic energy of the loop and may be calculated from the same.
If the length of the band is l, the radius of the loop 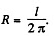 Now consider an element ABCD of the loop. The elastic energy of this element can be calculated by the same sort of arguments as used to derive the formula for internal bending moment. Consider a fibre at a distance z from the neutral surface PQ. This fibre experiences a forcep and undergoes an extension
Now consider an element ABCD of the loop. The elastic energy of this element can be calculated by the same sort of arguments as used to derive the formula for internal bending moment. Consider a fibre at a distance z from the neutral surface PQ. This fibre experiences a forcep and undergoes an extension 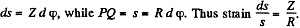 If α is the cross sectional area of the fibre, the elastic energy associated with it is
If α is the cross sectional area of the fibre, the elastic energy associated with it is
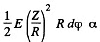
Summing over all the fibres we get
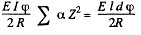
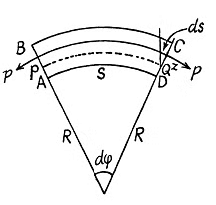
For the whole loop this gives,
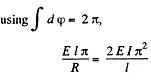
Now 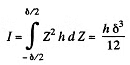
So the energy is 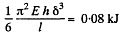
Q. 312. Find the elastic deformation energy of a steel rod whose one end is fixed and the other is twisted through an angle φ = 6.0°. The length of the rod is equal to l = 1.0 m, and the radius to r = 10 mm.
Solution. 312. When the rod is twisted through an angle θ a couple
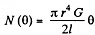 appears to resist this. Work done in twisting the rod by an angle φ is then
appears to resist this. Work done in twisting the rod by an angle φ is then
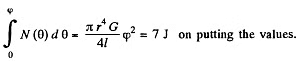
Q. 313. Find how the volume density of the elastic deformation energy is distributed in a steel rod depending on the distance r from its axis. The length of the rod is equal to l, the torsion angle to φ.
Solution. 313. The energy between radii r and r + dr is, by differentiation, 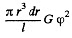
Its density is 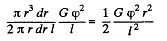
Q. 314. Find the volume density of the elastic deformation energy in fresh water at the depth of h = 1000 m.
Solution. 314. The energy density is as usual 1/2 stress x strain. Stress is the pressure p g h. Strain is β x p gh by defination of β. Thus

|
96 videos|367 docs|98 tests
|
FAQs on Irodov Solutions: Elastic Deformations of a Solid Body - Physics Class 11 - NEET
| 1. What is elastic deformation of a solid body? |  |
| 2. What causes elastic deformation in a solid body? |  |
| 3. How can we measure elastic deformation in a solid body? |  |
| 4. What is the relationship between stress and elastic deformation? |  |
| 5. What are some real-life examples of elastic deformation in solid bodies? |  |
















