Irodov Solutions: The Second Law of Thermodynamics Entropy- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 134. Find the entropy increment of v = 2.0 moles of an ideal gas whose adiabatic exponent γ = 1.30 if, as a result of a certain process, the gas volume increased α = 2.0 times while the pressure dropped β = 3.0 times.
Solution. 134.
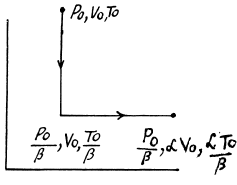
The entropy change depends on the initial and final state only so can be calculated for any process whatsoever.
We choose to evaluate the entropy change along the pair of lines shown above. Then
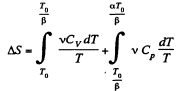
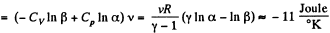
Q. 135. Vessels 1 and 2 contain v = 1.2 moles of gaseous helium. The ratio of the vessels' volumes V2/V1 = α = 2.0, and the ratio of the absolute temperatures of helium in them T1/T2 = β = 1.5. Assuming the gas to be ideal, find the difference of gas entropies in these vessels, S2 - S1.
Solution. 135. To calculate the required entropy difference we only have to calculate the entropy difference for a process in which the state of the gas in vessel 1 is changed to that in vessel 2.
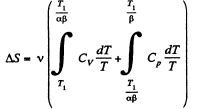
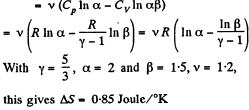
Q. 136. One mole of an ideal gas with the adiabatic exponent y goes through a polytropic process as a result of which the absolute temperature of the gas increases τ-fold. The polytropic constant equals n. Find the entropy increment of the gas in this process.
Solution. 136. For the polytropic process with index n
pVn = constant
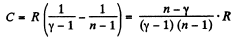
So 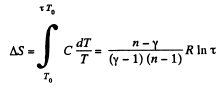
Q. 137. The expansion process of v = 2.0 moles of argon proceeds so that the gas pressure increases in direct proportion to its volume. Find the entropy increment of the gas in this process provided its volume increases α = 2.0 times.
Solution. 137. The process in question may be written as
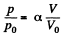
where a is a constant and p0, V0 are some reference values.
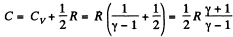
Along the line volume increases α times then so does the pressure. The temperature must then increase α2 times. Thus
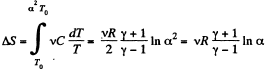
if 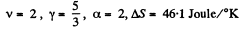
Q. 138. An ideal gas with the adiabatic exponent γ goes through a process p = p0 — αV, where p0 and α are positive constants, and V is the volume. At what volume will the gas entropy have the maximum value?
Solution. 138. Let (p1, V1) be a reference point on the line
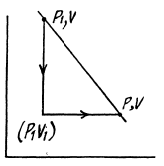
p = P0 - αV
and le t (p, V) be any other point.
The entropy difference
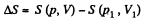
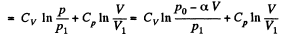
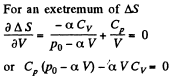
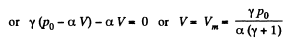
This gives a maximum of 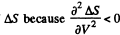
(Note : a maximum of ΔS is a maximum of S (p, V))
Q. 139. One mole of an ideal gas goes through a process in which the entropy of the gas changes with temperature T as S = aT + Cv In T, where a is a positive constant, Cv is the molar heat capacity of this gas at constant volume. Find the volume dependence of the gas temperature in this process if T = T0 at V = V0.
Solution. 139. Along the process line : S = aT + CyIn T
or the specific heat is : 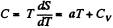
O n the other hand : : dQ = CdT = CvdT+pdV for an ideal gas.
Thus, 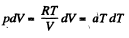
or 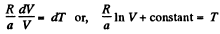
Using 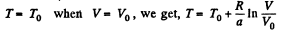
Q. 140. Find the entropy increment of one mole of a Van der Waals gas due to the isothermal variation of volume from V1 to V2. The Van der Waals corrections are assumed to be known.
Solution. 140. For a Vander Waal gas
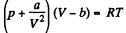
The entropy change along an isotherm can be calculated from

It follows from (Q.129) that
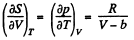
assuming a, b to be known constants.
Thus 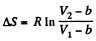
Q. 141. One mole of a Van der Waals gas which had initially the volume V1 and the temperature T1 was transferred to the state with the volume V2 and the temperature T2. Find the corresponding entropy increment of the gas, assuming its molar heat capacity Cv to be known.
Solution. 141.
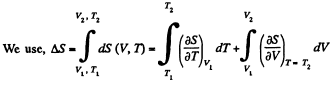
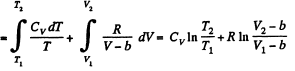
assuming Cv , a, b to be known constants.
Q. 142. At very low temperatures the heat capacity of crystals is equal to C = aT3, where a is a constant. Find the entropy of a crystal as a function of temperature in this temperature interval.
Solution. 142. We can take 5 → 0 as T → 0 Then
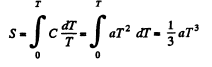
Q. 143. Find the entropy increment of an aluminum bar of mass m = 3.0 kg on its heating from the temperature T1 = 300 K up to T2 = 600 K if in this temperature interval the specific heat capacity of aluminum varies as c = a + bT, where a = 0.77 J/(g• K), b = 0.46 mJ/(g• K2).
Solution. 143.
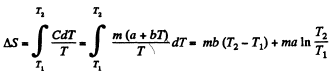
Q. 144. In some process the temperature of a substance depends on its entropy S as T = aSn, where a and n are constants. Find the corresponding heat capacity C of the substance as a function of S. At what condition is C < 0?
Solution. 144.
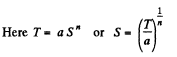
Then 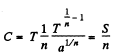
Clearly C < 0 if n < 0.
Q. 145. Find the temperature T as a function of the entropy S of a substance for a polytropic process in which the heat capacity of the substance equals C. The entropy of the substance is known to be equal to S0 at the temperature T0. Draw the approximate plots T (S) for C > 0 and C < 0.
Solution. 145.
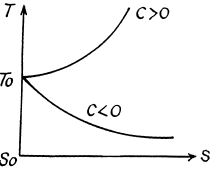
We know,
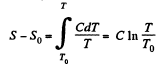
assuming C to be a known constant.
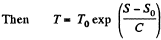
Q. 146. One mole of an ideal gas with heat capacity Cv goes through a process in which its entropy S depends on T as S = α/T, where a is a constant. The gas temperature varies from T1 to T2. Find:
(a) the molar heat capacity of the gas as a function of its temperature;
(b) the amount of heat transferred to the gas;
(c) the work performed by the gas.
Solution. 146. 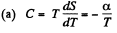
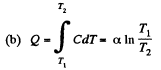
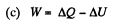
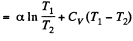
Since for an ideal gas Cv is constant and ΔU = CV(T2- T1)
Q. 147. A working substance goes through a cycle within which the absolute temperature varies n-fold, and the shape of the cycle is shown in (a) Fig. 2.4a; (b) Fig. 2.4b, where T is the absolute temperature, and S the entropy. Find the efficiency of each cycle.
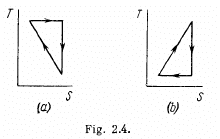
Solution. 147.
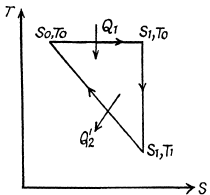
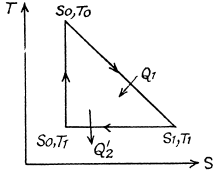
(a) We have from the definition
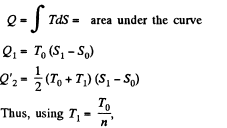
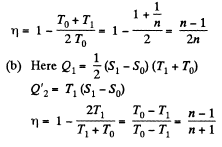
Q. 148. One of the two thermally insulated vessels interconnected by a tube with a valve contains v = 2.2 moles of an ideal gas. The other vessel is evacuated. The valve having been opened, the gas increased its volume n = 3.0 times. Find the entropy increment of the gas.
Solution. 148. In this case, called free expansion no work is done and no heat is exchanged. So internal eneigy must remain unchanged Uf = Ui For an ideal gas this implies constant temperature Tf = Ti. The process is irreversible but the entropy change can be calculated by considering a reversible isothermal process. Then, as before

Q. 149. A weightless piston divides a thermally insulated cylinder into two equal parts. One part contains one mole of an ideal gas with adiabatic exponent γ, the other is evacuated. The initial gas temperature is T0. The piston is released and the gas fills the whole volume of the cylinder. Then the piston is slowly displaced back to the initial position. Find the increment of the internal energy and the entropy of the gas resulting from these two processes.
Solution. 149. The process consists of two parts. The first part is free expansion in which Uf = Ui. The second part is adiabatic compression in which work done results in change of internal energy. Obviously,
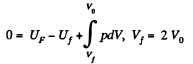
Now in the first part 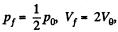 because there is no change of temperature.
because there is no change of temperature.
In the second part, 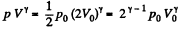
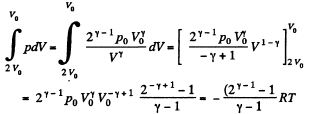
Thus 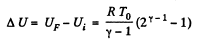
The entropy change 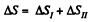
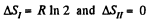 as the process is reversible adiabatic. Thus ΔS = R In 2.
as the process is reversible adiabatic. Thus ΔS = R In 2.
Q. 150. An ideal gas was expanded from the initial state to the volume V without any heat exchange with the surrounding bodies. Will the final gas pressure be the same in the case of (a) a fast and in the case of (b) a very slow expansion process?
Solution. 150. In all adiabatic processes
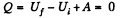
by virtue of the first law of thermodynamics. Thus,
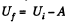
For a slow process, 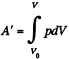 where for a quasistatic adiabatic process
where for a quasistatic adiabatic process 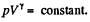
On the other hand for a fast process the external work done is 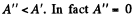 for free expansion.
for free expansion. 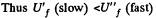
Since U depends on temperature only, 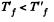
Consequently, 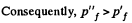
(From the ideal gas equation pV = RT)
Q. 151. A thermally insulated vessel is partitioned into two parts so that the volume of one part is n = 2.0 times greater than that of the other. The smaller part contains v1 = 0.30 mole of nitrogen, and the greater one v2 = 0.70 mole of oxygen. The temperature of the gases is the same. A hole is punctured in the partition and the gases are mixed. Find the corresponding increment of the system's entropy, assuming the gases to be ideal.
Solution. 151. 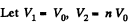
Since the temperature is the same, the required entropy change can be calculated by considering isothermal expansion of the gas in either parts into the whole vessel.
Thus 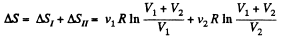
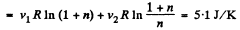
Q. 152. A piece of copper of mass m1 = 300 g with initial temperature t1 = 97°C is placed into a calorimeter in which the water of mass m2 = 100 g is at a temperature t2 = 7°C. Find the entropy increment of the system by the moment the temperatures equalize. The heat capacity of the calorimeter itself is negligibly small.
Solution. 152. Let c1 = specific heat of copper specific heat of water = c2
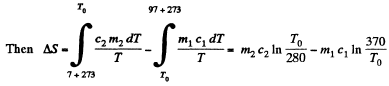
T0 is found from
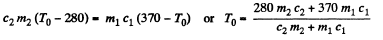
using 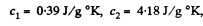
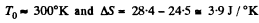
Q. 153. Two identical thermally insulated vessels interconnected by a tube with a valve contain one mole of the same ideal gas each. The gas temperature in one vessel is equal to T1 and in the other, T2. The molar heat capacity of the gas of constant volume equals Cv. The valve having been opened, the gas comes to a new equilibrium state. Find the entropy increment ΔS of the gas. Demonstrate that ΔS > 0.
Solution. 153. For an ideal gas the internal energy depends on temperature only. We can consider the process in question to be one of simultaneous free expansion. Then the total energy U = U1 + U2. Since
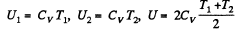
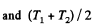 is the final temperature. The entropy change is obtained by considering isochoric processes because in effect, the gas remains confined to its vessel.
is the final temperature. The entropy change is obtained by considering isochoric processes because in effect, the gas remains confined to its vessel.
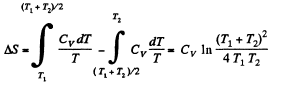
Since 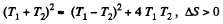
Q. 154. N atoms of gaseous helium are enclosed in a cubic vessel of volume 1.0 cm3 at room temperature. Find:
(a) the probability of atoms gathering in one half of the vessel;
(b) the approximate numerical value of N ensuring the occurrence of this event within the time interval 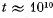 years (the age of the Universe).
years (the age of the Universe).
of this event within the time interval t 101° years (the age of the Universe).
Solution. 154. (a) Each atom has a probability 1/2 to be in either campartment Thus
p = 2-N
(b) Typical atomic velocity at room temperature is 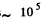 cm/s so it takes an atom 10-5 sec to cross the vessel. This is the relevant time scale for our problem. Let T = 10-5 sec, then in time t there will be t/ T crossing or arrangements of the atoms. Ttys will be large enough to produce the given arrangement if
cm/s so it takes an atom 10-5 sec to cross the vessel. This is the relevant time scale for our problem. Let T = 10-5 sec, then in time t there will be t/ T crossing or arrangements of the atoms. Ttys will be large enough to produce the given arrangement if
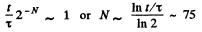
Q. 155. Find the statistical weight of the most probable distribution of N = 10 identical molecules over two halves of the cylinder's volume. Find also the probability of such a distribution.
Solution. 155. The statistical weight is
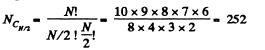
The probability distribution is
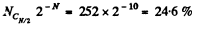
Q. 156. A vessel contains N molecules of an ideal gas. Dividing mentally the vessel into two halves A and B, find the probability that the half A contains n molecules. Consider the cases when N = 5 and n = 0, 1, 2, 3, 4, 5.
Solution. 156. The probabilites that the Jia lf A contains n molecules is
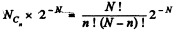
Q. 157. A vessel of volume V0 contains N molecules of an ideal gas. Find the probability of n molecules getting into a certain separated part of the vessel of volume V. Examine, in particular, the case V = V0/2.
Solution. 157. The probability of one molecule being confined to the marked volume is
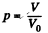
We can choose this molecule in many 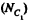 ways. The probability that n molecules get confined to the marked volume is cearly
ways. The probability that n molecules get confined to the marked volume is cearly
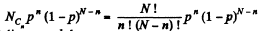
Q. 158. An ideal gas is under standard conditions. Find the diameter of the sphere within whose volume the relative fluctuation of the number of molecules is equal to η = 1.0.10-3. What is the average number of molecules inside such a sphere?
Solution. 158. In a sphere of diameter d there are

where n0 = Loschmidt’s number = No. of molecules per unit volume (1 cc) under NTP. The relative fluctuation in this number is
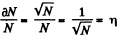
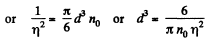
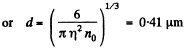
The average number of molecules in this sphere is 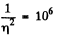
Q. 159. One mole of an ideal gas consisting of monatomic molecules is enclosed in a vessel at a temperature T0 = 300 K. How many times and in what way will the statistical weight of this system (gas) vary if it is heated isochorically by ΔT = 1.0 K?
Solution. 159. For a monoatomic gas 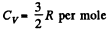
The entropy change in the process is
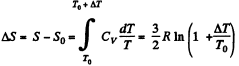
Now from the Boltzmann equation
S = k lnΩ

Thus the statistical weight increases by this factor.
FAQs on Irodov Solutions: The Second Law of Thermodynamics Entropy- 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the second law of thermodynamics? |  |
| 2. How is entropy related to the second law of thermodynamics? |  |
| 3. Can you explain the concept of entropy in thermodynamics? |  |
| 4. What are the practical implications of the second law of thermodynamics? |  |
| 5. How does the second law of thermodynamics relate to real-world applications? |  |

|
Explore Courses for JEE exam
|

|

















