Irodov Solutions: Interference of Light- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.86. The convex surface of a piano-convex glass lens comes into contact with a glass plate. The curvature radius of the lens's convex surface is R, the wavelength of light is equal to λ. Find the width Δr of a Newton ring as a function of its radius r in the region where Δr ≪ r.
Ans. We have
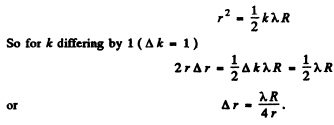
Q.87. The convex surface of a plano-convex glass lens with curvature radius R = 40 cm comes into contact with a glass plate. A certain ring observed in reflected light has a radius r = 2.5 mm. Watching the given ring, the lens was gradually removed from the plate by a distance Δh = 5.0 p,m. What has the radius of that ring become equal to?
Ans.
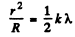
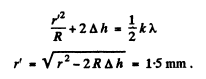
Q.88. At the crest of a spherical surface of a piano-convex lens there is a ground-off plane spot of radius r0 = 3.0 mm through which the lens comes into contact with a glass plate. The curvature radius of the lens's convex surface is equal to R = 150 cm. Find the radius of the sixth bright ring when observed in reflected light with wavelength λ = 655 nm.
Ans.
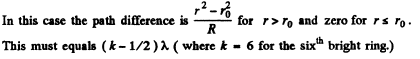
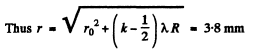
Q.89. A piano-convex glass lens with curvature radius of spherical surface R = 12.5 cm is pressed against a glass plate. The diameters of the tenth and fifteenth dark Newton's rings in reflected light are equal to d1 = 1.00 mm and d2 = 1.50 mm. Find the wavelength of light.
Ans.
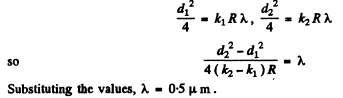
Q.90. Two piano-convex thin glass lenses are brought into contact with their spherical surfaces. Find the optical power of such a system if in reflected light with wavelength λ = 0.60 pm the diameter of the fifth bright ring is d = 1.50 mm.
Ans.
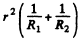
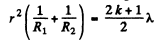
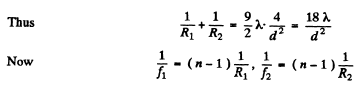
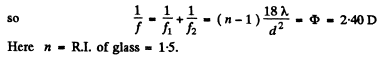
Q.91. Two thin symmetric glass lenses, one biconvex and the other biconcave, are brought into contact to make a system with optical power φ = 0.50 D. Newton's rings are observed in reflected light with wavelength λ = 0.61 μm. Determine:
(a) the radius of the tenth dark ring;
(b) how the radius of that ring will change when the space between the lenses is filled up with water.
Ans.
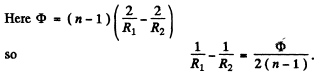
Q.92. The spherical surface of a piano-convex lens comes into contact with a glass plate. The space between the lens and the plate is filled up with carbon dioxide. The refractive indices of the lens, carbon dioxide, and the plate are equal to n1 = 1.50, n2 = 1.63, and n3 = 1.70 respectively. The curvature radius of the spherical surface of the lens is equal to R = 100 cm. Determine the radius of the fifth dark Newton's ring in reflected light with wavelength λ = 0.50 μm.
Ans.
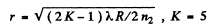
Q.93. In a two-beam interferometer the orange mercury line composed of two wavelengths λ1 = 576.97 nm and λ2 = 579.03 nm is employed. What is the least order of interference at which the sharpness of the fringe pattern is the worst?
Ans.
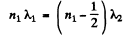
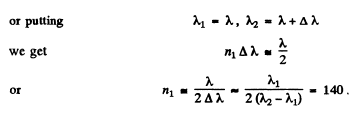
Q.94. In Michelson's interferometer the yellow sodium line composed of two wavelengths λ1 = 589.0 nm and λ2 = 589.6 nm was used. In the process of translational displacement of one of the mirrors the interference pattern vanished periodically (why?). Find the displacement of the mirror between two successive appearances of the sharpest pattern.
Ans.
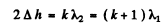
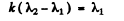
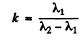
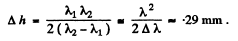
Q.95. When a Fabry-Perot &talon is illuminated by monochromatic light with wavelength λ an interference pattern, the system of con-
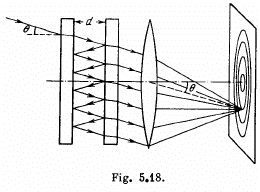
centric rings, appears in the focal plane of a lens (Fig. 5.18). The thickness of the &talon is equal to d. Determine how (a) the position of rings; (b) the angular width of fringes depends on the order of interference.
Ans.
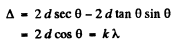
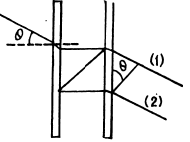
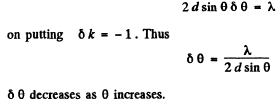
Q.96. For the Fabry-Perot etalon of thickness d = 2.5 cm find:
(a) the highest order of interference of light with wavelength λ = 0.50 p,m;
(b) the dispersion region Δλ , i.e. the spectral interval of wavelengths, within which there is still no overlap with other orders of interference if the observation is carried out approximately at wavelength λ = 0.50 pm.
Ans.
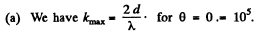
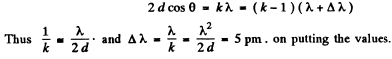
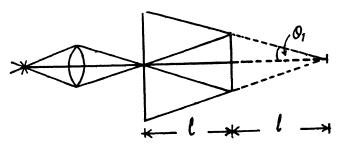
Q.83. Monochromatic light passes through an orifice in a screen Sc (Fig. 5.17) and being reflected from a thin transparent plate P produces fringes of equal inclination on the screen.
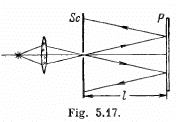
The thickness of the plate is equal to d, the distance between the plate and the screen is l, the radii of the ith and kth dark rings are ri and rk. Find the wavelength of light taking into account that 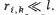
Ans. For small angles θ we write for dark fringes
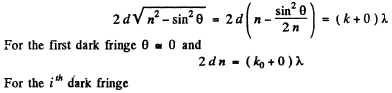
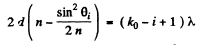
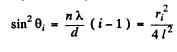
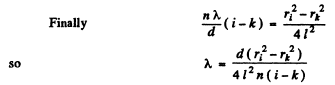
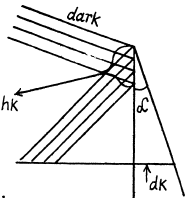
Q.84. A plane monochromatic light wave with wavelength λ falls on the surface of a glass wedge whose faces form an angle α ≪ 1. The plane of incidence is perpendicular to the edge, the angle of incidence is θ1. Find the distance between the neighbouring fringe maxima on the screen placed at right angles to reflected light.
Ans. We have the usual equation for maxima

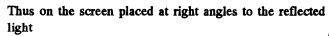
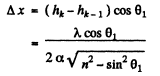
Q.85. Light with wavelength A. = 0.55 pm from a distant point source falls normally on the surface of a glass wedge. A fringe pattern whose neighbouring maxima on the surface of the wedge are separated by a distance Δx = 0.21 mm is observed in reflected light. Find:
(a) the angle between the wedge faces;
(b) the degree of light monochromatism (Δλ /λ ) if the fringes disappear at a distance 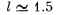 cm from the wedge's edge
cm from the wedge's edge
Ans.
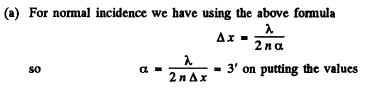
(b) In a distance / on the wedge there are 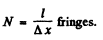
If the fringes disappear there, it must be due to the fact that the maxima due to the component of wavelength λ coincide with the mainima due to the component of
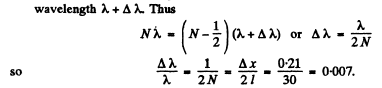
The answer given in the book is off by a factor 2.
FAQs on Irodov Solutions: Interference of Light- 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is interference of light? |  |
| 2. How does interference of light occur? |  |
| 3. What are the conditions required for interference of light to occur? |  |
| 4. What are the applications of interference of light? |  |
| 5. How can interference of light be explained using the wave theory of light? |  |
















