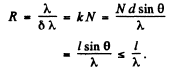Irodov Solutions: Diffraction of Light- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download

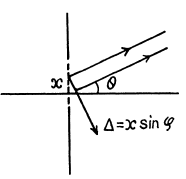
Q.119. Light with wavelength λ falls normally on a long rectangular slit of width b. Find the angular distribution of the intensity of light in the case of Fraunhofer diffraction, as well as the angular position of minima. 

Ans.  

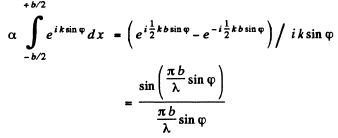
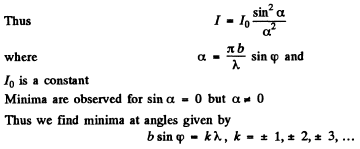
Q.120. Making use of the result obtained in the foregoing problem, find the conditions defining the angular position of maxima of the first, the second, and the third order. 

Ans.  

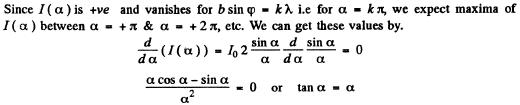
Solutions of this transcendental equation can be obtained graphically.
The first three solutions are

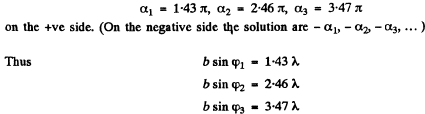
Asymptotically the solutions are

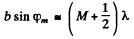
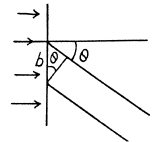
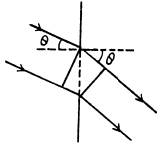
Q.121. Light with wavelength λ = 0.50 [tm falls on a slit of width b = 10 um at an angle θ₀ = 30° to its normal. Find the angular position of the first minima located on both sides of the central Fraunhofer maximum. 

Ans. The relation b sinθ = kλ for minima (when light is incident normally on the slit) has a simple interpretation 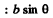  is the path difference between extreme wave normals emitted at angle θ

Q.122. A plane light wave with wavelength λ = 0.60 ti,m falls normally on the face of a glass wedge with refracting angle 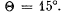 The opposite face of the wedge is opaque and has a slit of width b = 10 μm parallel to the edge. Find:
 (a) the angle Δθ between the direction to the Fraunhofer maximum of zeroth order and that of incident light;
 (b) the angular width of the Fraunhofer maximum of the zeroth order. 

Ans.

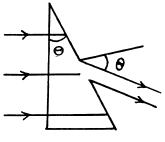
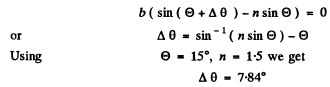
(b) The width of the central maximum is obtained from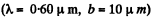  

Thus

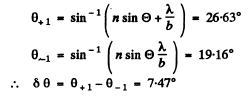
Q.123. A monochromatic beam falls on a reflection grating with period d = 1.0 mm at a glancing angle α₀ = 1.0°. When it is diffracted at a glancing angle α = 3.0° a Fraunhofer maximum of second order occurs. Find the wavelength of light. 

Ans.

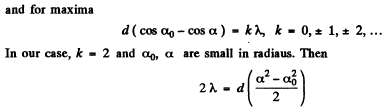
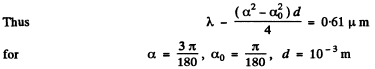
Q.124. Draw the approximate diffraction pattern originating in the case of the Fraunhofer diffraction from a grating consisting of three identical slits if the ratio of the grating period to the slit width is equal to (a) two; (b) three.

Ans. The general formula for diffraction from N slits is 

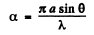
where

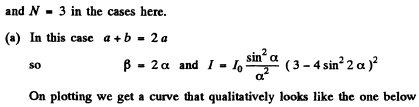
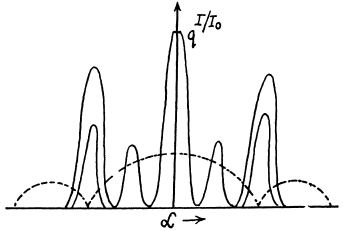
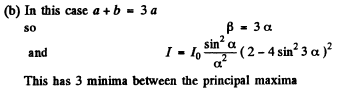
Q.125. With light falling normally on a diffraction grating, the angle of diffraction of second order is equal to 45° for a wavelength λ₁ = 0.65 μm. Find the angle of diffraction of third order for a wave length λ₂  =0 .50 1.1.m. 

Ans.

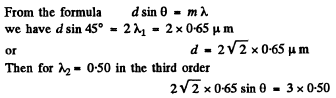
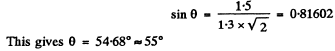
Q.126. Light with wavelength 535 nm falls normally on a diffraction grating. Find its period if the diffraction angle 35°corresponds to one of the Fraunhofer maxima and the highest order of spectrum is equal to five. 

Ans. The diffraction formula is

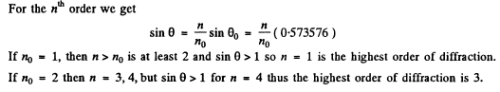
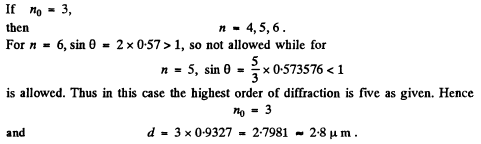
Q.127. Find the wavelength of monochromatic light falling normally on a diffraction grating with period d = 2.2 μm if the angle between the directions to the Fraunhofer maxima of the first and the second order is equal to Δθ = 15°. 

Ans. 

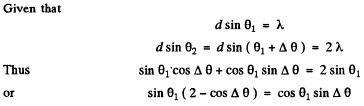
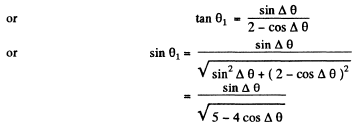
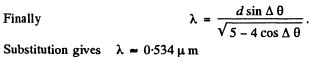
Q.128. Light with wavelength 530 nm falls on a transparent diffraction grating with period 1.50 lila. Find the angle, relative to the grating normal, at which the Fraunhofer maximum of highest order is observed provided the light falls on the grating (a) at right angles; (b) at the angle 60° to the normal. 

Ans. (a) Here the simple formula

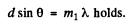
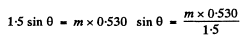
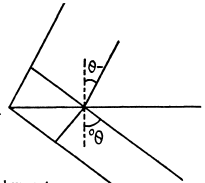
Q.129. Light with wavelength λ = 0.60 tim falls normally on a diffraction grating inscribed on a plane surface of a plano-convex cylindrical glass lens with curvature radius R = 20 cm. The period of the grating is equal to d = 6.0 μm. Find the distance between the principal maxima of first order located symmetrically in the focal plane of that lens. 

Ans. For the Lens

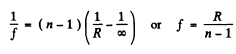
For the grating

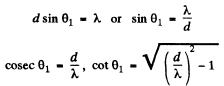
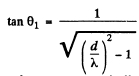
Hence the distance between the two symmetrically placed first order maxima 

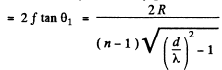
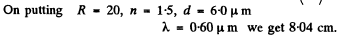
Q.130. A plane light wave with wavelength λ = 0.50 µm falls normally on the face of a glass wedge with an angle 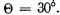 On the opposite face of the wedge a transparent diffraction grating with period d = 2.00 μm is inscribed, whose lines are parallel to the wedge's edge. Find the angles that the direction of incident light forms with the directions to the principal Fraunhofer maxima of the zero and the first order. What is the highest order of the spect rum? At what angle to the direction of incident light is it observed? 

Ans. The diffraction formula is easily obtained on taking account of the fact that the optical path in the glass wedge acquires a factor n (refractive index). We get

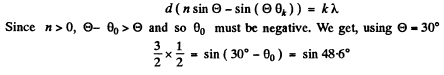
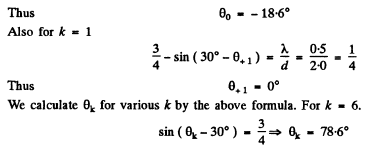
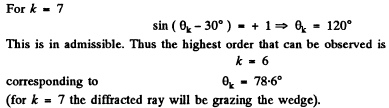
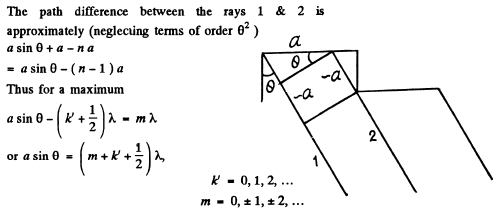
Q.131. A plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. 5.26. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. What is in this case the diffraction angle corresponding to the first maximum? 

Ans. The intensity of the central Fraunhofer maximum will be zero if the waves from successive grooves (not in the same plane) differ in phase by an odd multiple of n. Then since the phase difference is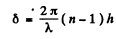

for the central ray we have

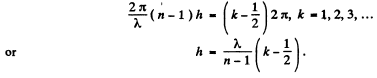
Q.132. Figure 5.27 illustrates an arrangement employed in observations of diffraction of light by ultrasound. A plane light wave with wavelength λ = 0.55 μm passes through the water-filled tank T in which a standing ultrasonic wave is sustained at a frequency v = 4.7 MHz. As a result of diffraction of light by the optically inhomogeneous periodic structure a diffraction spectrum can be observed in the focal plane of the objective O with focal length f = 35 cm. The separation between neighbouring maxima is Δx = 0.60 mm. Find the propagation velocity of ultrasonic oscillations in water. 

Ans. When standing ultra sonic waves are sustained in the tank it behaves like a grating whose grating element is 

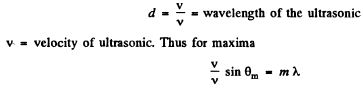
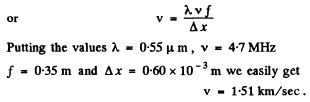
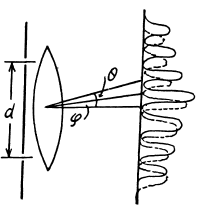
Q.133. To measure the angular distance ψ between the components of a double star by Michelson's method, in front of a telescope's lens a diaphragm was placed, which had two narrow parallel slits separated by an adjustable distance d. While diminishing d, the first smearing of the pattern was observed in the focal plane of the objective at d = 95 cm. Find ψ assuming the wavelength of light to be equal to λ = 0.55 μm. 

Ans.  Each star produces its own diffraction pattern in the focal plane o f the ob jective and these patterns are separated by angle As the distance d decreases the angle 0 between the neighbouring maxima in either diffraction pattern increases (sinθ - λ/d). When θ becomes equal to 2ψ the first deterioration o f v isib ility occurs because the maxima o f one system o f fringes coincide with the minima o f the other system. Thus from the condition

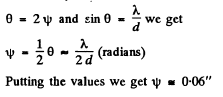
Q.134. A transparent diffraction grating has a period d = 1.50 μm. Find the angular dispersion D (in angular minutes per nanometres) corresponding to the maximum of highest order for a spectral line of wavelength λ = 530 nm of light falling on the grating (a) at right angles; (b) at the angle θ₀  = 45° to the normal. 

Ans.

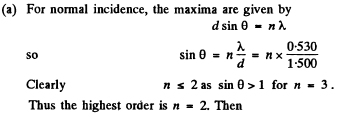
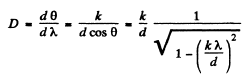
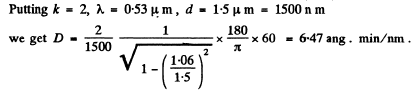
(b) We write the diffraction formula as

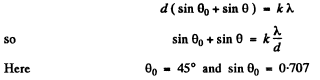
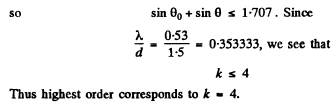
Q.135. Light with wavelength λ falls on a diffraction grating at right angles. Find the angular dispersion of the grating as a function of diffraction angle θ.

Ans.

Q.136. Light with wavelength λ = 589.0 nm falls normally on a diffraction grating with period d = 2.5 μm, comprising N = = 10 000 lines. Find the angular width of the diffraction maximum of second order.

Ans.

or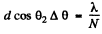

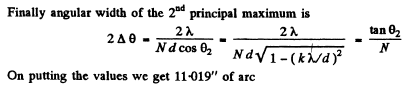
Q.137. Demonstrate that when light falls on a diffraction grating at right angles, the maximum resolving power of the grating cannot exceed the value l/λ where l is the width of the grating and λ is the wavelength of light. 

Ans.  Using