Irodov Solutions: Transport Phenomena- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download

Q. 220. Calculate what fraction of gas molecules
 (a) traverses without collisions the distances exceeding the mean free path λ;
 (b) has the free path values lying within the interval from λ to 2λ.

Solution. 220. (a) The fraction of gas molecules which traverses distances exceeding the mean free path without collision is just the probability to traverse the distance s = λ without collision.

Thus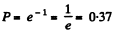 

(b) This probability is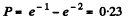   

Q. 221. A, narrow molecular beam makes its way into a vessel filled with gas under low pressure. Find the mean free path of molecules if the beam intensity decreases η-fold over the distance Δl. 

Solution. 221. From the formula 

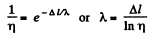
Q. 222. Let αdt be the probability of a gas molecule experiencing a collision during the time interval dt; α is a constant. Find:
 (a) the probability of a molecule experiencing no collisions during the time interval t; 
 (b) the mean time interval between successive collisions.

Solution. 222. (a) Let P (f) = probability of no collision in the interval (0, t). Then

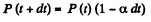
or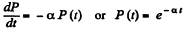  

where we have used P (0) = 1

(b) The mean interval between collision is also the mean interval of no collision. Then

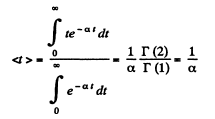
Q. 223. Find the mean free path and the mean time interval be- tween successive collisions of gaseous nitrogen molecules
 (a) under standard conditions;
 (b) at temperature t = 0°C and pressure p = 1.0 nPa (such a pressure can be reached by means of contemporary vacuum pumps). 

Solution. 223.

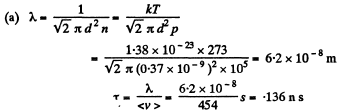
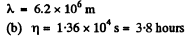
Q. 224. How many times does the mean free path of nitrogen molecules exceed the mean distance between the molecules under standard conditions? 

Solution. 224. The mean distance between molecules is of the order

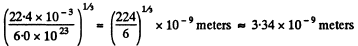
This is about 18.5 times smaller than the mean free path calculated in 2.223 (a) above.

Q. 225. Find the mean free path of gas molecules under standard conditions if the Van der Waals constant of this gas is equal to b = 40 ml/mol. 

Solution. 225. We know that the Vander Waal’s constant b is four times the molecular volume. Thus

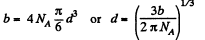
Hence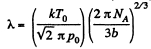 

Q. 226. An acoustic wave propagates through nitrogen under standard conditions. At what frequency will the wavelength be equal to the mean free path of the gas molecules?

Solution. 226. The volodty of sound in N₂ is

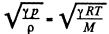
so,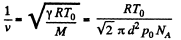 

or,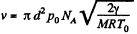  

Q. 227. Oxygen is enclosed at the temperature 0°C in a vessel with the characteristic dimension l = 10 mm (this is the linear dimension determining the character of a physical process in question). Find: 

(a) the gas pressure below which the mean free path of the molecules λ > 1;
 (b) the corresponding molecular concentration and the mean distance between the molecules. 

Solution. 227. 

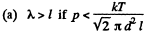
Now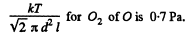  

(b) The corresponding n is obtained by dividing by kT and is 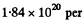  m³ = 1.84 uper c.c. and the corresponding mean distance is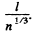

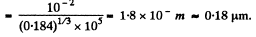
Q. 228. For the case of nitrogen under standard conditions find:
 (a) the mean number of collisions experienced by each molecule per second;
 (b) the total number of collisions occurring between the molecules within 1 cm³ of nitrogen per second.

Solution. 228. 

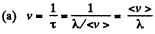
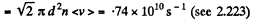
(b) Total number of collisions is

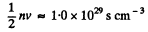
Note, the factor 1/2. When two molecules collide we must not count it twice.

Q. 229. How does the mean free path λ and the number of collisions of each molecule per unit time v depend on the absolute temperature of an ideal gas undergoing 

(a) an isochoric process;
 (b) an isobaric process?

Solution. 229. 

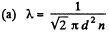
d is a constant and n is a constant for an isochoric process so X is constant for an isochoric process.

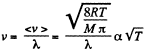
(b) 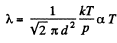 for an isobaric process.

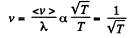 or an isobaric process.

Q. 230. As a result of some process the pressure of an ideal gas increases n-fold. How many times have the mean free path λ and the number of collisions 'of each molecule per unit time v changed and how, if the process is
 (a) isochoric;
 (b) isothermal?

Solution. 230. (a) In an isochoric process λ is constant and

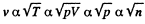
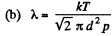 must decrease n times in an isothermal process and v must increase n times because <v > is constant in an isothermal process.

Q. 231. An ideal gas consisting of rigid diatomic molecules goes through an adiabatic process. How do the mean free path λ and the number of collisions of each molecule per second v depend in this process on
 (a) the volume V;
 (b) the pressure p;
 (c) the temperature T? 

Solution. 231. 

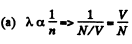
Thus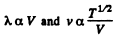 

But In an adiabatic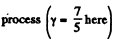 

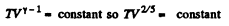
or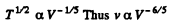  

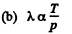
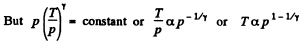
Thus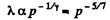    

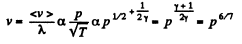
(c)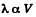 

But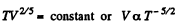   

Thus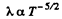 

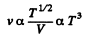
Q. 232. An ideal gas goes through a polytropic process with exponent n. Find the mean free path and the number of collisions of each molecule per second v as a function of
 (a) the volume V;
 (b) the pressure p;
 (c) the temperature T. 

Solution. 232. In the polytropic process of index n

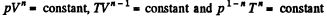
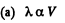
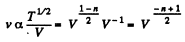
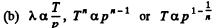
so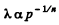  

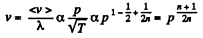
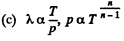
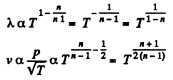
Q. 233. Determine the molar heat capacity of a polytropic process through which an ideal gas consisting of rigid diatomic molecules goes and in which the number of collisions between the molecules remains constant
 (a) in a unit volume;
 (b) in the total volume of the gas. 

Solution. 233. (a) The number of collisions between the jnolecules in a unit volume is

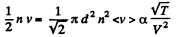
This remains constant in the poly process pV^-3 = constant

Using (Q.122) the molar specific heat for the polytropic process

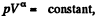
is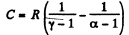 

Thus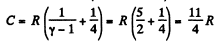 

It can also be written as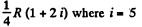 

(b) In this case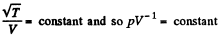 

so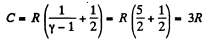  

It can also be written as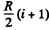 

Q. 234. An ideal gas of molar mass M is enclosed in a vessel of volume V whose thin walls are kept at a constant temperature T. At a moment t = 0 a small hole of area S is opened, and the gas starts escaping into vacuum. Find the gas concentration n as a function of time t if at the initial moment n (0) = n₀.

Solution. 234. We can assume that all molecules, incident on the hole, leak out. Then,

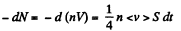
or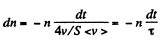  

Integrating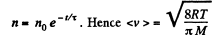 

Q. 235. A vessel filled with gas is divided into two equal parts 1 and 2 by a thin heat-insulating partition with two holes. One hole has a small diameter, and the other has a very large diameter (in comparison with the mean free path of molecules). In part 2 the gas is kept at a temperature η  times higher than that of part 1. How will the concentration of molecules in part 2 change and how many times after the large hole is closed? 

Solution. 235. If the temperature of the compartment 2 is η times more than that of compartment 1, it must contain 1/η times less number of molecules since pressure must be the same when the big hole is open. If M - mass of the gas in 1 than the mass of the gas in 2 must be M/η . So immediately after the big hole is closed.

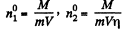
where m = mass of each molecule and 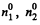  are concentrations in 1 and 2. A fter the big hole is closed the pressures will differ and concentration will become n₁ and n₂ where

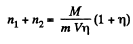
On the other hand

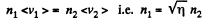
Thus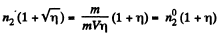  

So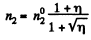 

Q. 236. As a result of a certain process the viscosity coefficient of an ideal gas increases α = 2.0 times and its diffusion coefficient β = 4.0 times. How does the gas pressure change and how many times? 

Solution. 236. We know

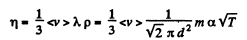
Thus η changing α times implies T changing α² times. On the other hand

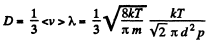
Thus D changing P times means 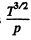 changing β times

So p must change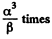 

Q. 237. How will a diffusion coefficient D and the viscosity coefficient η of an ideal gas change if its volume increases n times: (a) isothermally; (b) isobarically? 

Solution. 237.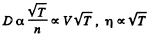 

(a) D will increase n times

η will remain constant if T is constant

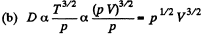
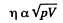
Thus D will increase 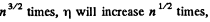   if p is constant

Q. 238. An ideal gas consists of rigid diatomic molecules. How will a diffusion coefficient D and viscosity coefficient η change and how many times if the gas volume is decreased adiabatically n =10 times? 

Solution. 238. 

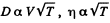
In an adiabatic process

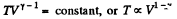
Now V is decreased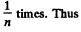 

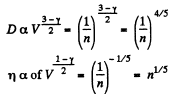
So D decreases n^4/5 times and η increase n^1/5 times.