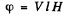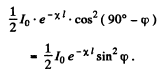Irodov Solutions: Dispersion and Absorption of Light- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download

Q.200. A free electron is located in the field of a monochromatic light wave. The intensity of light is I = 150 W/m², its frequency is ω = 3.4.10¹⁵  s^-1. Find:
 (a) the electron's oscillation amplitude and its velocity amplitude;
 (b) the ratio F_m/F_e, where F_m and F_e are the amplitudes of forces with which the magnetic and electric components of the light wave field act on the electron; demonstrate that that ratio is equal to 

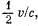
where v is the electron's velocity amplitude and c is the velocity of light. 

Instruction. The action of the magnetic field component can be disregarded in the equation of motion of the electron since the calculations show it to be negligible. 

Ans. In a travelling plane electromagnetic wave the intensity is simply the time averaged magnitude of the Poynting vector

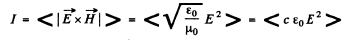
on using

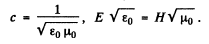
Now time averaged value of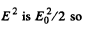  

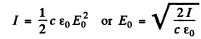
(a) Represent the electric field at any point by 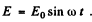 Then for the electron we have the equation.

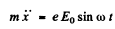
SO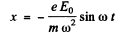  

he ampitude of the forced oscillation is

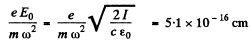
The velocity amplitude is clearly

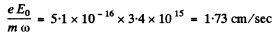
 (b) For the electric force F_e = amplitude of the electric force

- e E₀

For the magnetic force (which we have neglected above), it is

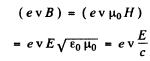
writing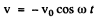 

where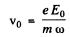  

we see that the magnetic force is apart from a sign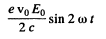 

Hence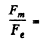 Ratio of amplitudes of the two forces

This is negligible and justifies the neglect of magnetic field of the electromagnetic wave in calculating v_o

Q.201. An electromagnetic wave of frequency ω propagates in dilute plasma. The free electron concentration in plasma is equal to n_o. Neglecting the interaction of the wave and plasma ions, find:
 (a) the frequency dependence of plasma permittivity;
 (b) how the phase velocity of the electromagnetic wave depends on its wavelength λ in plasma. 

Ans.  (a) It turns out that one can neglect the spatial dependence of the electric field as well as the magnetic field. Thus for a typical electron

The ions, will be practically unaffected. Then

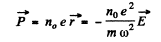
and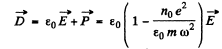

Hence the permittivity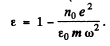

 (b) The phase velocity is given by

So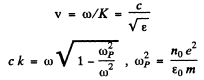               

Thus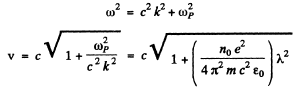   

Q.202. Find the free electron concentration in ionosphere if its refractive index is equal to n = 0.90 for radiowaves of frequency v = 100 MHz. 

Ans. From the previous problem

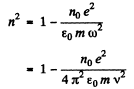
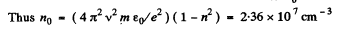
Q.203. Assuming electrons of substance to be free when subjected to hard X-rays, determine by what magnitude the refractive index of graphite differs from unity in the case of X-rays whose wavelength in vacuum is equal to λ = 50 pm. 

Ans. For hard x- rays, the electrons in graphite will behave as if nearly free and the formula of previous problem can be applied. Thus

and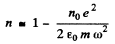   

on taking square root and neglecting higher order terms.

So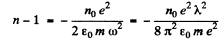   

We calculate n₀ as follows : There are 6 x 6 .023 x 10²³ electrons in 12 gms of graphite of density 1.6 gm/c.c. Thus

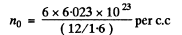
 Using the values of other constants and 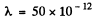  metre we get

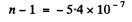
Q.204. An electron experiences a quasi-elastic force kx and a "fric- tion force" 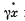 in the field of electromagnetic radiation. The E-component of the field varies as E = E₀ cos ωt. Neglecting the action of the magnetic component of the field, find:
 (a) the motion equation of the electron;
 (b) the mean power absorbed by the electron; the frequency at which that power is maximum and the expression for the maximum mean power. 

Ans. (a) The equation of the electron can (under the stated conditions) be written as

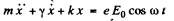
To solve this equation we shall find it convenient to use complex displacements. Consider the equation

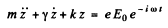
Its solution is

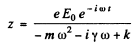
(we ignore transients.) 

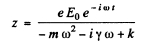
Writing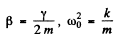  

we find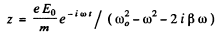  

Now x = Real part of z

where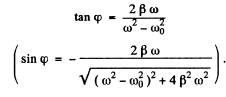

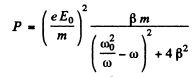
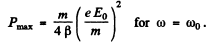
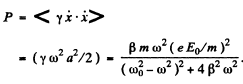
Q.205. In some cases permittivity of substance turns out to be a complex or a negative quantity, and refractive index, respectively, a complex (n' = n + ix) or an imaginary (n' = ix) quantity. Write the equation of a plane wave for both of these cases and find out the physical meaning of such refractive indices. 

Ans. Let us write the solutions of the wave equation in the form 

where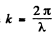 and λ. is the wavelength in the medium. If  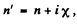then

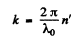
(λ₀ is the wavelength in vacuum) and the equation becomes

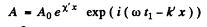
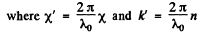
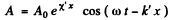
This represents a plane wave whose amplitude diminishes as it propagates to the right (provided X' < 0).

when 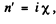 then similarly

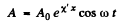
(on putting n = 0 in the above equation).
This represents a standing wave whose amplitude diminishes as one goes to the right (if X' < 0). The wavelength of the wave is infinite ( k' - 0 ).
Waves of the former type are realized inside metals as well as inside dielectrics when there is total reflection, (penetration of wave).

Q.5.206. A sounding of dilute plasma by radiowaves of various frequencies reveals that radiowaves with wavelengths exceeding λ_o = 0.75 m experience total internal reflection. Find the free electron concentration in that plasma. 

Ans.

Hence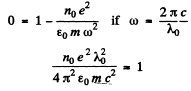

or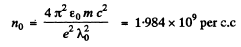 

Q.207. Using the definition of the group velocity u, derive Rayleigh's formula (5.5d). Demonstrate that in the vicinity of λ = λ' the velocity u is equal to the segment v' cut by the tangent of the curve v (λ) at the point λ' (Fig. 5.36). 

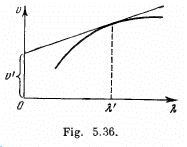
Ans. By definition

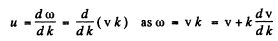
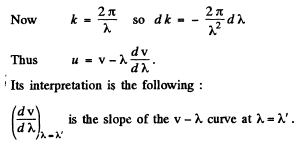
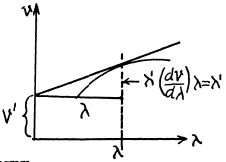
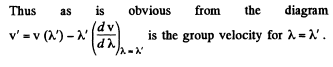
Q.208. Find the relation between the group velocity u and phase velocity v for the following dispersion laws: 

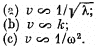
Here λ, k, and ω are the wavelength, wave number, and angular frequency. 

Ans.

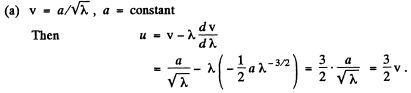
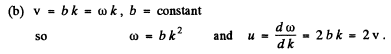
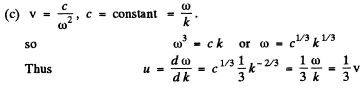
Q.209. In a certain medium the relationship between the group and phase velocities of an electromagnetic wave has the form uv = c², where c is the velocity of light in vacuum. Find the dependence of permittivity of that medium on wave frequency, εω. 

Ans. We have 

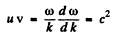
Integrating we find

so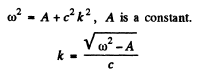

and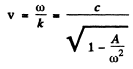

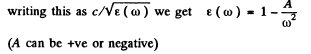
Q.210. The refractive index of carbon dioxide at the wavelengths 509, 534, and 589 nm is equal to 1.647,1.640, and 1.630 respectively. Calculate the phase and group velocities of light in the vicinity of λ = 534 nm. 

Ans. The phase velocity of light in the vicinity of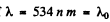  is obtained as

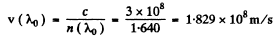
To get the group velocity we need to calculate

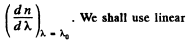
interpolation in the two intervals. Thus

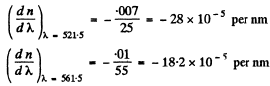
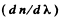
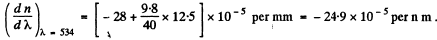
Q.211. A train of plane light waves propagates in the medium where the phase velocity v is a linear function of wavelength: v = a + bλ, where a and b are some positive constants. Demonstrate that in such a medium the shape of an arbitrary train of light waves is restored after the time interval ζ = 1/b. 

Ans. We write

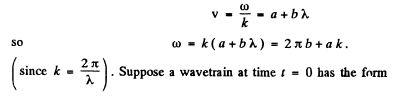
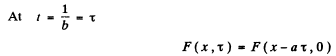
Q.212. A beam of natural light of intensity l₀ falls on a system of two crossed Nicol prisms between which a tube filled with certain solution is placed in a longitudinal magnetic field of strength H. The length of the tube is l, the coefficient of linear absorption of solution is x, and the Verdet constant is V. Find the intensity of light transmitted through that system. 

Ans. On passing through the first (polarizer) Nicol the intensity of light becomes 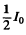  because one of the components has been cut off. On passing through the solution the plane of polarization of the light beam will rotate by