Irodov Solutions: Scattering of Particles: Rutherford-Bohr Atom | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.1. Employing Thomson's model, calculate the radius of a hydrogen atom and the wavelength of emitted light if the ionization energy of the atom is known to be equal to E = 13.6 eV.
Ans. The Thomson model consists of a uniformly charged nucleus in which the electrons are at rest at certain equilibrium points (the plum in the pudding model). For the hydrogen nucleus the charge on the nudeus is +e while the chaige on the electron is -e. The electron by symmetry must be at the centre of the nuclear charge where the potential (from problem (3.38a)) is
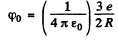
where R is the radius of the nucleur charge distribution. The potential energy of the electron is 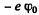 and since the electron is at rest, this is also the total eneigy. To ionize such an electron will require an energy of
and since the electron is at rest, this is also the total eneigy. To ionize such an electron will require an energy of 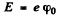
From this we find 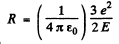
In Gaussian system the factor 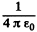 is missing.
is missing.
Putting the values we get R= 0.159 nm .
Light is emitted when the electron vibrates. If we displace the electron slightly inside the nucleus by giving it a push r in some radial direction and an eneigy δE of oscillation then since the potential at a distance r in the nucleus is
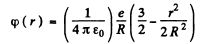
the total eneigy of the nucleus becomes
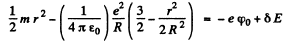
or 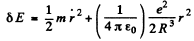
This is the eneigy of a harmonic oscillator whose frequency is 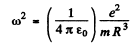
The vibrating electron emits radiation of frequency ω whose wavelength is
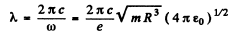
In Gaussian units the factor 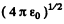 is missing.
is missing.
Putting the values we get 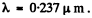
Q.2. An alpha particle with kinetic energy 0.27 MeV is deflected through an angle of 60° by a golden foil. Find the corresponding value of the aiming parameter.
Ans. Equation (6.1a) of the book reads in MKS units
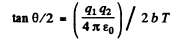
Thus 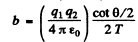
For α particle 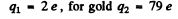
(In Gaussian units there is no factor 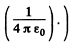
Substituting we get b = 0.731 pm .
Q.3. To what minimum distance will an alpha particle with kinetic energy T = 0.40 MeV approach in the case of a head-on collision to (a) a stationary Pb nucleus; (b) a stationary free Liz nucleus?
Ans. (a) In the Pb case we shall ignore the recoil of the nucleus both because Pb is quite heavy 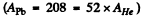 as well as because Pb in not free. Then for a head on collision, at the distance of closest approach, the K.E. of the α - particle must become zero (because α - particle will turn back at this point). Then
as well as because Pb in not free. Then for a head on collision, at the distance of closest approach, the K.E. of the α - particle must become zero (because α - particle will turn back at this point). Then
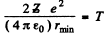
(No  in Gaussian units.). Thus putting the values
in Gaussian units.). Thus putting the values
rmin = 0.591 pm .
(b) Here we have to take account of the fact that part of the energy is spent in the recoil of Li nucleus. Suppose x1 coordinate of the α - particle from some arbitrary point on the line joining it to the Li nucleus, x2 = coordinate of the Li nucleus with respect to the same point Then we have the energy momentum equations
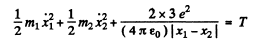
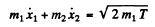
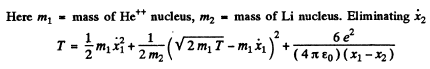
We complete the square on the right hand side and rewrite the above equation as
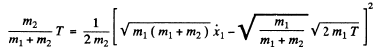
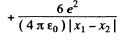
For the least distance of apporach, the second term on the right must be greatest which implies that the first term must vanish.
Thus 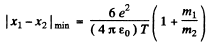
Using 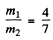 and other values we get
and other values we get
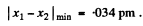
(In Gaussian units the factor 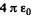 is absent).
is absent).
Q.4. An alpha particle with kinetic energy T = 0.50 MeV is deflected through an angle of θ = 90° by the Coulomb field of a stationary Hg nucleus. Find:
- All the formulas in this Part are given in the Gaussian system of units.
(a) the least curvature radius of its trajectory;
(b) the minimum approach distance between the particle and the nucleus.
Ans. We shall ignore the recoil of Hg nucleus.
(a) Let A be the point of closest approach to the centre 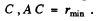 At A the motion is instantaneously circular because the radial velocity vanishes. Then if v0 is the speed of the particle at A, the following equations hold
At A the motion is instantaneously circular because the radial velocity vanishes. Then if v0 is the speed of the particle at A, the following equations hold
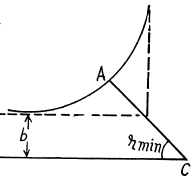
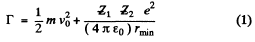
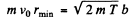 (2)
(2)
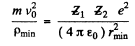 (3)
(3)
(This is Newton’s law. Here 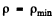 is the radius of curvature of the path at A and p is minimum at A by symmetry. ρ Finally we have Eqn. (6.1 a) in the form
is the radius of curvature of the path at A and p is minimum at A by symmetry. ρ Finally we have Eqn. (6.1 a) in the form
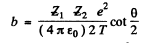 (4)
(4)
From (2) and (3) 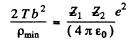
or 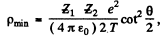
with 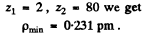
(b) From (2) and (4) we write
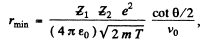
Substituting in (1)
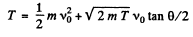
Solving for v0 we get 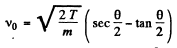
Then 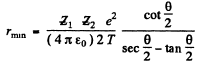
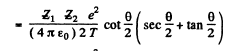
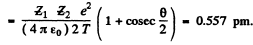
Q.5. A proton with kinetic energy T and aiming parameter b was deflected by the Coulomb field of a stationary Au nucleus. Find the momentum imparted to the given nucleus as a result of scattering.
Ans. By momentum conservation
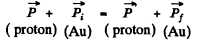
Thus the momentum transfered td the gold nucleus is clearly
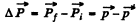
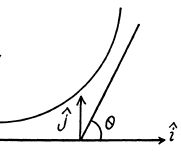
A lthough the momentum transfered to the Au nucleus is not small, the energy associated with this recoil is quite small and its effect back on the motion of the proton can be neglected to a first approximation. Then
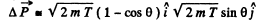
Here 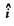 is the unit vector in the direction of the incident proton and
is the unit vector in the direction of the incident proton and 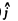 is normal to it on the side on which it is scattered. Thus
is normal to it on the side on which it is scattered. Thus
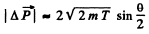
Or using tan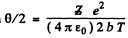 for the proton we get
for the proton we get
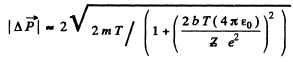
Q.6. A proton with kinetic energy T = 10 MeV flies past a stationary free electron at a distance b = 10 pm. Find the energy acquired by the electron, assuming the proton's trajectory to be rectilinear and the electron to be practically motionless as the proton flies by.
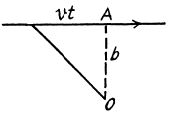
Ans. The proton moving by the electron first accelerates and then decele rates and it not easy to calculate the energy lost by the proton so energy conservation does not do the trick. Rather we must directly calculate the momentum acquire by the electron. By symmetry that momentum is along 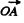 and its magnitude is
and its magnitude is
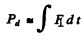
where 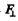 is the component along OA of the force on electron. Thus
is the component along OA of the force on electron. Thus
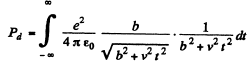
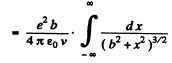
Evaluate the integral by substituting
x - 5 tan 8
Then 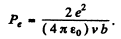
Then 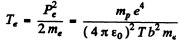
In Gaussian units there is no factor 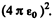 . Substituting the values we get
. Substituting the values we get
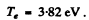
Q.7. A particle with kinetic energy T is deflected by a spherical potential well of radius R and depth Uo, i.e. by the field in which the potential energy of the particle takes the form
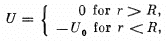
where r is the distance from the centre of the well. Find the relationship between the aiming parameter b of the particle and the angle 0 through which it deflects from the initial motion direction.
Ans. See the diagram on the next page. In the region where potential is nonzero, the kinetic eneigy of the particle is, by eneigy conservation, ____________ T + U0 and the mom entum of the particle has the m agnitude 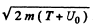 . . On the boundary the force is radial, so the tangential component of the momentum does not change :
. . On the boundary the force is radial, so the tangential component of the momentum does not change :
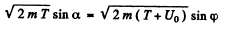
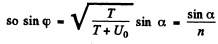
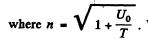 We also have
We also have
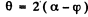
Therefore
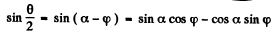
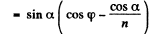
or 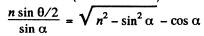
or 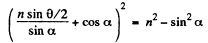
or 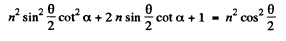
or 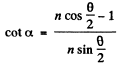
Hence 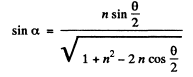
Finally, the impact parameter is
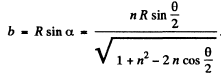
Q.8. A stationary ball of radius R is irradiated by a parallel stream of particles whose radius is r. Assuming the collision of a particle and the ball to be elastic, find:
(a) the deflection angle θ of a particle as a function of its aiming parameter b;
(b) the fraction of particles which after a collision with the ball are scattered into the angular interval between θ and θ + dθ;
(c) the probability of a particle to be deflected, after a collision with the ball, into the front hemispher
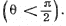
Ans. It is implied that the ball is too heavy to recoil.
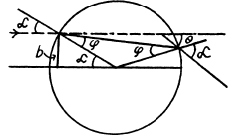
(a) The trajectory of the particle is symmetrical about the radius vector through the point of impact. It is clear from the diagram that
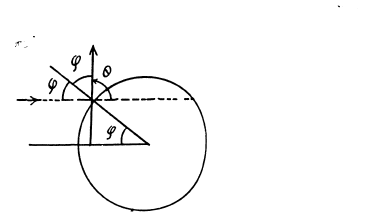
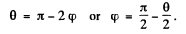
A lso 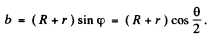
(b) With b defined above, the fraction of particles scattered between θ and θ + dθ (or the probability of the same) is
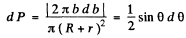
(c) This is
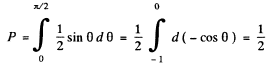
Q.9. A narrow beam of alpha particles with kinetic energy 1.0 MeV falls normally on a platinum foil 1.0 µm thick. The scattered particles are observed at an angle of 60° to the incident beam direction by means of a counter with a circular inlet area 1.0 cm2 located at the distance 10 cm from the scattering section of the foil. What fraction of scattered alpha particles reaches the counter inlet?
Ans. From the formula (6.1 b) of the book
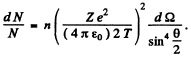
We have put 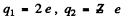 here. Also n = no. of Pt nuclei in the foil per unit area
here. Also n = no. of Pt nuclei in the foil per unit area
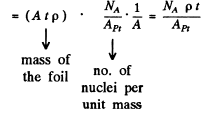
Using the values 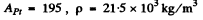
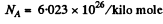
we get 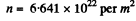
Also 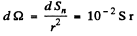
Substituting we get 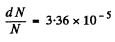
Q.10. A narrow beam of alpha particles with kinetic energy T = = 0.50 MeV and intensity I = 5.0.105 particles per second falls normally on a golden foil. Find the thickness of the foil if at a distance r = 15 cm from a scattering section of that foil the flux density of scattered particles at the angle θ = 60° to the incident beam is equal to J = 40 particles/(cm2•s).
Ans. a scattered flux density of J (perticles per unit area per second) equals 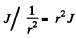 particles scattered per unit time per steradian in the given direction. Let n = concentration of the gold nuclei in the foil. Then
particles scattered per unit time per steradian in the given direction. Let n = concentration of the gold nuclei in the foil. Then
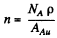
and the number of Au nuclei per unit area of the foil is nd where d = thickness of the foil Then from Eqn. (6.1 b) (note that n → nd here)
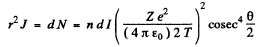
Here I is the number of α - particles falling on the foil per second
Hence 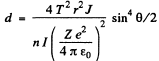
using Z = 79 , AAu = 197, ρ = 19-3 x 103 kg/m3 NA = 6.023 x 1026 / kilo mole and other data from the problem we get
d = 1.47 pm
Q.11. A narrow beam of alpha particles falls normally on a silver foil behind which a counter is set to register the scattered particles. On substitution of platinum foil of the same mass thickness for the silver foil, the number of alpha particles registered per unit time increased η = 1.52 times. Find the atomic number of platinum, assuming the atomic number of silver and the atomic masses of both platinum and silver to be known.
Ans. From the formula (6.1 b) of the book, wc find
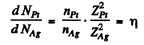
But since the foils have the same mass thickness ( = pd ) , we have
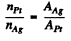
see the problem (6.9). Hence
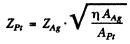
Substituting 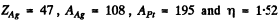 we get
we get
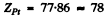
Q.12. A narrow beam of alpha particles with kinetic energy T = = 0.50 MeV falls normally on a golden foil whose mass thickness is pd = 1.5 mg/cm2. The beam intensity is I0 = 5.0.105 particles per second. Find the number of alpha particles scattered by the foil during a time interval ζ = 30 min into the angular interval:
(a) 59-61°;
(b) over θ0 = 60°.
Ans. (a) From Eqn. (6.1 b) we get
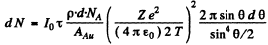
(we have used 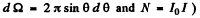
From the data
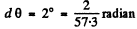
Also ZAu = 79 , AAm = 197 . Putting the values we get
dN = 1.63 x 106
(b) This number is
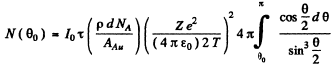
The integral is
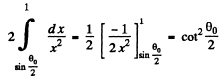
Thus
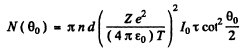
where n is the concentration of nuclei in the foil.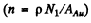
Substitution gives
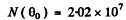
Q.13. A narrow beam of protons with velocity v = 6.106 m/s falls normally on a silver foil of thickness d = 1.0 p,m. Find the probability of the protons to be scattered into the rear hemisphere (θ > 90°).
Ans. The requisite probability can be written easily by analogy with (b) of the previous problem. It is
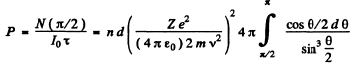
The integral is unity. Thus
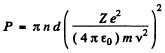
Substitution gives using
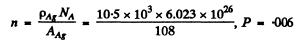
Q.14. A narrow beam of alpha particles with kinetic energy T = = 600 keV falls normally on a golden foil incorporating n = 1.1.1019 nuclei/cm2. Find the fraction of alpha particles scattered through the angles θ < θ0 = 20°.
Ans. Because of the 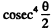 dependence of the scattering, the number of particles (or fraction) scattered through θ < θO cannot be calculated directly. But we can write this fraction as
dependence of the scattering, the number of particles (or fraction) scattered through θ < θO cannot be calculated directly. But we can write this fraction as
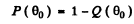
where Q (θO) is the fraction of particles scattered through 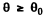 . This fraction has been calculated before and is (see the results of 6.12 (b))
. This fraction has been calculated before and is (see the results of 6.12 (b))
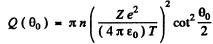
where n here is number of nuclei/cm2 . Using the data we get
Q = 0.4
Thus 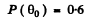
Q.15. A narrow beam of protons with kinetic energy T = 1.4 MeV falls normally on a brass foil whose mass thickness pd = 1.5 mg/cm2. The weight ratio of copper and zinc in the foil is equal to 7 : 3 respectively. Find the fraction of the protons scattered through the angles exceeding θ0 = 30°.
Ans. The relevant fraction can be immediately written down (see 6.12 (b)) (Note that the projectiles are protons)
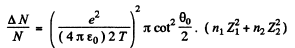
Here n1 (n2) is the number of Zn(Cu) nuclei per cm2 of the foil and Z1(Z2) is the atomic number of Zn(Cu). Now
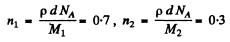
Here M i , M 2 are the mass numbers o f Zn and Cu.
Then, substituting the values Z1 = 30, Z2 = 29, M1 = 65.4, M2 = 63.5, we get
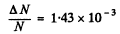
Q.16. Find the effective cross section of a uranium nucleus corresponding to the scattering of alpha particles with kinetic energy T = 1.5 MeV through the angles exceeding θ0 = 60°.
Ans. From the Rutherford scattering formula
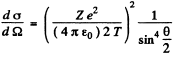
or 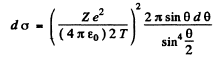
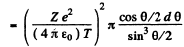
Then integrating from 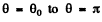 we get the required cross section
we get the required cross section
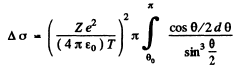
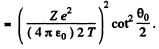
For U nucleus Z - 92 and we get on putting the values
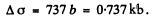
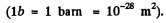
Q.17. The effective cross section of a gold nucleus corresponding to the scattering of monoenergetic alpha particles within the angular interval from 90° to 180° is equal to Δσ = 0.50 kb. Find:
(a) the energy of alpha particles;
(b) the differential cross section of scattering dσ/dΩ (kb/sr) corresponding to the angle θ = 60°.
Ans. (a) From the previous formula
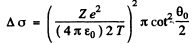
or 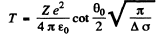
Substituting the values with Z = 79 we get (θO = 90°)
T = 0.903 MeV
(b) The differential scattering cross section is
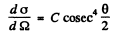
where 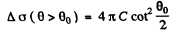
Thus from the given data
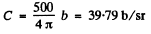
So
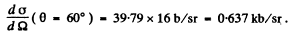
Q.18. In accordance with classical electrodynamics an electron moving with acceleration ω loses its energy due to radiation as
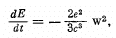
where e is the electron charge, c is the velocity of light. Estimate the time during which the energy of an electron performing almost harmonic oscillations with frequency ω = 5.1015 s-1 will decrease η = 10 times.
Ans. The formula in MKS units is
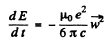
For an electron performing (linear) harmonic vibrations 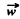 is in some definite directions with
is in some definite directions with
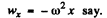
Thus
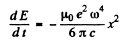
If the radiation loss is small (i.e. if ω is not too large), then the motion of the electron is always close to simple harmonic with slowly decreasing amplitude. Then we can write
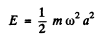
and 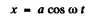
and average the above equation ignoring the variation of a in any cycle. Thus we get the equation, on using
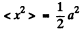
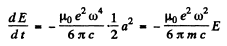
since 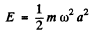 for a harmonic oscillator.
for a harmonic oscillator.
This equation integrates to
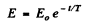
where 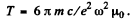
It is then seen that energy decreases η times in
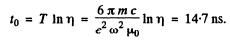
Q.19. Making use of the formula of the foregoing problem, estimate the time during which an electron moving in a hydrogen atom along a circular orbit of radius r = 50 pm would have fallen onto the nucleus. For the sake of simplicity assume the vector ω to be permanently directed toward the centre of the atom.
Ans. Moving around the nucleus, the electron radiates and its energy decreases. This means that the electron gets nearer the nucleus. By the statement of the problem we can assume that the electron is always moving in a circular orbit and the radial acceleration by Newton’s law is
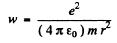
directed inwards. Thus
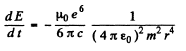
On the other hand in a circular orbit
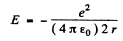
so
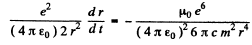
or
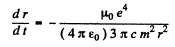
Integrating
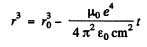
and the radius fells to zero in
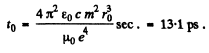
Q.20. Demonstrate that the frequency ω of a photon emerging when an electron jumps between neighbouring circular orbits of a hydrogen-like ion satisfies the inequality ωn > ω > ωn +1, where ωn and ωn +1 are the frequencies of revolution of that electron around the nucleus along the circular orbits. Make sure that as n → 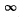 the frequency of the photon ω → ωn.
the frequency of the photon ω → ωn.
Ans. In a circular orbit we have the following formula
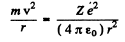
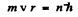
Then 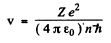
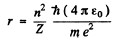
The energy E is 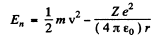
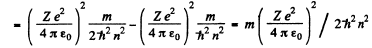
and the circular frequency of this orbit is
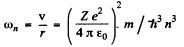
On the other hand the frequency co of the light emitted when the electron makes a transition n + 1 → n is
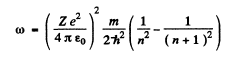
Thus the inequality
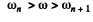
will result if
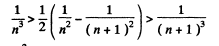
Or multiplying by n2(n + 1)2 we have to prove
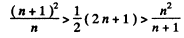
This can be written as
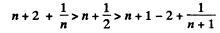
This is obvious because 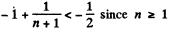
For laige n
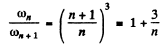
so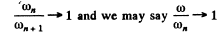
Q.21. A particle of mass m moves along a circular orbit in a centrosymmetrical potential field U (r) = kr212. Using the Bohr quantization condition, find the permissible orbital radii and energy levels of that particle.
Ans. We have the following equation (we ignore reduced mass effects)
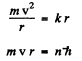
so 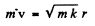
and 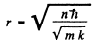
and 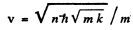
The energy levels are 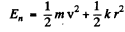
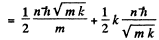
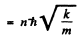
Q.22. Calculate for a hydrogen atom and a He + ion:
(a) the radius of the first Bohr orbit and the velocity of an electron moving along it;
(b) the kinetic energy and the binding energy of an electron in the ground state;
(c) the ionization potential, the first excitation potential and the wavelength of the resonance line (n' = 2 → n = 1).
Ans. The basic equations have been derived in the problem (6.20). We rewrite them here and determine the the required values.
(a) 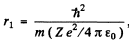 Thus Z = 1 for H , Z = 2 for He+
Thus Z = 1 for H , Z = 2 for He+
Thus r1 = 52.8 pm, for H atom
r2 = 26-.4 pm, for He+ ion
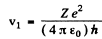
v1 = 2.191 x 106 m/s for H atom
= 4.382 x 106 m/s for He+ ion
(b) 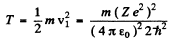
T = 13.65 eV for H atom T = 54.6 eV for He+ ion
In both cases E h = T because Eb = - E and E = - T (Recall that for coulomb force V = - 2 T )
(c) The ionization potential φi is given by
eφi = Eb
so φi = 13.65 volts for H atom
φi = 54.6 volts for He+ ion 13.65
The energy levels are
The energy levels are 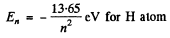 for H atom
for H atom
and 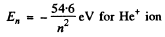
Thus 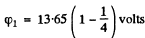 = 10.23 volts for H atom
= 10.23 volts for H atom
(φ1 = 4 x 10.23 = 40.9 volts for He+ ion
The wavelength of the resonance line
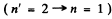 is given by
is given by
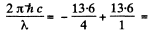 10.23 eV for H atom
10.23 eV for H atom
so λ = 121.2 nm for H atom
For He+ ion 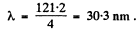
Q.23. Calculate the angular frequency of an electron occupying the second Bohr orbit of He+ ion.
Ans. This has been calculated before in problem (6.20). It is
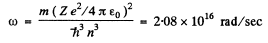
Q.24. For hydrogen-like systems find the magnetic moment tt n corresponding to the motion of an electron along the n-th orbit and the ratio of the magnetic and mechanical moments µn /Mn. Calculate the magnetic moment of an electron occupying the first Bohr orbit.
Ans. An electron moving in a circle with a time period T constitutes a current
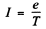
and forms a current loop of area πr2. This is equivalent to magnetic moment,
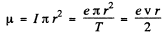
on using v = 2πr/T. Thus
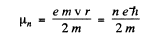
for the nth orbit. (In Gaussian units
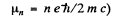
We see that
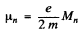
where 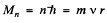 is the angular momentum
is the angular momentum
Thus 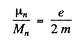
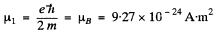
(In CGS units 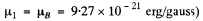
Q.25. Calculate the magnetic field induction at the centre of a hydrogen atom caused by an electron moving along the first Bohr orbit.
Ans. The revolving electron is equivalent to a circular current
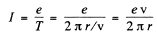
The magnetic induction
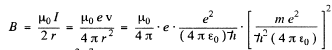
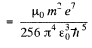
Substitution gives B = 12.56 T at the centre. (In Gaussian units
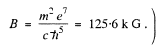
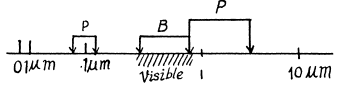
Q.26. Calculate and draw on the wavelength scale the spectral intervals in which the Lyman, Balmer, and Paschen series for atomic hydrogen are confined. Show the visible portion of the spectrum.
Ans. From the general formula for the transition n2 → n1
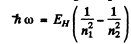
where EH ≥ 13.65eV. Then
(1) Lyman, n1 = 1, n2 = 2,3. Thus
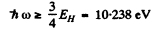
This conesponds to 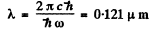
and Lyman lines have λ ≤ 0.121μm with the series limit at .0909μm
(2) Balmer : n2 = 2 , n3 = 3, 4 ,
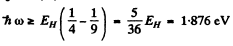
This corresponds to
λ = 0.65 μm
and Balmer series has λ ≤ 0.65μm with the series limit at X = 0.363μm
(3) Paschen : n2 = 3 , n1 = 4, 5,...
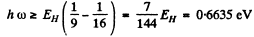
This corresponds to λ = 1.869μm
with the series limit at λ = 0.818μm
Q.27. To what series does the spectral line of atomic hydrogen belong if its wave number is equal to the difference between the wave numbers of the following two lines of the Balmer series: 486.1 and 410.2 nm? What is the wavelength of that line?
Ans. The Balmer line of wavelength 486-1 nm is due to the transition 4 → 2 while the Balmer line of wavelingth 4→2 nm is due to the transition 6→2. The line whose wave number corresponds to the difference in wave numbers of these two lines is due to the transition 6 → 4. That line belongs to the Brackett series. The wavelength of this line is
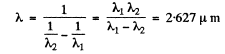
Q.28. For the case of atomic hydrogen find:
(a) the wavelengths of the first three lines of the Balmer series;
(b) the minimum resolving power λ/δλ of a spectral instrument capable of resolving the first 20 lines of the Balmer series.
Ans. The energies are
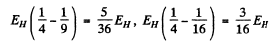
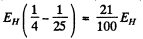
They correspond to wavelengths 654.2 n m , 484.6 n m and 433 nm
The nth line of the Balmer series has the energy
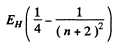
For n = 19, we get the wavelength 366.7450 nm
For n = 20 we get the wavelength 366.4470 nm
To resolve these lines we require a resolving power of
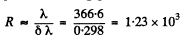
Q.29. Radiation of atomic hydrogen falls normally on a diffraction grating of width l = 6.6 mm. The 50th line of the Balmer series in the observed spectrum is close to resolution at a diffraction angle θ (in accordance with Rayleigh's criterion). Find that angle.
Ans. For the Balmer series
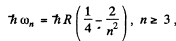
where 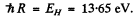 Thus
Thus
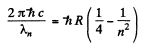
or 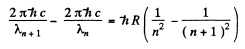
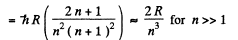
Thus 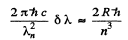
or 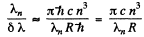
On the other hand for just resolution in a diffraction grating
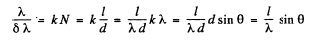
Hence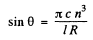
Substitution gives θ = 59.4°.
Q.30. What element has a hydrogen-like spectrum whose lines have wavelengths four times shorter than those of atomic hydrogen?
Ans. If all wavelengths are four times shorter but otherwise similar to the hydrogen atom spectrum then the energy levels of the given atom must be four times greater.
This means 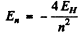
compared to 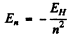 for hydrogen atom. Therefore the spectrum is that o f He+ ion (Z = 2).
for hydrogen atom. Therefore the spectrum is that o f He+ ion (Z = 2).
Q.31. How many spectral lines are emitted by atomic hydrogen excited to the n-th energy level?
Ans. Because of cascading all possible transitions are seen. Thus we look for the number of ways in which we can select upper and lower levels. The number of ways we can do this is
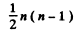
where the factor 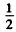 takes account of the fact that the photon emission always arises from upper lower transition.
takes account of the fact that the photon emission always arises from upper lower transition.
Q.32. What lines of atomic hydrogen absorption spectrum fall within the wavelength range from 94.5 to 130.0 nm?
Ans. These are the Lyman lines
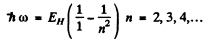
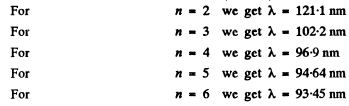
Thus at the level of accuracy of our calculation, there are four lines 121.1nm , 102.2nm , 96.9nm and 94.64nm .
Q.33. Find the quantum number n corresponding to the excited state of He+ ion if on transition to the ground state that ion emits two photons in succession with wavelengths 108.5 and 30.4 nm.
Ans. If the wavelengths are λ1,λ2 then the total energy of the excited start must be
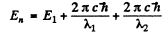
But 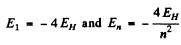 where we are ignoring reduced mass effects.
where we are ignoring reduced mass effects.
Then 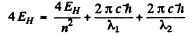
Substituting the values we get n2 = 23
which we take to mean n = 5. (The result is sensitive to the values of the various quantities and small differences get multiplied because difference of two large quantities is involved :
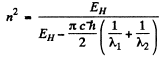
Q.34. Calculate the Rydberg constant R if He+ ions are known to have the wavelength difference between the first (of the longest wavelength) lines of the Balmer and Lyman series equal to Δλ = = 133.7 nm.
Ans. For the longest wavelength (first) line of the Balmer series we have on using the generalized Balmer formula
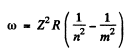
the result 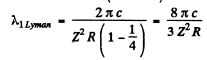
Then 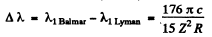
so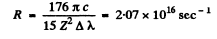
Q.35. What hydrogen-like ion has the wavelength difference between the first lines of the Balmer and Lyman series equal to 59.3 nm?
Ans. From the formula of the previous problem
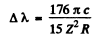
or 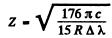
Substitution of Δλ = 59.3nm and and the previous problem gives Z = 3 This identifies the ion as Li++
Q.36. Find the wavelength of the first line of the He ion spectral series whose interval between the extreme lines is Δω = = 5.18.1015 s-1,
Ans. We start from the generalized Balmer formula
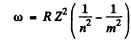
Here m = n + 1,n + 2, ....
The interval between extreme lines of this series (series n) is
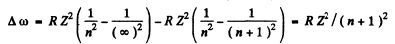
Hence
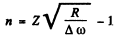
Then the angular frequency of the first line of this series (series n) is
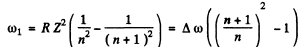
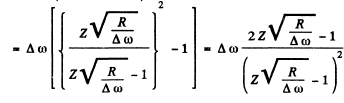
Then the wavelength will be
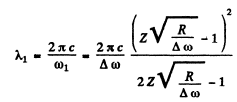
Substitution (with the value of R from problem 6.34 which is also the correct value determined directly) gives
λ1 = 0.468μm .
Q.37. Find the binding energy of an electron in the ground state of hydrogen-like ions in whose spectrum the third line of the Balmer series is equal to 108.5 nm.
Ans. For the third line of of Balmer series
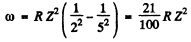
Hence 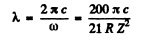
or 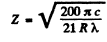
Substitution gives Z = 2. Hence the binding energy of the electron in the ground state of this ion is
Eb = 4EH = 4 x 13.65 = 54.6 eV
The ion is He+
Q.38. The binding energy of an electron in the ground state of He+ atom is equal to E0 = 24.6 eV. Find the energy required to remove both electrons from the atom.
Ans. To remove one electron requires 24.6 eV.
The ion that is left is He+ which in its ground start has a binding energy of 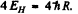
The complete binding energy of both electrons is then
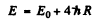
Substitution gives E = 79.1 eV
Q.39. Find the velocity of photoelectrons liberated by electromagnetic radiation of wavelength λ = 18.0 nm from stationary He ions in the ground state.
Ans. By conservation of energy
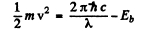
where 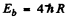 is the binding energy of the electron in the ground state of He+. (Recoil of He++ nucleus is neglected). Then
is the binding energy of the electron in the ground state of He+. (Recoil of He++ nucleus is neglected). Then
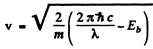
Substitution gives
v = 2.25 x 106 m/s
Q.40. At what minimum kinetic energy must a hydrogen atom move for its inelastic head-on collision with another, stationary, hydrogen atom to make one of them capable of emitting a photon? Both atoms are supposed to be in the ground state prior to the collision.
Ans. Photon can be emitted in H - H collision only if one o f the H is excited to an n = 2 state which then dexcites to n = 1 state by emitting a photon. Let v1 and v2 be the velocities of the two Hydrogen atoms after the collision and M their masses. Then, energy momentum conservation
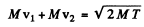
(in the frame of the stationary H atom)
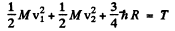
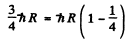 is the excitation energy of the n = 2 state from the ground state.
is the excitation energy of the n = 2 state from the ground state.
Eliminating v2
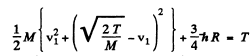
or
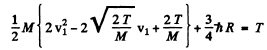
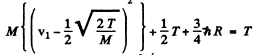
or 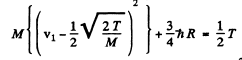
For minimum T, the square on the left should vanish. Thus 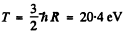
Q.41. A stationary hydrogen atom emits a photon corresponding to the first line of the Lyman series. What velocity does the atom acquire?
Ans. In the rest frame of die original excited nudeus we have the equations 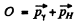
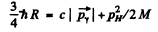
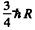 is the eneigy available in
is the eneigy available in 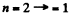 transition corresponding to the first Lyman line.)
transition corresponding to the first Lyman line.)
Then
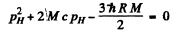
or 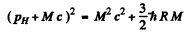
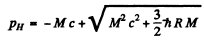
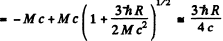
(We could have written this directly by noting that 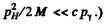 Then
Then
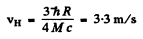
Q.42. From the conditions of the foregoing problem find how much (in per cent) the energy of the emitted photon differs from the energy of the corresponding transition in a hydrogen atom.
Ans. We have
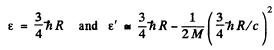
Then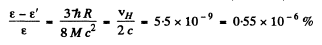
Q.43. A stationary He ion emitted a photon corresponding to the first line of the Lyman series. That photon liberated a photoelectron from a stationary hydrogen atom in the ground state. Find the velocity of the photoelectron.
Ans. We neglect recoil effebts. The energy of the first Lyman line photon emitted by He+ is
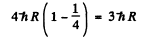
The velocity v of the photoelectron that this photon liberates is given by
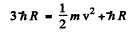
where h R on the right is the binding eneigy of the n = 1 electron in H atom. Thus
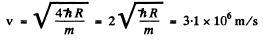
Here m is the mass of the electron.
Q.44. Find the velocity of the excited hydrogen atoms if the first line of the Lyman series is displaced by Δλ = 0.20 nm when their radiation is observed at an angle θ = 45° to their motion direction.
Ans. Since 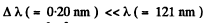 of the first Lyman line of H atom, we need not worry about
of the first Lyman line of H atom, we need not worry about 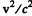 effects. Then
effects. Then
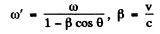
Hence 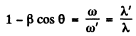
or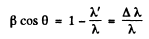
But 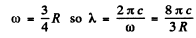
Hence 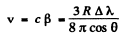
Substitution gives 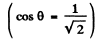
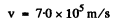
Q.45. According to the Bohr-Sommerfeld postulate the periodic motion of a particle in a potential field must satisfy the following quantization rule:
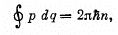
where q and p are generalized coordinate and momentum of the particle , n are integers. Making use of this rule, find the permitted values of energy for a particle of mass m moving
(a) in a unidimensional rectangular potential well of width l with infinitely high walls;
(b) along a circle of radius r;
(c) in a unidimensional potential field U = ax2/2, where a is a positive constant;
(d) along a round orbit in a central field, where the potential energy of the particle is equal to U = —α/r (α is a positive constant).
Ans. (a) If we measure eneigy from the bottom of the well, then V(x) = 0 inside the walls. Then
the quantization condition reads 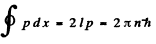
or 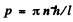
Hence 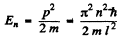
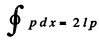 because we have to consider the integral form
because we have to consider the integral form 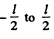 and then back to
and then back to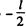
(b) Here 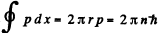
or 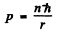
Hence 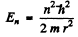
(c) By energy conservation 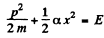
so 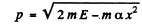
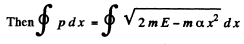
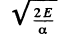
The integral is
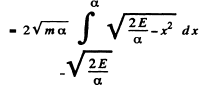
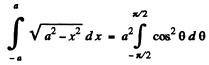
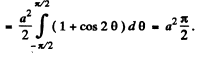
Thus 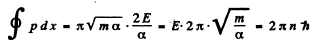
Hence 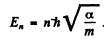
(b) It is requined to find the energy levels of the circular orbait for the rotential
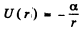
In a circular orbit, the particle only has tangential velocity and the quantization condition read 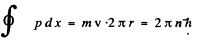
so 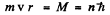
The energy of the particle is
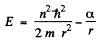
Equilibrium requires that the energy as a function of r be minimum. Thus
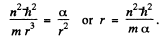
Hence 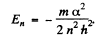
Q.46. Taking into account the motion of the nucleus of a hydrogen atom, find the expressions for the electron's binding energy in the ground state and for the Rydberg constant. How much (in per cent) do the binding energy and the Rydberg constant, obtained without taking into account the motion of the nucleus, differ from the more accurate corresponding values of these quantities?
Ans. The total energy of the H-atom in an arbitrary frame is
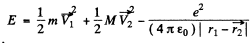
Here 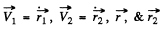 are the coordinates of the electron and protons.
are the coordinates of the electron and protons.
We define
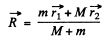
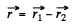
Then 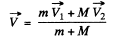
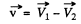
or 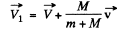
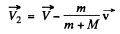
and we get 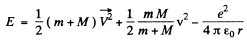
In the frame 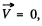 this reduces to the energy of a particle of mass
this reduces to the energy of a particle of mass
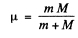
μ is called the reduced mass.
Then 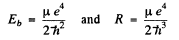
Since 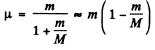
these values differ by 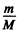 (= 0.54%) from the values obtained without considering nuclear motion (M = 1837m)
(= 0.54%) from the values obtained without considering nuclear motion (M = 1837m)
Q..47. For atoms of light and heavy hydrogen (H and D) find the difference
(a) between the binding energies of their electrons in the ground state;
(b) between the wavelengths of first lines of the Lyman series.
Ans. The difference between the binding energies is
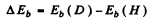
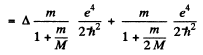
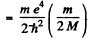
Substitution gives . 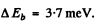
For the first line of the Lyman series
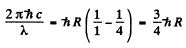
or 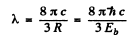
Hence
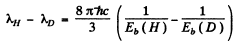
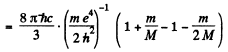
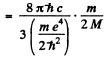
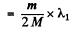
(where λ1 is the wavelength of the first line of Lyman series without considering nuclear motion).
Substitution gives (see 6.21 for using λ1 = 121 nm
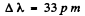
Q.48. Calculate the separation between the particles of a system in the ground state, the corresponding binding energy, and the wavelength of the first line of the Lyman series, if such a system is
(a) a mesonic hydrogen atom whose nucleus is a proton (in a mesonic atom an electron is replaced by a meson whose charge is the same and mass is 207 that of an electron);
(b) a positronium consisting of an electron and a positron revolving around their common centre of masses.
Ans. (a) In the mesonic system, the reduced mass of the system is related to the masses of the meson (mμ) and proton (mp) by
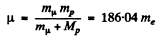
Then,
separation between the particles in the ground state 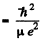
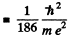
= 0.284 pm
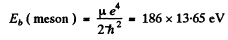
= 2.54 keV
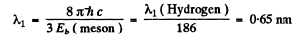
(on using λ1 (Hydrogen) =121nm).
(b) In the positronium
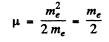
Thus separation between the particles is the ground state
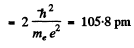
Eb(positronium) 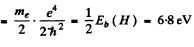
λ1 (positronium) = λ2 (Hydrogen) = 0.243 nm
FAQs on Irodov Solutions: Scattering of Particles: Rutherford-Bohr Atom - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the Rutherford-Bohr model of the atom? |  |
| 2. How does the Rutherford-Bohr model explain the scattering of particles? |  |
| 3. What is the significance of the Rutherford-Bohr model in understanding atomic structure? |  |
| 4. How does the Rutherford-Bohr model relate to the quantization of energy? |  |
| 5. What are the limitations of the Rutherford-Bohr model? |  |
















