The number 1 is special because it has only one factor, which is itself. It doesn’t meet the criteria to be classified as either a prime number (which has exactly two factors) or a composite number (which has more than two factors).
Class 6 Exam > Class 6 Notes > Mathematics (Maths) Class 6 > Worksheet Solutions: Playing with Numbers - 1
Playing with Numbers - 1 Class 6 Worksheet Maths
Q1: Fill ups:
(i) The numbers which have more than two factors are called ________.
Ans: Composite
A composite number has more than two factors. For example, 4 is a composite number because it has factors 1, 2, and 4.
(ii) The numbers which are not multiples of 2 are known as ________.
Ans: Odd
Odd numbers cannot be divided evenly by 2. For example, 3 and 7 are odd numbers because they don’t divide by 2 without leaving a remainder.
(iii) The two numbers which have only 1 as their common factor are called _________.
Ans: Co-primes
Co-prime numbers have no common factors other than 1. For instance, 8 and 15 are co-prime because 1 is their only common factor.
(iv) The number which is neither prime nor composite is _____.
Ans: 1
(v) Every number is a ________ and ________ of itself.
Ans: Factor, Multiple
Every number can divide itself exactly (making it a factor of itself) and can also be multiplied by 1 to get itself (making it a multiple of itself). For example, 5 is both a factor and a multiple of 5.
Q2: True or False:
(i) The sum of three odd numbers is even.
Ans: False
3 + 5 + 7 = 15, i.e., odd
(ii) The sum of two odd numbers and one even number is even.
Ans: True
3 + 5 + 6 = 14, i.e., even
(iii) The product of three odd numbers is odd.
Ans: True
3 x 5 x 7 = 105, i.e., odd
(iv) If an even number is divided by 2, the quotient is always odd.
Ans: False
4 ÷ 2 = 2, i.e., even
(v) All prime numbers are odd.
Ans: False
2 is a prime number and it is also even
(vi) Prime numbers do not have any factors.
Ans: False
1 and the number itself are factors of the number
(vii) The sum of two prime numbers is always even.
Ans: False
2 + 3 = 5, i.e., odd
(viii) 2 is the only even prime number.
Ans: True
(ix) All even numbers are composite numbers.
Ans: False
2 is a prime number
(x) The product of two even numbers is always even.
Ans: True
2 x 4 = 8, i.e., even
Q3: Answer the following Questions.
(i) Find all the multiples of 13 up to 100.
Ans: 13, 26, 39, 52, 65, 78, 91
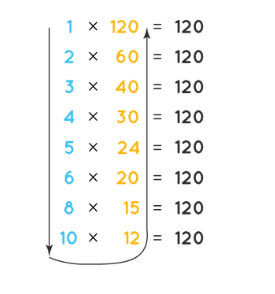
(ii) Write all the factors of 120.
Ans: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
(iii) Identify the numbers below which are multiples of 45.
270, 295, 305, 315, 333, 360, 400
Ans: 270, 315, 360
(iv) The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers up to 100.
Ans: 17, 71
37, 73
79, 97
(v) Write down separately the prime and composite numbers less than 20.
Ans: Prime numbers less than 20 are
2, 3, 5, 7, 11, 13, 17, 19
Composite numbers less than 20 are
4, 6, 8, 9, 10, 12, 14, 15, 16, 18
(vi) What is the greatest prime number between 1 and 10?
Ans: Prime numbers between 1 and 10 are 2, 3, 5, and 7. Among these numbers, 7 is the greatest.
(vii) Express the following as the sum of two odd primes.
(a) 44
(b) 36
(c) 24
(d) 18
Ans: (a) 44 = 37 + 7
(b) 36 = 31 + 5
(c) 24 = 19 + 5
(d) 18 = 11 + 7
(viii) Write seven consecutive composite numbers less than 100 so that there is no prime number between them.
Ans: Between 89 and 97, both of which are prime numbers, there are 7 composite numbers. They are
90, 91, 92, 93, 94, 95, 96
Numbers Factors:
- 90 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
- 91 = 1, 7, 13, 91
- 92 = 1, 2, 4, 23, 46, 92
- 93 = 1, 3, 31, 93
- 94 = 1, 2, 47, 94
- 95 = 1, 5, 19, 95
- 96 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
(ix) Write a digit in the blank space of each of the following numbers so that the number formed is divisible by 11:
(a) 92 ___ 389
(b) 8 ___9484
Ans:
(a) 92_389
Let a be placed in the blank.
Sum of the digits at odd places = 9 + 3 + 2 = 14
Sum of the digits at even places = 8 + a + 9 = 17 + a
Difference = 17 + a − 14 = 3 + a
For a number to be divisible by 11, this difference should be zero or a multiple of 11.
If 3 + a = 0, then
a = − 3
However, it cannot be negative.
The closest multiple of 11, which is near to 3, has to be taken. It is 11 itself.
3 + a = 11
a = 8
Therefore, the required digit is 8.
(b) 8_9484
Let a be placed in the blank.
Sum of the digits at odd places = 4 + 4 + a = 8 + a
Sum of the digits at even places = 8 + 9 + 8 = 25
Difference = 25 − (8 + a)
= 17 − a
For a number to be divisible by 11, this difference should be zero or a multiple of 11.
If 17 − a = 0, then
a = 17
This is not possible.
A multiple of 11 has to be taken. Taking 11, we obtain
17 − a = 11
a = 6
Therefore, the required digit is 6.
(x) A number is divisible by both 5 and 12. By which another number will that number be always divisible?
Ans: Factors of 5 = 1, 5
Factors of 12 = 1, 2, 3, 4, 6, 12
As the common factor of these numbers is 1, the given two numbers are co-prime and the number will also be divisible by their product, i.e. 60, and the factors of 60, i.e., 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
(xi) A number is divisible by 12. By what other number will that number be divisible?
Ans: Since the number is divisible by 12, it will also be divisible by its factors i.e., 1, 2, 3, 4, 6, 12. Clearly, 1, 2, 3, 4, and 6 are numbers other than 12 by which this number is also divisible.
(xii) The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.
Ans: 2 * 3 * 4 = 24, which is divisible by 6
9 * 10 * 11 = 990, which is divisible by 6
20 * 21 * 22 = 9240, which is divisible by 6
(xiii) The sum of two consecutive odd numbers is divisible by 4. Verify this statement with the help of some examples.
Ans: 3 + 5 = 8, which is divisible by 4
15 + 17 = 32, which is divisible by 4
19 + 21 = 40, which is divisible by 4
(xiv) Determine if 25110 is divisible by 45.
[Hint: 5 and 9 are co-prime numbers. Test the divisibility of the number by 5 and 9].
Ans: 45 = 5 * 9
Factors of 5 = 1, 5
Factors of 9 = 1, 3, 9
Therefore, 5 and 9 are co-prime numbers.
Since the last digit of 25110 is 0, it is divisible by 5.
Sum of the digits of 25110 = 2 + 5 + 1 + 1 + 0 = 9
As the sum of the digits of 25110 is divisible by 9, therefore, 25110 is divisible by 9.
Since the number is divisible by 5 and 9 both, it is divisible by 45.
(xv) Find the LCM of 12, 16, 24 and 36?
Ans:
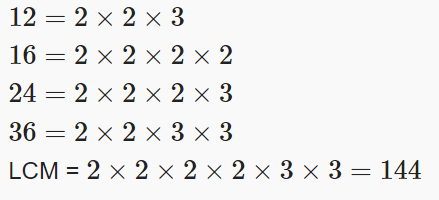
(xvi) Find the HCF of 70, 105, 175
Ans:
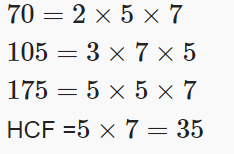
(xvii) You have 24 small bottles of lemonade and 36 large bottles. What is the largest number of equal-sized groups you can make if each group has the same number of small and large bottles?
Ans: 24 small bottles and 36 large bottles
HCF of 24 and 36 = 12
Largest number of equal-sized groups = 12
The document Playing with Numbers - 1 Class 6 Worksheet Maths is a part of the Class 6 Course Mathematics (Maths) Class 6.
All you need of Class 6 at this link: Class 6
|
92 videos|348 docs|54 tests
|
FAQs on Playing with Numbers - 1 Class 6 Worksheet Maths
| 1. What are prime numbers? |  |
Ans. Prime numbers are numbers that are greater than 1 and can only be divided by 1 and themselves without leaving a remainder.
| 2. How can we determine if a number is even or odd? | |
Ans. A number is even if it can be divided by 2 without leaving a remainder, and it is odd if it cannot be divided by 2 without leaving a remainder.
| 3. How can we find the factors of a number? | |
Ans. To find the factors of a number, we can divide the number by different numbers starting from 1 up to the number itself, and the numbers that divide the original number without leaving a remainder are its factors.
| 4. What is the significance of multiples of a number? | |
Ans. Multiples of a number are the result of multiplying that number by other whole numbers. Understanding multiples helps in finding patterns in numbers and solving mathematical problems efficiently.
| 5. How is the concept of divisibility important in mathematics? | |
Ans. Divisibility rules help in determining if a number can be divided by another number without leaving a remainder. This concept is crucial in various mathematical operations and problem-solving strategies.
Related Exams
About this Document
|
18.8K Views |
|
4.72/5 Rating |
|
Dec 22, 2024 Last updated |
Document Description: Worksheet Solutions: Playing with Numbers - 1 for Class 6 2024 is part of Mathematics (Maths) Class 6 preparation.
The notes and questions for Worksheet Solutions: Playing with Numbers - 1 have been prepared according to the Class 6 exam syllabus. Information about Worksheet Solutions: Playing with Numbers - 1 covers topics
like and Worksheet Solutions: Playing with Numbers - 1 Example, for Class 6 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Worksheet Solutions: Playing with Numbers - 1.
Introduction of Worksheet Solutions: Playing with Numbers - 1 in English is available as part of our Mathematics (Maths) Class 6
for Class 6 & Worksheet Solutions: Playing with Numbers - 1 in Hindi for Mathematics (Maths) Class 6 course.
Download more important topics related with notes, lectures and mock test series for Class 6
Exam by signing up for free. Class 6: Playing with Numbers - 1 Class 6 Worksheet Maths
Description
Full syllabus notes, lecture & questions for Playing with Numbers - 1 Class 6 Worksheet Maths - Class 6 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 6 | Best notes, free PDF download
Information about Worksheet Solutions: Playing with Numbers - 1
In this doc you can find the meaning of Worksheet Solutions: Playing with Numbers - 1 defined & explained in the simplest way possible. Besides explaining types of
Worksheet Solutions: Playing with Numbers - 1 theory, EduRev gives you an ample number of questions to practice Worksheet Solutions: Playing with Numbers - 1 tests, examples and also practice Class 6
tests
|
Explore Courses for Class 6 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Semester Notes
,MCQs
,Objective type Questions
,Playing with Numbers - 1 Class 6 Worksheet Maths
,study material
,Previous Year Questions with Solutions
,Sample Paper
,Viva Questions
,ppt
,Playing with Numbers - 1 Class 6 Worksheet Maths
,shortcuts and tricks
,Summary
,Playing with Numbers - 1 Class 6 Worksheet Maths
,Exam
,mock tests for examination
,past year papers
,Important questions
,video lectures
,Extra Questions
,practice quizzes
,Free
;
Additional Information about Worksheet Solutions: Playing with Numbers - 1 for Class 6 Preparation
Worksheet Solutions: Playing with Numbers - 1 Free PDF Download
The Worksheet Solutions: Playing with Numbers - 1 is an invaluable resource that delves deep into the core of the Class 6 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Worksheet Solutions: Playing with Numbers - 1 now and kickstart your journey towards success in the Class 6 exam.
Importance of Worksheet Solutions: Playing with Numbers - 1
The importance of Worksheet Solutions: Playing with Numbers - 1 cannot be overstated, especially for Class 6 aspirants.
This document holds the key to success in the Class 6 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Worksheet Solutions: Playing with Numbers - 1 Notes
Worksheet Solutions: Playing with Numbers - 1 Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Worksheet Solutions: Playing with Numbers - 1.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Worksheet Solutions: Playing with Numbers - 1 Notes on EduRev are your ultimate resource for success.
Worksheet Solutions: Playing with Numbers - 1 Class 6 Questions
The "Worksheet Solutions: Playing with Numbers - 1 Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Worksheet Solutions: Playing with Numbers - 1 on the App
Students of Class 6 can study Worksheet Solutions: Playing with Numbers - 1 alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Worksheet Solutions: Playing with Numbers - 1,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Worksheet Solutions: Playing with Numbers - 1 is prepared as per the latest Class 6 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup