Irodov Solutions: Motion of Charged Particles In Electric And Magnetic Fields- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 372. At the moment t = 0 an electron leaves one plate of a parallel-plate capacitor with a negligible velocity. An accelerating voltage, varying as V = at, where a = 100 V/s, is applied between the plates. The separation between the plates is l = 5.0 cm. What is the velocity of the electron at the moment it reaches the opposite plate?
Solution. 372. Let the electron leave the negative plate of the capacitor at time t = 0
As ’ 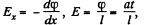
and, therefore, the acceleration of the electron,
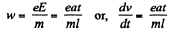
or, 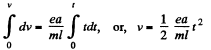 (1)
(1)
But, from 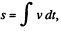
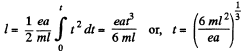
Putting the value of t in (1),
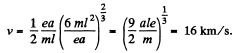
Q. 373. A proton accelerated by a potential difference V gets into the uniform electric field of a parallel-plate capacitor whose plates extend over a length 1 in the motion direction. The field strength varies with time as E = at, where a is a constant. Assuming the proton to be non-relativistic, find the angle between the motion directions of the proton before and after its flight through the capacitor; the proton gets in the field at the moment t = 0. The edge effects are to be neglected.
Solution. 373. The electric field inside the capacitor varies with time as,
E = at.
Hence, electric force on the proton,
F = eat
and subsequently, acceleration of the proton,
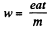
Now, if t is the time elapsed during the motion of the proton between the plates, then 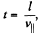 as no acceleration is effective in this direction.
as no acceleration is effective in this direction. 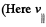 is velocity along the length of the plate.)
is velocity along the length of the plate.)
From kinematics, 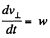
so, 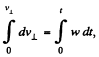
(as initially, the component of velocity in the direction, ⊥ to plates, was zero.)
or 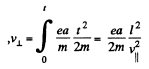
Now, 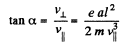
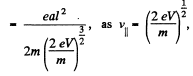 from energy conservation.
from energy conservation.
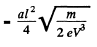
Q. 374. A particle with specific charge qlm moves rectilinearly due to an electric field E = E0 — ax, where a is a positive constant, x is the distance from the point where the particle was initially at rest. Find:
(a) the distance covered by the particle till the moment it came to a standstill;
(b) the acceleration of the particle at that moment.
Solution. 374. The equation of motion is,
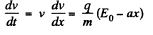
Integrating
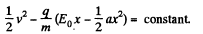
But initially v = 0 when x = 0, so “constant” = 0
Thus, 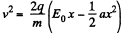
Thus.v = 0, again for 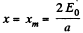
The corresponding acceleration is,
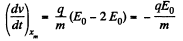
Q. 375. An electron starts moving in a uniform electric field of strength E = 10 kV/cm. How soon after the start will the kinetic energy of the electron become equal to its rest energy?
Solution. 375. From the law of relativistic conservation of energy
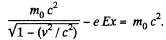
as the electron is at rest (v = 0 for x = 0) initially.
Thus clearly T = eEx.
On the other hand, 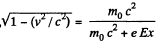
or, 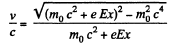
or, 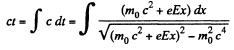
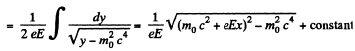
The “constant” = 0, at t = 0, for x = 0,
So, 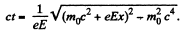
Finally, using T = eEx,
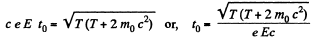
Q. 376. Determine the acceleration of a relativistic electron moving along a uniform electric field of strength E at the moment when its kinetic energy becomes equal to T.
Solution. 376. As before, T = e E x
Now in linear motion,
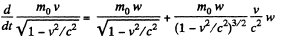
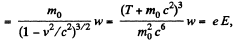
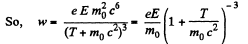
Q. 377. At the moment t = 0 a relativistic proton flies with a velocity v, into the region where there is a uniform transverse electric field of strength E, with v0 ⊥ E. Find the time dependence of
(a) the angle θ between the proton's velocity vector v and the initial direction of its motion;
(b) the projection vx of the vector v on the initial direction of motion.
Solution. 377. The equations are,
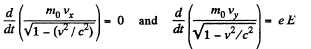
Hence, 
Also, by energy conservation,
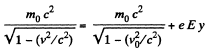
Dividing 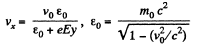
Also, 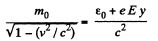
Thus, 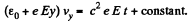
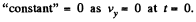
Integrating again,
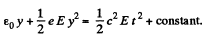
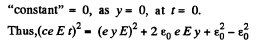
or, 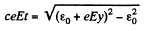
or, 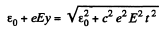
Hence, 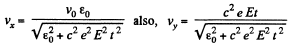
and 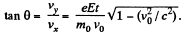
Q. 378. A proton accelerated by a potential difference V = 500 kV flies through a uniform transverse magnetic field with induction B = 0.51 T. The field occupies a region of space d =10 cm in thickness (Fig. 3.99). Find the angle α through which the proton deviates from the initial direction of its motion.
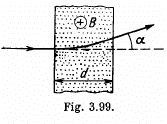
Solution. 378. From the figure,
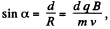
As radius of the arc 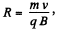 where v is the velocity of the particle, when it enteres into the field. From initial condition of the problem,
where v is the velocity of the particle, when it enteres into the field. From initial condition of the problem,
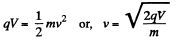
Hence, 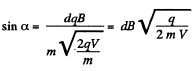
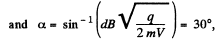 on putting the values.
on putting the values.
Q. 379. A charged particle moves along a circle of radius r = 100 mm in a uniform magnetic field with induction B = 10.0 mT. Find its velocity and period of revolution if that particle is
(a) a non-relativistic proton;
(b) a relativistic electron.
Solution. 379. (a) For motion along a circle, the magnetic force acted on the particle, will provide the centripetal force, necessary for its circular motion.
i.e. 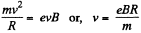
and the period of revolution 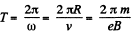

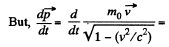
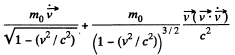
For transverse motion, 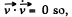
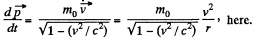
Thus, 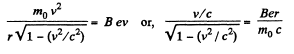
or, 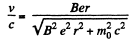
Finally, 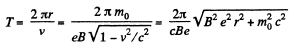
Q. 380. A relativistic particle with charge q and rest mass m0 moves along a circle of radius r in a uniform magnetic field of induction B. Find:
(a) the modulus of the particle's momentum vector;
(b) the kinetic energy of the particle;
(c) the acceleration of the particle.
Solution. 380. (a) As before,p = B qr.
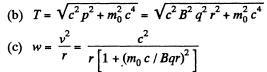
using the result for v from the previous problem.
Q. 381. Up to what values of kinetic energy does the period of revolution of an electron and a proton in a uniform magnetic field exceed that at non-relativistic velocities by η = 1.0 % ?
Solution. 381. From (Q.279),
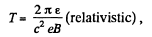
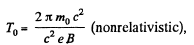
Here, 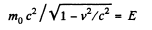
Here, 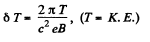
Now, 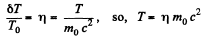
Q. 382. An electron accelerated by a potential difference V = 1.0 kV moves in a uniform magnetic field at an angle α = 30° to the vector B whose modulus is B = 29 mT. Find the pitch of the helical trajectory of the electron.
Solution. 382.
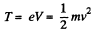
(The given potential difference is not large enough to cause significant deviations from the nonrelativistic formula).
Thus, 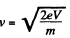
So, 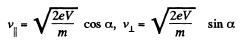
Now, 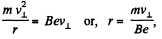
and 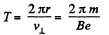
Pitch 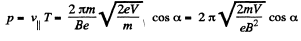
Q. 383. A slightly divergent beam of non-relativistic charged particles accelerated by a potential difference V propagates from a point A along the axis of a straight solenoid. The beam is brought into focus at a distance l from the point A at two successive values of magnetic induction B1 and B2. Find the specific charge q/m of the particles.
Solution. 383. The charged particles will traverse a helical trajectory and will be focussed on the axis after traversing a number of turms. Thus
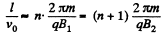
So, 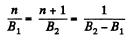
Hence, 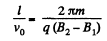
or, 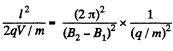
or, 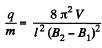
Q. 384. A non-relativistic electron originates at a point A lying on the axis of a straight solenoid and moves with velocity v at an angle α to the axis. The magnetic induction of the field is equal to B. Find the distance r from the axis to the point on the screen into which the electron strikes. The screen is oriented at right angles to the axis and is located at a distance l from the point A.
Solution. 384. Let us take the point A as the origin O and the axis of the solenoid as z-axis. At an arbitrary moment of time let us resolve the velocity of electron into its two rectangular components, 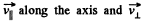 to the axis of solenoid. We know the magnetic force does no work, so the kinetic energy as well as the speed of the electron
to the axis of solenoid. We know the magnetic force does no work, so the kinetic energy as well as the speed of the electron 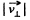 will remain constant in the x-y plane. Thus
will remain constant in the x-y plane. Thus 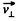 can change only its direction as shown in the Fig..
can change only its direction as shown in the Fig.. 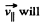 remain constant as it is parallel to
remain constant as it is parallel to 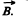
Thus at t = t
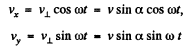
and 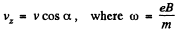
As at r = 0, we have x = y = z = 0, so the motion law of the electron is.
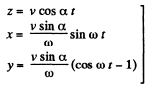
(The equation of the helix)
On the screen, 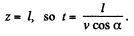
Then, 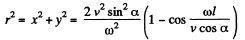
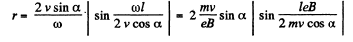
Q. 385. From the surface of a round wire of radius a carrying a direct current I an electron escapes with a velocity vo perpendicular to the surface. Find what will be the maximum distance of the electron from the axis of the wire before it turns back due to the action of the magnetic field generated by the current.
Solution. 385. Choose the wire along the z-axis, and the initial direction of the electron, along the x-axis. Then the magnetic field in the x - z plane is along the y - axis and outside the wire it is,
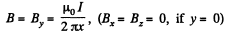
The motion must b e confined to the x - z plane. Then the equations o f motion are,
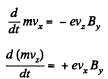
Multiplying the first equation by vx and the second by vz and then adding,
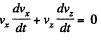
or, 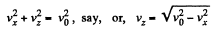
Then, 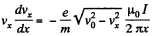
or, 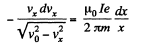
Integrating, 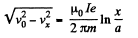
on using,vx = v0 , if x = a (i.e. initially).
Now, 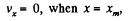
so, 
Q. 386. A non-relativistic charged particle flies through the electric field of a cylindrical capacitor and gets into a uniform transverse magnetic field with induction B (Fig. 3.100). In the capacitor the particle moves along the arc of a circle, in the magnetic field, along a semi-circle of radius r. The potential difference applied to the capacitor is equal to V, the radii of the electrodes are equal to a and b, with a < b. Find the velocity of the particle and its specific charge q/m.
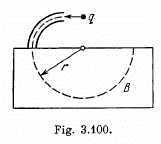
Solution. 386. Inside the capacitor, the electric field follows 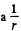 law, and so the potential can be written as
law, and so the potential can be written as
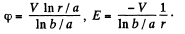
Here r is the distance from the axis of the capacitor.
Also, 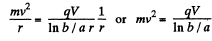
On the other hand,
mv = q B r in the magnetic field.
Thus, 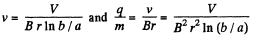
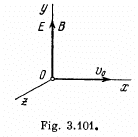
Q. 387. Uniform electric and magnetic fields with strength E and induction B respectively are directed along the y axis (Fig. 3.101). A particle with specific charge q/m leaves the origin O in the direction of the x axis with an initial non-relativistic velocity v0. Find:
(a) the coordinate yn of the particle when it crosses the y axis for the nth time;
(b) the angle α between the particle's velocity vector and the y axis at that moment.
Solution. 387. The equations of motion are,
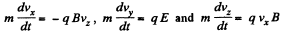
These equations can be solved easily.
First, 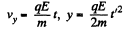
Then, 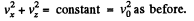
In fact, vx = v0 cos ωt and vz - v0 sin cor as one can check.
Integrating again and using x = z = 0, at t = 0
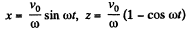
Thus, 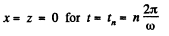
At that instant, 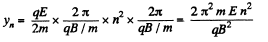
Also, 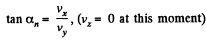
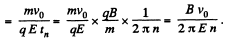
Q. 388. A narrow beam of identical ions with specific charge q/m, possessing different velocities, enters the region of space, where there are uniform parallel electric and magnetic fields with strength E and induction B, at the point O (see Fig. 3.101). The beam direction coincides with the x axis at the point O. A plane screen oriented at right angles to the x axis is located at a distance l from the point O. Find the equation of the trace that the ions leave on the screen. Demonstrate that at z ≪ l it is the equation of a parabola.

Solution. 388. The equation of the trajectory is,
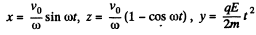 as before see (Q.384).
as before see (Q.384).
Now on the screen x = l, so
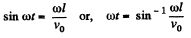
At that moment,
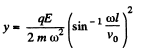
so, 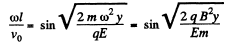
and 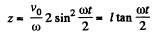
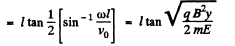
For small
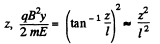
or, 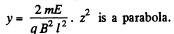
FAQs on Irodov Solutions: Motion of Charged Particles In Electric And Magnetic Fields- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the motion of charged particles in electric and magnetic fields? |  |
| 2. How does the motion of a charged particle change when it enters an electric field? |  |
| 3. How does the motion of a charged particle change when it enters a magnetic field? |  |
| 4. What is the relationship between the velocity of a charged particle and the radius of its path in a magnetic field? |  |
| 5. How is the motion of a charged particle affected when it enters both an electric and magnetic field simultaneously? |  |
















