Lakhmir Singh & Manjit Kaur: Electricity, Solutions- 3 | Science Class 10 PDF Download
Page No:38
Question 8:
Show how you would connect two 4 ohm resistors to produce a combined resistance of
(a) 2 ohms
(b) 8 ohms.
Solution :
(a) By connecting in parallel: Since equivalent resistance will be
1/ R = 1/4 + 1/4 = 2/4 = 1/2
Therefore, R = 2 ohm
(b) By connecting in series : Since equivalent resistance will be
R = 4 ohm + 4 ohm = 8 ohm.
Question 9:
Which of the following resistor arrangement, A or B, has the lower combined resistance ?
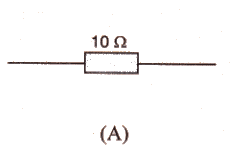
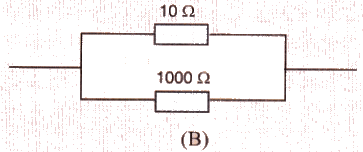
Solution :
Resistance of arrangement A is 10 ohm.
Combined resistance of arrangement B is caculated as follows:
1/R = 1/10 + 1/1000 = (100+1)/1000
R = 1000/101 = 9.9 ohm
Therefore, arrangement B has lower combined resistance.
Question 10:
A wire that has resistance R is cut into two equal pieces. The two parts are joined in parallel. What is the resistance of the combination ?
Solution :
Resistance of each part is R/2.
Resultant resistance R’ is given by
1/R’ = 2/R+2/R
R’=R/4.
Question 11:
Calculate the combined resistance in each case :
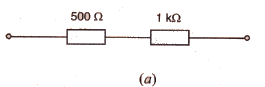
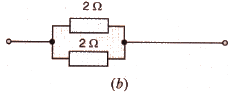
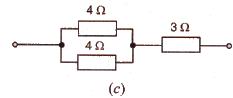
Solution :



Question 12:
Find the current in each resistor in the circuit shown below :
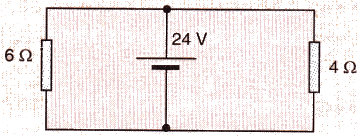
Solution :

Question 13:
Explain with diagrams what is meant by the “series combination” and “parallel combination” of resistances. In which case the resultant resistance is : (i) less, and (ii) more, than either of the individual resistances ?
Solution :
(i) Series combination
When two or more resistances are connected end to end consecutively, they are said to be connected In series combination. The combined resistance of any number of resistances connected in series in equal to the sum of the individual resistances.
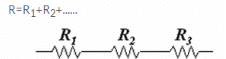
The resultant resistance is more than either of the Individual resistances.
(ii) Parallel combination
When two or more resistances are connected between the same two points, they are said to be connected in parallel combination. The reciprocal of the combined resistance of a number of resistances connected In parallel Is equal to the sum of the reciprocals of all the Individual resistances.
Question 14:
A battery of 9 V is connected in series with resistors of 0.2 Ω, 0.3 Ω, 0.4 Ω, 0.5 Ω and 12 Ω. How much current would flow through the 12 Ω resistor ?
Solution :
R1 = 0.2ohm, R2 = 0.4ohm, R3 = 0.3ohm,R4 = 0.5ohm. R5 =12ohm, V = 9V
Resultant resistance = R1+ R2+ R3+ R4+ R5
R = 0.2+0.4+0.3+0.5+12 =13.4ohm
Thus the current flow through 12ohm resistance will be.V/R
I = 9/13.4
I = 0.67amp.
Question 15:
An electric bulb of resistance 20 Ω and a resistance wire of 4 Ω are connected in series with a 6 V battery. Draw the circuit diagram and calculate :
(a) total resistance of the circuit.
(b) current through the circuit.
(c) potential difference across the electric bulb.
(d) potential difference across the resistance wire.
Solution :
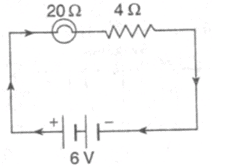
(a) Total resistance of the circuit=R1-FR2=20+4=24ohm
(b) We know that
V = I R
Therefore.
6 = 1 x 24
I = 6/24 = 0.25amp
(c) p.d. across bulb = I R1= 0.25X20 = 5V
(d) p.d. across resistance wire= I R2 = 0.25X4 = 1V
Question 16:
Three resistors are connected as shown in the diagram.
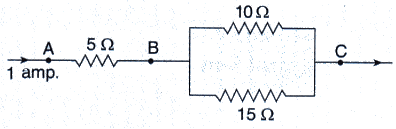
Through the resistor 5 ohm, a current of 1 ampere is flowing,
(i) What is the current through the other two resistors ?
(ii) What is the p.d. across AB and across AC ?
(iii) What is the total resistance ?
Solution :
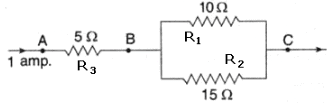
According to the diagram.
(i) Total current I = 1 amp is entering the parallel combination of R1 and R2. Let I1 current flow through R1 and I2 current flow through R2. Then
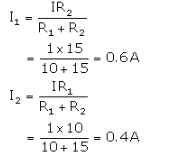
(ii) p.d. across AB - IR3 = 1 x 5 - 5V
Equivalent resisyance between B and C is
1/R' = 1/R1 + 1/R2 = 1/10 + 1/15
1/R' = 5/30
R' - 6 ohm
Total resistance between A and C is R = 5-6 = 11 ohm p.d. across AC = IR = 1x11= 11V
(iii) Total resistance = R3 + R' = 5+ 6 =11 ohm
Question 17:
For the circuit shown in the diagram below :
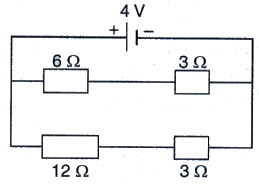
What is the value of :
(i) current through 6 Ωresistor ?
(ii) potential difference across 12 Ω resistor ?
Solution :
As per the circuit V = 4 V
Total resistance in line 1 = R1 = 6 + 3 = 9 ohm
Total resistance in line 2 = R2 = 12 + 3 = 15 ohm
(i) Current through 60 resistor = current through line 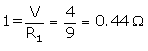
p.d. across line 2 is 4V
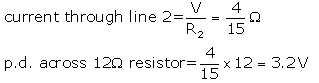
Page No:39
Question 18:
Two resistors, with resistances 5 Ω and 10 Ω respectively are to be connected to a battery of emf 6 V so as to obtain :
(i) minimum current flowing (ii) maximum current flowing
(a) How will you connect the resistances in each case ? .
(b) Calculate the strength of the total current in the circuit in the two cases.
Solution :
Given: Two resistors with resistances R1=5ohm and R2=10ohm, V=6volt
(a) For minimum current these two should be connected in series. For maximum current these two should be connected in parallel.
(b)In series,
Total resistance = 5+10 = 15ohms
Therefore total current drawn = V/R = 6/15 = 0.4amps
In parallel,
Total resistance R is given as
1/R=1/R1+1/R2
1/R=1/5+1/10
1/R=3/10
R=10/3ohm
Therefore total current drawn by the circuit = V/R = 6/(10/3) =1.8amps.
Question 19:
The circuit diagram given below shows the combination of three resistors R1 R2 and R3 :
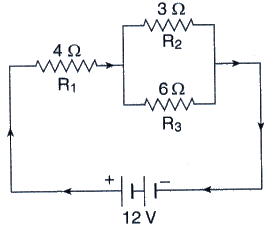
Find : (i) total resistance of the circuit.
(ii) total current flowing in the circuit.
(iii) the potential difference across R1.
Solution :
(i) Total resistance of two resistors that are connected in parallel is
1/R’ = 1/3+1/6
1/R’ = 3/6
R’ = 2ohms
Total resistance of the circuit = 2+4ohms = 6ohms
(ii) Total current flowing through the circuit=V/total resistance
I = 12/6 = 2amps
(iii) Potential difference across R1=R1 x I = 4 x 2 = 8V.
Question 20:
In the circuit diagram given below, the current flowing across 5 ohm resistor is 1 amp. Find the current flowing through the other two resistors.
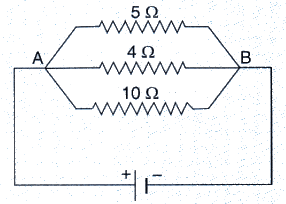
Solution :
Given :-
1 amp current is flowing through 5ohm resistor.
We know that in case of parallel connection, the p.d. across each resistor is same and is equal to the voltage applied.
Therefore, applied voltage, V = IR = 1 x 5 = 5V
So,
Current through 4 ohm resistor = V/R = 5/4 = 1.25 A
Current through 10 ohm resistor = V/R = 5/10 = 0.5 A
Question 21:
A resistor has a resistance of 176 ohms. How many of these resistors should be connected in parallel so that their combination draws a current of 5 amperes from a 220 volt supply line ?
Solution :
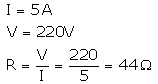
Required resistance is less than 176Ω, so the resistors should be connected in parallel. Let the required no. be n.
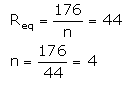
Question 22:
An electric heater which is connected to a 220 V supply line has two resistance coils A and B of 24 Ω resistance each. These coils can be used separately (one at a time), in series or in parallel. Calculate the current drawn when :
(a) only one coil A is used.
(b) coils A and B are used in series.
(c) coils A and B are used in parallel.
Solution :
Given V = 220V
RA = RB = 24 ohm
(a) Current drawn when only coils A and B used :
I = V/RA = 220/24
= 9.16amps
(b) Current drawn when coils A and B are used in series:
Total resistance. R = RA + RB = 24+24 = 48ohms
I = V/R = 220/48 = 4.58amps
(c) Current drawn when coils A and B are used in parallel:
Total resistance. 1/R = 1/RA + 1/RB = 1/24 + 1/24 = 2/24 = 1/12
R = 12ohms
I = V/R = 220/12
= 18.33amps
Question 23:
In the circuit diagram given below five resistances of 10 Ω, 40 Ω, 30 Ω, 20 Ω and 60 Ω are connected as shown to a 12 V battery.
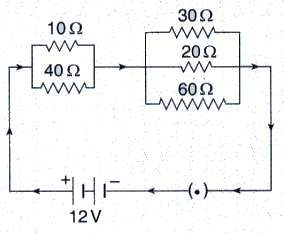
Calculate :
(a) total resistance in the circuit.
(b) total current flowing in the circuit.
Solution :
(i) Equivalent resistance of 10 Ω and 40 Ω reistances (connected in parallel) is R1, given as:
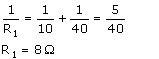
Equivalent resistance of 30Ω, 20 Ω and 60 Ω reistances (connected in parallel) is R2, given as :
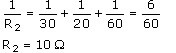
R1 and R2 are connected in series.
∴ Total resistance in the circuit is R = R1 + R2 = 8 + 10 = 18 Q
(ii) Total current flowing in the circuit,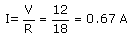
Page No:40
Question 24:
In the circuit diagram given below, three resistors R1, R2, and R3 of 5 Ω, 10 Ω and 30 Ω, respectively are connected as shown.
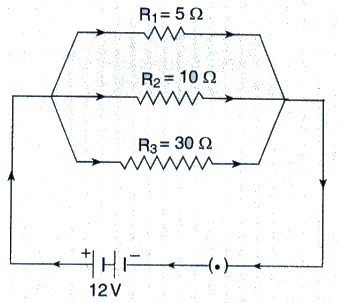
Calculate :
(a) current through each resistor.
(b) total current in the circuit.
(c) total resistance in the circuit.
Solution :
V = 12V
R1, R2 and R3 are connected in parallel.
(a) Current through R1 = V/R1 = 12/5 = 2.4 A
Current through R2 = V/R2 = 12/10 = 1.2 A
Current through R3 = V/R2 = 12/30 = 0.4A
(b) Total current in the circuit = 2.4 + 1.2 + 0.4 = 4 A
(c) Total resistance in the circuit=R
1/R = 1/R1+ 1/R2+ 1/R3
1/R = 1/5 + 1/10 + 1/30
1/R = 10/30
R = 3 ohm
Question 25:
A p.d. of 4 V is applied to two resistors of 6 Ω and 2 Ω connected in series. Calculate :
(a) the combined resistance
(b) the current flowing
(c) the p.d. across the 6 Ω resistor
Solution :
V = 4V.
R1 = 6 ohm. R2 = 8 ohm (in series)
(a) Combined resistance. R = R1 + R2 = 6+2 = 8ohm
(b) Current flowing. I = V/R = 4/8=0.5amp
(c) p.d. across 6ohm resistor = I x R1 = 0.5 x 6 = 3 V
Question 26:
A p.d. of 6 V is applied to two resistors of 3 Ω and 6 Ω connected in parallel. Calculate :
(a) the combined resistance
(b) the current flowing in the main circuit
(c) the current flowing in the 3 Ω resistor.
Solution :
V = 6V
R1= 3 ohm. R2 = 6 ohm (in parallel)
(a) Combined resistance.
1/R = 1/R1+ 1/R2
1/R = 1/3 + 1/6 = 3/6 = 1/2
R = 2 ohm
(b) Current flowing in the main circuit. I = V/R = 6/2 = 3 A
(c) Current flowing in 3 ohm resistor = V/R1= 6/3 = 2 A
Question 27:
In the circuit shown below, the voltmeter reads 10 V.
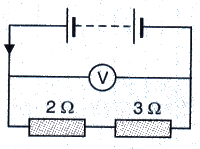
(a) What is the combined resistance ?
(b) What current flows ?
(c) What is the p.d. across 2 Ω resistor ?
(d) What is the p.d. across 3 Ω resistor ?
Solution :
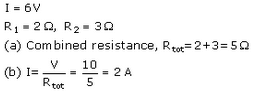
(c) p.d. across 2Ω resistor=1 xR1 = 2 x 2 = 4V
(d) p.d. across 3Ω resistor=1 x R2 = 2 x 3 = 6V
Question 28:
In the circuit given below :
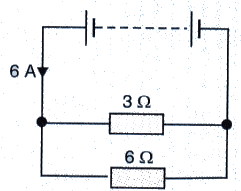
(a) What is the combined resistance ?
(b) What is the p.d. across the combined resistance ?
(c) What is the p.d. across the 3 Ω resistor ?
(d) What is the current in the 3 Ω resistor ?
(e) What is the current in the 6 Ω resistor ?
Solution :
Total current flowing through circuit. I = 6 A
R1 = 3 ohm. R2 = 6 ohm
(a) Combined resistance R is
1/R = 1/3+1/6
1/R = 3/6
R = 2ohms
(b) p.d. across the combined resistance = IR = 6 x 2 = 12 V
(c) p.d. across the 3 ohm resistor = p.d. across the combined resistance = 12 V
(d) Current flowing through the 3 ohm resistor = V/R1 = 12/3 = 4 A
(e) Current flowing through the 6 ohm resistor = V/R2 = 12/6 = 2 A
Page No:41
Question 29:
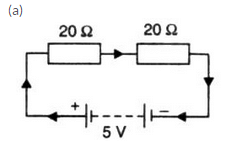
A 5 V battery is connected to two 20 Ω resistors which are joined together in series.
(a) Draw a circuit diagram to represent this. Add an arrow to indicate the direction of conventional current flow in the circuit.
(b) What is the effective resistance of the two resistors ?
(c) Calculate the current that flows from the battery.
(d) What is the p.d. across each resistor ?
Solution :

Question 30:
The figure given below shows an electric circuit in which current flows from a 6 V battery through two resistors.
(a) Are the resistors connected in series with each other or in parallel ?
(b) For each resistor, state the p.d. across it.
(c) The current flowing from the battery is shared between the two resistors. Which resistor will have bigger share of the current ?
(d) Calculate the effective resistance of the two resistors.
(e) Calculate the current that flows from the battery.
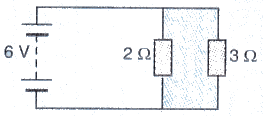
Solution :
V = 6V. R1 = 2ohms. R2 = 3ohms
(a) Resistors are connected in parallel
(b) p.d. across each resistor is same and is equal to 6V.
(c) 2 ohms resistance have bigger share of current because of its lower resistance.
(d) Effective resistance = R
1/R = 1/2+1/3
1/R = S/6
R = 1.2ohms
(e) Current flowing through battery, l = V/R = 6/1.2 = 5amps
Question 31:
A 4 Ω coil and a 2 Ω coil are connected in parallel. What is their combined resistance ? A total current of 3 A passes through the coils. What current passes through the 2 Ω coil ?
Solution : 40 and 2Ω coil are connected in parallel. Combined resistance is R
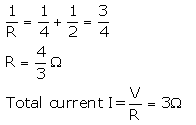
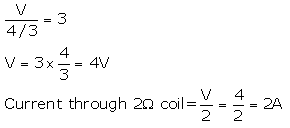
Question 32:
(a) With the help of a circuit diagram, deduce the equivalent resistance of two resistances connected in series.
(b) Two resistances are connected in series as shown in the diagram 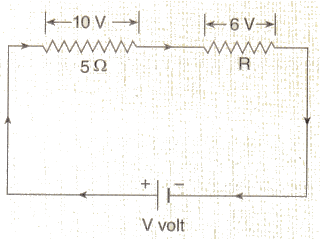
(i) What is the current through the 5 ohm resistance ?
(ii) What is the current through R ?
(iii) What is the value of R ?
(iv) What is the value of V ?
Solution :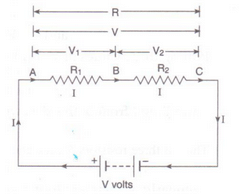
(a) Fig shows two resistances R1 and R2 connected in series with a battery of V volts.
Let the p.d. across R1 is V1 and the p.d. across R2 is V2.
S.t. V = V1 + V2 ....... (1)
Let the equivalent resistance be R and current flowing through whole circuit is I.
By Ohm's law,
V/I = R
V = I x R ---------(2)
Applying Ohm's law to both R1 end R2
V1 = I x R2 --------(3)
V2 = I X R2 ----- —(4)
From eqs. (1), (2), (3) and (4), we get
I x R = I x R1+ I x R2
I x R = I x (R1 + R2)
R = R1 + R2
(b)
(1) Current through 5Ω resisto r= 10/5 = 2A
Since 5Ω resistor and R are connected in series, so same current flows through them.
So, Current through R = 2A
(iii) V = IR
R = V/I = 6/2 = 3Ω
(iv) V = 10 + 6 = 16V
Question 33:
(a) With the help of a diagram, derive the formula for the resultant resistance of three resistors connected in series.
(b) For the circuit shown in the diagram given below :
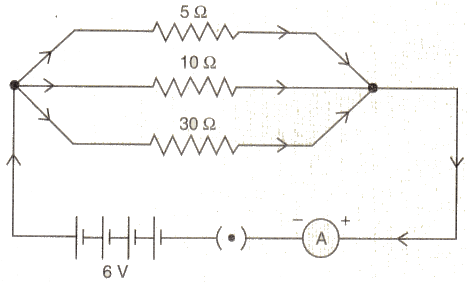
Calculate :
(i) the value of current through each resistor.
(ii) the total current in the circuit.
(iii) the total effective resistance of the circuit.
Solution :
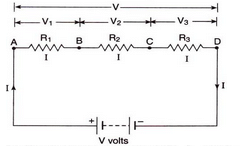
(a) Ng shows three reSistances R1, R2 and R3 ecnnected in series with a battery of V volts.
Let the p.d. across R1, R2 and R3 is V1, V2 and V3 respectively.
s.t. V = V3 + V3 + V2 ----(1)
Let the equivalent resistance be R and arrent flowing through whole circuit is I.
By Ohm's law,
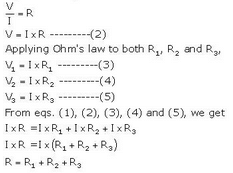
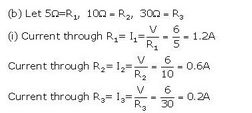
(ii) Total current in the cirait = 1.2+0.6+0.2 = 24
(iii) Effective resistance R is given as
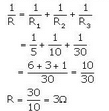
Question 34:
(a) With the help of a circuit diagram, obtain the relation for the equivalent resistance of two resistances connected in parallel.
In the circuit diagram shown below, find :
(i) Total resistance.
(ii) Current shown by the ammeter A
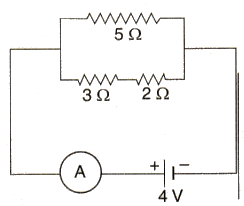
Solution :
Suppose total current flowing the circuit is I. then the current passing through resistance R1 wiII be I1 and current passing through resistance R2 will be l2 .
Total current = I = I1+I2
Let resultant resistance of this parallel combination is R. By applying the Ohm's law to the whole circuit. we get that I = V/R
Since the potential difference across the both the resistances is same. so applying the Ohm's law to each resistance we get that
I1 = V/R1
I2 = V/R2
Putting these eq in the above one, we get that
V/R = V/R1+V/R2
1/R = 1/R1+1/R2
If two resistance are connected in parallel than. the resultant resistance will be
1/R = 1/R1+1/R2
(b)
(i)Total reisitance = R
1/R=1/R1+1/R2
R2 = 3+2=5ohms
R1 = 5ohms
1/R=1/5+1/5
1/R=2/5
R=2.5ohms
Ili) Current flowing through the circuit
I = V/R = 4/(2.5)
= 1.6amps
Question 35:
(a) Explain with the help of a labelled circuit diagram, how you will find the resistance of a combination of three resistors of resistances R1, R2 and R3 joined in parallel.
(b) In the diagram shown below, the cell and the ammeter both have negligible resistance. The resistors are identical.
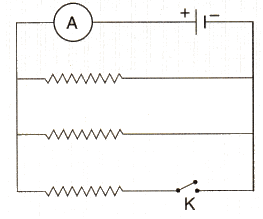
With the switch K open, the ammeter reads 0.6 A. What will be the ammeter reading when the switch is closed ?
Solution :
Suppose total current flowing in the circuit is I. then the current passing through resistance R1 will be I1 Lcurrent passing through resistance R2 will be I2 and current passing through resistance R3 will bell I3.
Total current = 1 = I1+I2+I3
Let resultant resistance of this parallel combination is R. By applying the Ohm's law to the whole circuit. we get that
I=V/R
Since the potential difference across all the resistances is same. so applying the Ohm's law to each resistance we get that
l1 = V/R1
I2 = V/R2
I3 = V/R3
Putting these eqs. in the above one. we get
V/R = V/R1V/R2+ V/R3 .
1/R = 1/R1 + 1/R2+1/R3
If two resistance are connected in parallel, then the resultant resistance will be
1/R = 1/R1+1/R2+1/R3
(b) If switch is open. then only upper two resistances (connected in parallel) are in the circuit
Effective resistance is 1/Req = 1/R+1/R = 2/R
Req = R/2
So the current.I = VA(R/2) =0.6A (given)
V/R :0.3A
When the switch closes, the third resistance also comes in the circuit. The effective resistance of the circuit becomes R/3
Hence. Current 1= V/(R/3) = 3 (V/R) = 3 x 0.3 .0.9 A
Page No:43
Question 43:
Show with the help of diagrams, how you would connect three resistors each of resistance 6 Ω, so that the combination has resistance of (i) 9 Ω (ii) 4 Ω.
Solution :
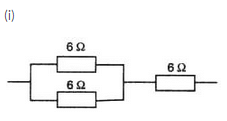
Resultant resistance for parallel circuit=R
1/R = 1/6 + 1/6
1/R = 2/6 R = 3
Effective resistance = 6 + 3 = 9ohms
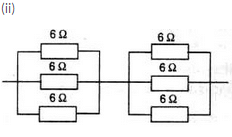
Resultant resistance for each parallel circuit= R
1/R = 1/6+1/6+1/6
1/R = 3/6
R = 2
Therefore effective resistance = 2+2 = 4ohms.
Question 44:
Two resistances when connected in parallel give resultant value of 2 ohm; when connected in series the value becomes 9 ohm. Calculate the value of each resistance.
Solution :
Two resistances when connected in series, resultant value is 9ohms.
Two resistances when connected in parallel, resultant value is 2ohms.
Let the two resistances be R1 and R2.
If connected in series, then
9 = R1+ R2
R1 = 9-R2
If connected in parallel, then
1/2 = 1/R1+1/R2
From above equations we get that
1/2=(R1+R2)/R1R2
1/2 = 9/(9-R2) R2
9R2-R22 = 18
R22-9R2+18 = 0
(R2-6) (R2-3)=0
R2 = 6,3
So if R2 = 6ohms, then R1 = 9-6 =3ohms.
If R2 = 3ohms, then R1= 9-3 = 6ohms.
Question 45:
A resistor of 8 ohms is connected in parallel with another resistor X. The resultant resistance of the combination is 4.8 ohms. What is the value of the resistor X ?
Solution :
Given:
A resistor of 8ohm is connected in parallel with a resistor of X.
And resultant is 4.8.
Then X = ?
We know that for parallel case
1/R = 1/R1+1/X
1/4.8 = 1/8+1/x
1/4.8 - 1/8 = 1/x
After solving we get that
X = 12ohms
Question 46:
You are given three resistances of 1,2 and 3 ohms. Show by diagrams, how with the help of these resistances you can get:
(i) 6 Ω (ii) [latex s=2]\frac{6}{11}[/latex] Ω (iii) 1.5 Ω
Solution :
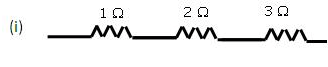 Equivalent resistance = 10 + 20 + 30 = 60
Equivalent resistance = 10 + 20 + 30 = 60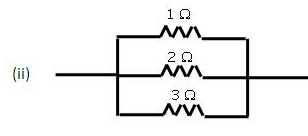 Equivalent resistance
Equivalent resistance 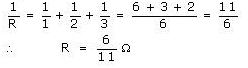
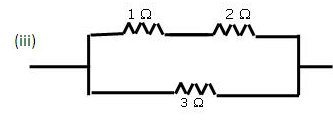 Equivalent resistance of first line = 1Ω + 2Ω = 3Ω Resistance of the second line = 3 0 Equivalent resistance
Equivalent resistance of first line = 1Ω + 2Ω = 3Ω Resistance of the second line = 3 0 Equivalent resistance
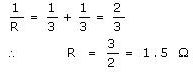
Page No:44
Question 47:
How will you connect three resistors of 2 Ω, 3 Ω and 5 Ω respectively so as to obtain a resultant resistance of
2.5 Ω ? Draw the diagram to show the arrangement.
Solution :
Given: Three resistances of 2ohms. 3ohms. 5ohms.
Their resultant. R = 2.5ohms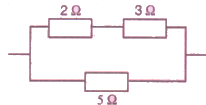
Resistance of first line = 2+3 = 5 ohm
So, 1/R = 1/5 + 1/5
On solving we get that
R = 2.5ohms
Question 48:
How will you connect three resistors of resistances 2 Ω, 3 Ω and 6Ω obtain a total n si stance of: (a) 4 Ω., and (b) 1Ω?
Solution :
(a) Connect 2ohms resistor in series with a parallel combination of 3ohms and 6ohms.
(b) Connect 2ohms. 3ohms. and 6ohms in parallel.
Question 49:
What is (a) highest, and (b) lowest, resistance which can be obtained by combining Com resistors having the following resistances ?
4 Ω, 8 Ω, 12 Ω, 24 Ω
Solution :
(a) For obtaining the highest resistance by combining the given resistances, we must connect them in series.
We get.
R = 4+8+12+24 = 48ohms
(b) For obtaining the lowest resistance by combining the given resistances, we must connect them in parallel.
We get.
1/R = 1/4+1/8+1/12+1/24
On solving we get. R = 2ohms
Question 50:
What is the resistance between A and B in the figure given below ?
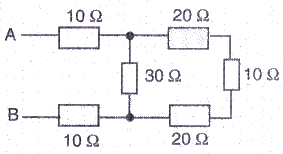
Solution :
The three resistance of 20 ohm. 10 ohm and 20 ohm on the extreme right side are in series.
So. the resultant of these three resistances = 20+20+10 = 50ohms.
This 50ohms is in parallel with 30ohms. So resultant of these two will be
1/R = 1/30+1/50
1/R = 80/1500
R = 18.75ohms
Now, the resistances 10 ohms. 18.75 ohms and 10 ohms are in series.
Therefore, resultant resistance = 18.75+10+10 = 38.75ohms.
Question 51:
You are given one hundred 1 Ω resister. What is the smallest and largest resistance you can make in a circuit using these ?
Solution :
Given: n=100. R=1 ohm
For obtaining the smallest resistance, these resistances are connected in parallel:
Equivalent resistance = 1/1 + 1/1 + 1/1 100 times = 100/1
Req = 1/100 = 0.01 ohm
For obtaining the largest resistance, these resistances are connected in series:
Equivalent resistance = 1 + 1 + 1 100 times = 100
Req = 100 ohm
Question 52:
You are supplied with a number of 100 Ω How could you combine some of these resisters to make a 250 Ω resistor ?
Solution : For obtaining 250ohms. connect two 100ohms in series with a parallel combination of two 100ohms.
Question 53:
The resistors R1, R2, R3 and R4 in the figure given below are all equal in value.
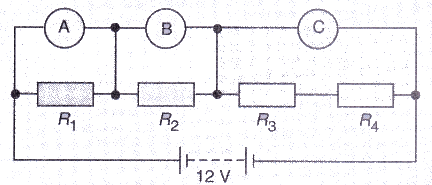
What would you expect the voltmeters A, B and C to read assuming that the connecting wires in the circuit have negligible resistance ?
Solution :
Req = R+R+R+R = 4R ohm
Total current in the circuit, I = V/R = 12/4R = 3/R
Reading of voltmeter A = Voltage across R1 = I x R1= 3/R x R = 3V
Reading of voltmeter B= Voltage across R2 = I X R2 = 3/R x R = 3V
Reading of voltmeter C= Voltage across the series combination of R3 and R4 = I X (R3+R4) = 3/R x 2R = 6V
Question 54:
Four resistances of 16 ohms each are connected in parallel. Four such combinations are connected in series.
What is the total resistance ?
Solution :
Resultant resistance of a parallel combination of four 16 ohm resistances is 1/R = 1/16 + 1/16 + 1/16 + 1/16 = 4/16
R = 4 ohm
Four such combinations are connected in series, so total resistance = 4+4+4+4 = 16 ohm.
Question 55:
If the lamps are both the same in the figure given below and if A1, reads 0.50 A, what do A2, A3, A4 and A5read ?
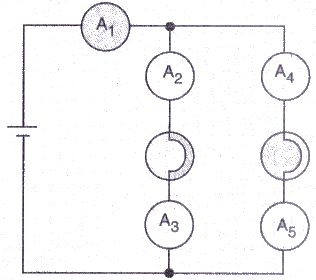
Solution : The total current of 0.5 A flowing in the circuit distributes equally in the two arms having lamps (since the lamps have same resistances). So the current through each of these arms is 0.25 A. Hence A2, A3, A4 and A5, all will read 0.25 A.
|
80 videos|569 docs|80 tests
|
FAQs on Lakhmir Singh & Manjit Kaur: Electricity, Solutions- 3 - Science Class 10
| 1. What is electricity? |  |
| 2. What is an electric circuit? |  |
| 3. What is the difference between AC and DC current? |  |
| 4. How is electricity generated? |  |
| 5. How can electricity be dangerous? |  |






















