JEE Advanced (Subjective Type Questions): Trigonometric Functions & Equations | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q. 1. If 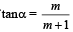 and
and 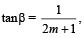 find the possible values of (α + β). (1978)
find the possible values of (α + β). (1978)
Ans. 
Sol. We know tan 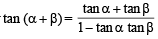
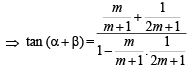
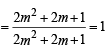

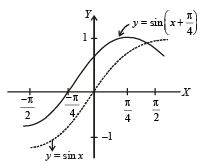
2. (a) Draw the graph of y =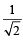 (sinx + cosx) from x =
(sinx + cosx) from x = 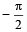 to
to 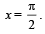
(b) If cos 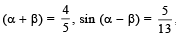 and α, β lies between 0 and
and α, β lies between 0 and 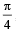 , find tan2α. (1979)
, find tan2α. (1979)
Ans.
Sol. (a) Given: 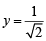 (sinx + cosx) sin
(sinx + cosx) sin 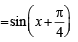 ...(1)
...(1)
Now, to draw the graph of 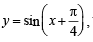 we first draw
we first draw
the graph of y = sin x and then on shifting it by 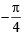 we will obtain the required graph as shown in figure given below.
we will obtain the required graph as shown in figure given below.
(b) 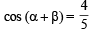
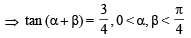

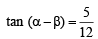
∴ tan 2α = tan [(α + β) + (α - β) ]
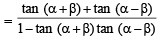
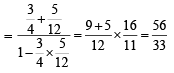
3. Given α + β - γ = π, prove that 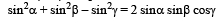 (1980)
(1980)
Ans.
Sol. Given α + β – γ = π and to prove that
sin2 α + sin2β – sin2γ = 2sinα sinβ cosγ
L.H.S. = sin2α + sin2β – sin2γ
[Using sin2α – sin2β = sin (A + B) sin (A – B)]
= sin2α + sin(β + γ) sin (β – γ)
= sin2α + sin(β + γ) sin (p – α) (∵ α + β – γ = π)
= sin2α + sin(β + γ) sinα
= sinα (sinα + sin(β + γ))
= sinα [sin [π – (β - γ)] + sin(β + γ)]
= sinα [sin(β - γ) + sin(β + γ)]
= sinα [2 sinβ cosγ] = 2 sinα sinβ cosγ = R.H.S.
4. Given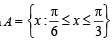 and f (x) = cos x – x (1 + x); find f (A). (1980)
and f (x) = cos x – x (1 + x); find f (A). (1980)
Ans.
Sol.
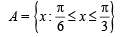
f (x) = cos x – x (1+ x)
f '(x) = – sin x – 1– 2x < 0, ∀ x∈A
∴ f is a decreasing function.
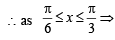
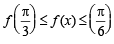
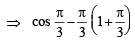
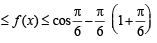
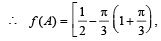
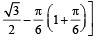
5. For all θ in [0, π/ 2] show that, cos (sinθ) ≥ sin (cos q) . (1981 - 4 Marks)
Ans. Sol. We have
cosθ + sinθ 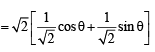
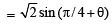
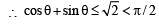
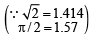
∴ cosθ + sinθ <π/ 2 ⇒ cosθ < π/ 2 - sinθ ...(1)
As q ∈ [0,π / 2] in which sinθ increases.
∴ Taking sin on both sides of eq. (1), we get
sin (cosθ ) < sin ( π /2 –sinθ )
sin (cosθ ) < cos (sinθ )
⇒ cos (sinθ ) > sin (cosθ ) ....(1)
Hence the result.
6. Without using tables, prove that
(sin 12°) (sin 48°) (sin 54°) = 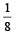 (1982 - 2 Marks)
(1982 - 2 Marks)
Ans. Sol. L.H.S. = sin 12° sin 48° sin 54° = 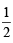 [2 sin 12° cos 42°] sin 54°
[2 sin 12° cos 42°] sin 54°
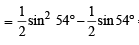
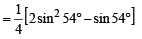
Now we know that sin 54°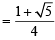
∴ We get, = 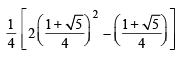
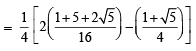
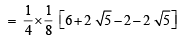
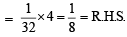
7. Show that 16cos 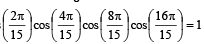 (1983 - 2 Marks)
(1983 - 2 Marks)
Ans. Sol. We know that,
cos A cos 2A cos 4A . . . . cos 2n
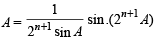
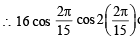
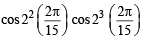
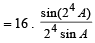 (where A = 2π/15)
(where A = 2π/15)
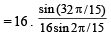
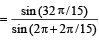
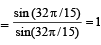
8. Find all the solution of 4 cos 2 x sin x - 2 sin2 x= 3 sinx (1983 - 2 Marks)
Ans. Sol. Given eq. is,
4 cos2 x sin x – 2 sin2 x = 3 sin x
⇒ 4 cos2 x sin x – 2 sin2 x – 3 sin x = 0
⇒ 4 (1 – sin2 x) sin x – 2 sin2 x – 3 sin x = 0
⇒ sin x [ 4 sin2 x + 2 sin x – 1] = 0
⇒ either sin x = 0 or 4 sin2 x + 2 sin x – 1 = 0
If sin x = 0 ⇒ x = np
⇒ If 4 sin2 x + 2 sin x – 1 = 0 ⇒ sin x = 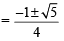
If sin x =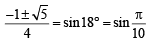
then 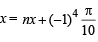
If sin x =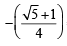 = sin(-540)
= sin(-540) 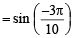
then x 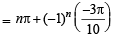
Hence, 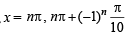
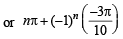
where n is some integer
9. Find the values of x∈(–π, +π) which satisfy the equation
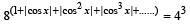 (1984 - 2 Marks)
(1984 - 2 Marks)
Ans. Sol. The given equation is
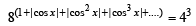
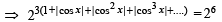
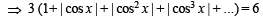
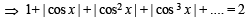
 NOTE THIS STEP
NOTE THIS STEP
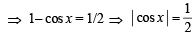
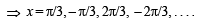
The values of 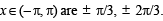
10. Prove that tanα + 2 tan 2α + 4 tan 4α + 8 cot 8α = cotα (1988 - 2 Marks)
Ans. Sol. We know that tan 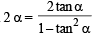
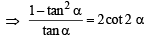 ⇒ cot α – tan α = 2 cot 2α
⇒ cot α – tan α = 2 cot 2α
Now we have to prove
tanα + 2 tan 2α + 4 tan 4α + 8 cot 8α = cot α
LHS
tan α + 2 tan 2α + 4 tan 4α + 4 (2 cot 2 . 4α)
= tan α + 2 tan 2α + 4 tan 4α + 4 (cot 4α - tan 4α) [Using (1)]
= tan α + 2 tan 2α + 4 tan 4α + 4 cot 4α - 4 tan 4α
= tan α + 2 tan 2α + 2 (2 cot 2. 2 a )
= tan α + 2 tan 2α + 2 (cot α – tan 2α)
= tan α + 2 tan 2α + 2 (2 cot 2α-tan 2α ) [Using (1)]
= tan α + 2 cot 2α
= tan α + (cot α-tan α) [Using (1)]
= cot α = RHS.
11. ABC is a triangle such that sin(2A + B) = sin (C – A) = – sin (B + 2C) = 
If A, B and C are in arithmetic progression, determine the values of A, B and C. (1990 - 5 Marks)
Ans. Sol. Given that in ΔABC, A, B and C are in A.P.
∴ A + C = 2B
also A + B + C = 180° ⇒ B + 2B = 180° ⇒ B = 60°
Also given that, sin (2A + B) = sin (C – A) = – sin (B + 2C) =
⇒ sin (2A + 60°) = sin (C – A) = – sin (60 + 2C) = 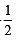 ..(1)
..(1)
From eq. (1), we have
sin (2A + 60°) = 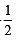 ⇒ 2A + 60° = 30° , 150°
⇒ 2A + 60° = 30° , 150°
but A can not be –ve
∴ 2A + 60° = 150° ⇒ 2A = 90 ° ⇒ A = 45°
Again from (1) sin (60° + 2C) = -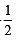
⇒ 60° + 2C = 210° or 330°
⇒ C = 75° or 135°
Also from (1) sin (C – A) =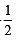 ⇒ C – A = 30°, 150°
⇒ C – A = 30°, 150°
For A = 45°, C =75° or 195° (not possible) ∴ C = 75°
Hence we have A = 45° , B = 60°, C = 75°
12. If exp {(sin2x + sin4x + sin6x + ............... ∞ ) In 2} satisfies the equation x2– 9x + 8 = 0, find the value of
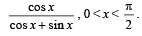 (1991 - 4 Marks)
(1991 - 4 Marks)
Ans. Sol. Let y = exp [sin2 x +sin4 x +sin6 x + . . . . ∞ ] ln 2
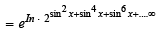
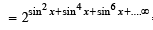
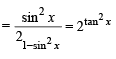
As y satisfies the eq.
x2 – 9x + 8 = 0 ∴ y2 – 9y + 8 = 0
⇒ (y – 1) (y – 8) = 0 ⇒ y = 1, 8
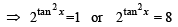
⇒ tan 2 x = 0 or tan 2x = 3
⇒ tan x = 0 or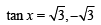
⇒ x = 0 or x = π/3, 2 π/3
But given that 0 < x < π/2 ⇒ x = π/3
Hence 
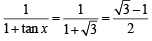
13. Show that the value of 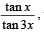 wherever defined never lies between
wherever defined never lies between 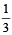 and 3. (1992 - 4 Marks)
and 3. (1992 - 4 Marks)
Ans.
Sol.
Let 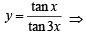
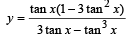
⇒ 3y – 3 tan2 x = 1– 3 tan2 x
⇒ (y – 3) tan2 x = 3y – 1 ⇒ 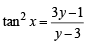
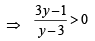 (L.H.S. being a prefect square)
(L.H.S. being a prefect square)
⇒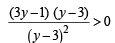 ⇒ (3y - 1) (y - 3)>0
⇒ (3y - 1) (y - 3)>0
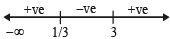
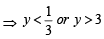
Thus y never lies between  and 3
and 3
14. Determine the smallest positive value of x (in degrees) for which tan(x + 100°) = tan (x + 50°) tan(x) tan (x – 50°). (1993 - 5 Marks)
Ans. Sol. Given that, tan (x + 100°) = tan (x + 50°) tan x tan (x – 50°)
⇒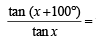 tan (x + 50°) tan (x – 50°)
tan (x + 50°) tan (x – 50°)
⇒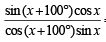
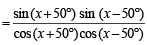
⇒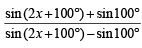
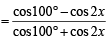
Applying componendo and dividendo, we get
⇒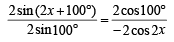
⇒ 2 sin (2x + 100°) cos 2x = – 2 sin 100° cos 100°
⇒ sin (4x + 100°) + sin 100° = – sin 200°
⇒ sin (4x + 10° + 90°) + sin (90° + 10°) = – sin (180 + 20°)
⇒ cos (4x + 10°) + cos 10° = sin 20°
⇒ cos (4x + 10°) = sin 20° – cos 10°
⇒ cos (4x + 10°) = sin 20° – sin 80°
= – 2 cos 50° sin 30° = – 2 cos 50°. 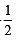 = –cos 50° = cos 130°
= –cos 50° = cos 130°
⇒ 4x + 10° = 130° ⇒ x = 30°
15. Find the smallest positive number p for which the equation cos(p sin x) = sin(p cos x) has a solution x ∈ [0,2π]. (1995 - 5 Marks)
Ans.
Sol. Given that cosθ = sin φ
where θ = p sin x, φ = p cos x
Above is possible when both 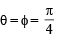 or
or 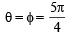
∴ p sin x =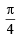 or p sin x =
or p sin x = 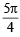
and p cos x = 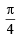 or p cos x =
or p cos x = 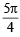
Squaring and adding, 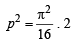
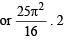
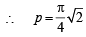 only for least positive value or
only for least positive value or 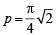
16. Find all values of θ in the interval 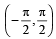 satisfying the equation
satisfying the equation  (1996 - 2 Marks)
(1996 - 2 Marks)
Ans.
Sol. Given :
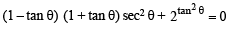
or 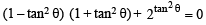
Let us put tan2 θ = t
∴ (1– t) ( 1 + t) + 2t = 0 or 1– t2 + 2t = 0
It is clearly satisfied by t = 3.
as – 8 + 8 = 0 ∴ tan2 θ = 3
∴ p = ± π/3 in the given interval.
17. Prove that the values of the function 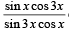 do not lie between
do not lie between 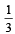 and 3 for any real x. (1997 - 5 Marks)
and 3 for any real x. (1997 - 5 Marks)
Ans.
Sol. Let 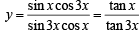
We have 
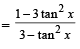
(the expression is not defined if tan x = 0)
⇒ 3y – (tan2 x) y = 1– 3 tan2 x ⇒ 3y – 1= (y – 3) tan2 x
⇒ 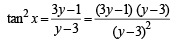
Since tan2 x > 0, we get (3y – 1) (y – 3) > 0
⇒ 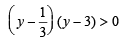
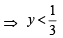 or y > 3
or y > 3
This shows that y cannot lie between  and 3.
and 3.
18. Prove that 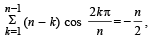 where n ≥ 3 is an integer. (1997 - 5 Marks)
where n ≥ 3 is an integer. (1997 - 5 Marks)
Ans.
Sol. Expanding the sigma on putting k = 1, 2, 3, ......, n
S = (n – 1) 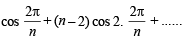
+ 1.cos (n – 1) 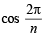 ... (1)
... (1)
We know that cosθ = cos (2π – θ)
Replacing each angle θ by 2π – θ in (1), we get
S = (n – 1) cos (n – 1) 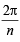 + (n – 2) cos (n – 2)
+ (n – 2) cos (n – 2) 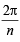 + ......+ 1.cos
+ ......+ 1.cos 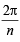 by (1) .....(2)
by (1) .....(2)
Add terms in (1) and (2) having the same angle and take n common
∴ 2S= 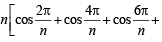
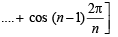
Angles are in A.P. of 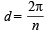
 NOTE THIS STEP
NOTE THIS STEP
= n .1 cosπ = – n ∵ sin (π – θ) = sinθ ∴ S = – n/2
19. In any triangle ABC, prove that (2000 - 3 Marks)
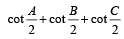
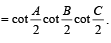
Ans. Sol. We have, A + B + C = π
⇒ 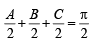
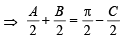
or 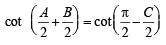
⇒ 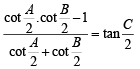
⇒ 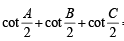
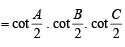
20. Find the range of values of t for which 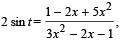
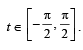
(2005 - 2 Marks)
Ans. Sol. Given that, 2 sin t 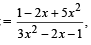 t ∈ [-π/ 2,π/ 2]
t ∈ [-π/ 2,π/ 2]
This can be written as
(6 sin t – 5) x2 + 2 (1– 2 sin t) x – (1+ 2 sin t) = 0
For given equation to hold, x should be some real number, therefore above equation should have real roots i.e., D ≥ 0
⇒ 4 (1– 2 sin t)2 + 4 (6 sin t – 5) (1+ 2 sin t) ≥ 0

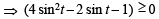
⇒ 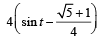

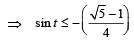
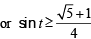
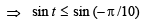 or
or 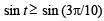
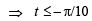 or
or 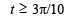
(Note that sin x is an increasing function from –π/2 to π/2)
∴ range of t is 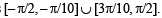
|
446 docs|930 tests
|

|
Explore Courses for JEE exam
|

|
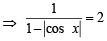 NOTE THIS STEP
NOTE THIS STEP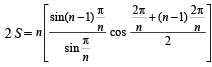 NOTE THIS STEP
NOTE THIS STEP
















