JEE Advanced (Subjective Type Questions): Quadratic Equation & Inequalities (Inequalities) | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. Solve for x : 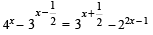          (1978)

Ans. 

Sol.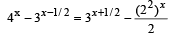  

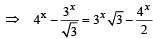
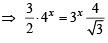
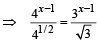
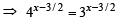
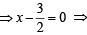 x = 3/2

Q.2. If (m , n) = 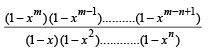 (1978)
 where m and n are positive integers (n ≤ m), show that (m, n + 1) = (m – 1, n + 1) + x^{m – n – 1} (m – 1, n).

Ans. 

Sol. RHS = (m – 1, n + 1) + x^{m – n –1} ( m - 1,n)

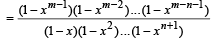
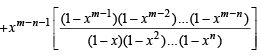
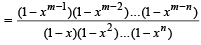
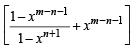
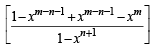
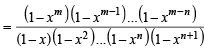
=  (m, n +1) = L.H.S. Hence Proved

Q.3. Solve for x :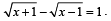 (1978)

Ans. 

Sol.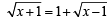 

Squaring both sides, we get

x +1 = 1+ x -1+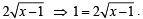 

⇒ 1 = 4 (x – 1)

⇒ x  = 5/4

Q.4. Solve the following equation for x : (1978)

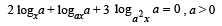
Ans. 

Sol.  Given a > 0, so we have to consider two cases :

a ≠ 1and a = 1.  Also it is clear that x > 0 and  x ≠ 1, ax ≠ 1, a²x ≠ 1.

Case I : If a > 0, ≠ 1

then given equation can be simplified as

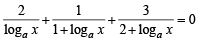
Putting log_a x = y, we get

2 (1 +  y) (2 + y) + y (2 + y) + 3y (1 + y) = 0

⇒ 6y² +11y + 4 = 0 ⇒y = -4/3 and-1/2

⇒ log_a x =-4 / 3 and log_ax =-1/2

⇒ x = a ^-4/3 and x=a^-1/2

Case II : If a = 1 then equation becomes

2 log_x1 + log_x1 + 3 log_x1 = 6 log_x1 = 0

which is true ∀ x > 0,≠1

Hence solution is  if  a = 1, x > 0, ≠ 1

if a > 0, ≠ 1 ; x= a^-1/2,a^-4/3

Q.5. Show that the square of 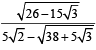  is a rational number.                      (1978)

Ans. Sol.  

Let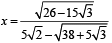 

⇒

⇒

⇒

⇒

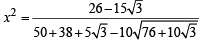
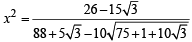
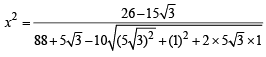
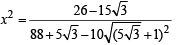
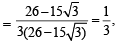which is a rational number..

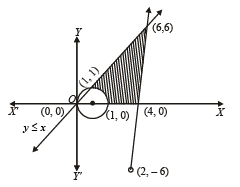
Q.6. Sketch the solution set of the followin g system of inequalities: x² + y² – 2x ≥ 0; 3x – y – 12 ≤ 0; y – x ≤ 0; y ≥ 0. (1978)

Ans. 

Sol.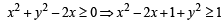 

⇒ (x – 1)² + y² ≥ 1 which represents the boundary and exterior region of the circle with centre at (1,0) and radius as 1.
For 3x – y ≤ 12, the corresponding equation is 3x – y = 12; any two points on it can be taken as (4, 0), (2, – 6). Also putting (0, 0) in given  inequation, we get 0 ≤ 12 which is true.

∴  given inequation represents that half plane region of line 3x – y = 12 which contains origin.
For y ≤ x, the corresponding equation y = x has any two points on it as (0, 0) and (1, 1). Also putting (2, 1) in the given i nequation, we get 1 ≤ 2 wh ich is true, so y ≤ x represents that half plane which contains the points (2, 1). y ≥ 0 represents upper half  cartesian plane.
Combining all we find the solution set as the shaded region in the graph.

Q.7. Find all integers x for which (1978)
 (5x – 1) < (x + 1)² < (7x – 3).

Ans. 

Sol. There are two parts of this question (5x – 1) < (x + 1)²  and  (x + 1)² <  (7x – 3)

Taking first part (5x -1) < (x +1)² ⇒ 5x -1 < x² + 2x+1

⇒ x² - 3x + 2 > 0 ⇒ (x-1)(x - 2)>0

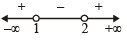       (using wavy method)

⇒ x < 1  or x > 2 ....(1)

Taking second part

(x +1)² < (7x -3) ⇒ x² - 5x +4< 0

⇒ ( x - 1)(x - 4)<0

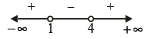         (using wavy method)

⇒ 1 <  x  < 4 ....(2)

Combining (1) and (2) [taking common solution], we get 2 < x < 4 but x is an integer therefore x = 3.

Q.8. If α, β are the roots of x² + px + q = 0 and γ, δ are the roots of x² + rx + s = 0, evaluate (α - γ) (α - δ) (β - γ) (β - δ) in terms of p, q, r and s.
 Deduce the condition that the equations have a common root.
 (1979)

Ans.

 Sol. ∵ α, β are the roots of x² + px + q = 0
∴  α + β = – p,     αβ = q
∵  γ,δ are  the roots of x² + rx + s = 0
∴ γ + δ=-r, γδ=s

Now, (α - γ)(α -δ)(β- γ)(β-δ

= [α² - (γ + δ)α + γδ][β² - (γ + δ)β + γδ]

= [α² + rα+ s][β² + rβ+s]

[∵ α , β are roots of x² + px + q = 0

∴ α² + pα + q = 0 and β² + pβ +q= 0]

= [(r - p)α + (s- q)][(r - p)β + ( s-q)]

= (r - p)² αβ + (r- p)( s -q)(α + β) + ( s-q)²

= q(r - p)² - p(r - p)(s -q) + (s-q)²

Now if the equations x²  +  px + q = 0 and x² + rx + s = 0 have a common root say α, then α² + pα + q = 0 and α² + rα + s = 0

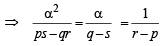
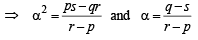
⇒ (q – s )2 = (r – p )(ps – qr) which is the required condition.

Q.9. Given n⁴ < 10ⁿ for a fixed positive integer n ≥ 2,  prove that (n + 1)⁴ < 10^{n + 1}. (1980)

Ans. 

Sol. Given that n⁴ < 10ⁿ for a fixed  + ve integer n ≥ 2.

To prove that (n + 1)⁴ < 10^{n + 1}

Proof : Since  n⁴ < 10ⁿ ⇒ 10n⁴ < 10^{n +1} ....(1)

So it is sufficient to prove that (n + 1)⁴ < 10n⁴

Now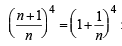 

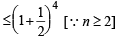
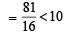
⇒ (n + 1)⁴ < 10n⁴ .... (2)

From  (1) and (2), (n +1)⁴ < 10^{n + 1}

Q.10. Let  y = 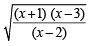         (1980)
 Find  all the real values of x for which y takes real values.

Ans. Sol. 

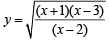
y will take all real values if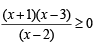  

By wavy method

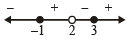
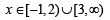
[2 is not included as it makes denominator zero, and hence y an undefined number.]

Q.11. For what values of m, does the system of equations
 3x + my = m
 2x – 5y = 20
 has solution satisfying the conditions x > 0, y > 0. (1980)

Ans. Sol.  The given equations are 3x + my – m = 0 and 2x – 5y – 20 = 0 Solving these equations by cross product method, we get

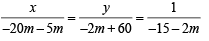 NOTE THIS STEP

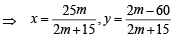
For 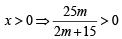  ....(1)

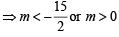
For 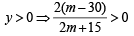 ....(2)

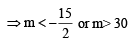
Combining (1) and (2), we get the common values of m as follows :

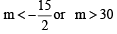
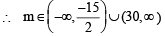
Q.12. Find the solution set of the system (1980)
 x + 2y + z = 1;
 2x – 3y – w = 2;

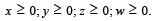
Ans. Sol. The given system is
x + 2y + z = 1 ....(1)
2x - 3y - ω =2 ....(2)
where  x, y, z, ω ≥ 0
Multiplying eqn. (1) by 2 and subtracting from (2), we get

7y + 2z + ω = 0 ⇒ ω = - (7 y+ 2z)

Now if y, z > 0, ω < 0 (not possible)

If  y = 0, z = 0 then x = 1 and ω = 0 .

∴ The only solution is x = 1, y = 0, z = 0, ω = 0 .

Q.13. Show that the equation e^{sin x} –e ^{– sinx} – 4 =0 has no real solution. (1982 - 2 Marks)

Ans.

Sol.  e^{sin x} - e^{- sinx} - 4=0

Let e^{sin x} = y then e ^{- sinx} = 1/y

∴ Equation becomes,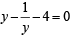

⇒ y² – 4y – 1 = 0  ⇒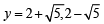

But y is real +ve number,

∴  

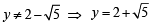
⇒ e^{sin x} = 2+ 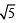  ⇒ sin x = log_e (2+)

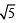But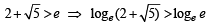

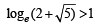⇒Hence, sin x > 1
Which is not possible.

∴ Given equation has no real solution.

Q.14. mn squares of euqal size are arranged to from a rectangle of dimension m by n,  where m and n are natural numbers.Two squares will be called ‘neighbours’ if they have exactly one common side. A natural number is written in each square such that the number written in any square is the arithmetic mean of the numbers written in its neighbouring squares.
 Show that this is  possible only if all the numbers used are equal. (1982 - 5 Marks)

Ans. Sol. For any square there can be at most 4, neighbouring squares.

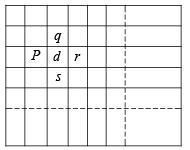
Let for a square having largest number d, p, q, r, s be written then

According to the question, p + q + r + s = 4d

⇒ (d – p) + (d – q) + (d – r) + (d – s) = 0

Sum of four +ve numbers can be zero only if these are zero individually

∴ d – p = 0 = d – q = d – r = d – s

⇒ p = q = r = s = d

⇒ all the numbers written are same.
Hence Proved.

Q.15. If one root of the quadratic equation ax² + bx + c = 0 is equal to the n-th power of the other, then show that

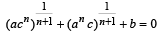 (1983 - 2 Marks)

Ans. Sol. 

Let α, β be the roots of eq. ax² + bx + c = 0

According to the question, β = aⁿ

Also α + β = – b/a  ; αβ = c/a

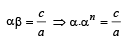
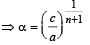
then α + β = – b/a ⇒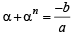 

or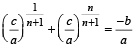 

⇒

⇒

⇒

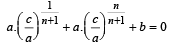
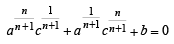
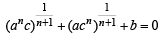
Hence Proved.

Q.16. Find all real values of x which satisfy x² - 3x + 2 > 0 and x² - 2 x - 4 ≤ 0 (1983 - 2 Marks)

Ans. Sol.  x² -3x+ 2 >0, x² -3x- 4 ≤ 0

⇒ (x – 1) (x – 2)  > 0 and (x – 4) (x + 1) < 0

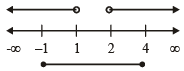
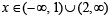  andx ∈ [-1, 4]

∴ Common solution is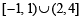 

Q.17. Solve for x; 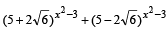   = 10  (1985 - 5 Marks)

Ans. Sol. The given equation is

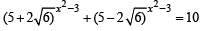....(1)

Let      ....(2)

then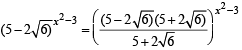  

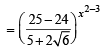
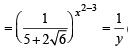(Using (2))

∴ The given equation (1) becomes 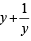  = 10

⇒ y² - 10y + 1=0 ⇒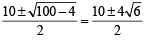 

⇒ y = 5 +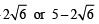

Consider, y = 5+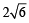 

⇒ 

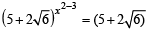
⇒ x² – 3 = 1 ⇒ x² = 4  ⇒ x = ± 2

Again consider

y = 5 -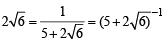 

⇒  ⇒ x² – 3 = – 1

⇒ x² = 2  ⇒ x  = ±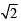

Hence the solutions are 2, – 2, , -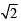

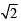
Q.18. For a ≤ 0, determine all r eal roots of the equation x² - 2a | x - a | - 3a² = 0 (1986 - 5 Marks)

Ans. 

Sol. The given equation is, x² – 2a | x – a | – 3a² = 0

Here two cases are possible.
Case I : x – a > 0 then | x – a | = x – a

∴ Eq. becomes x² – 2a (x – a) – 3a² = 0

or x² – 2ax – a² = 0 ⇒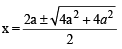 

⇒ x = a±a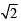

Case II : x – a < 0 then | x – a | = – (x – a)
∴ Eq. becomes
x² + 2a (x – a) – 3a² = 0

or x² + 2ax – 5a² = 0  ⇒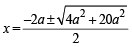 

  ⇒  ⇒

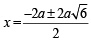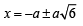
Thus the solution set is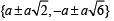 

Q.19. Find the set of all x for which 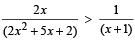 (1987 - 3 Marks)

Ans. Sol. We are given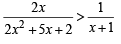 

⇒   

⇒ 

⇒ 

⇒ 

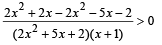
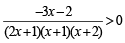
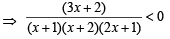
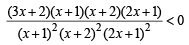
⇒ (3x + 2) (x + 1) (x + 2) (2x + 1) < 0 ....(1)
NOTE THIS STEP 

: Critical pts are x = – 2/3,  –1, – 2, – 1/2
On number line

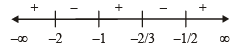
Clearly Inequality (1) holds for,

x ∈(– 2, – 1) ∪ (– 2/3, – 1/2)
[asx ≠ -2, -1, -2 / 3,-1 / 2]

Q.20. Solve | x² + 4 x + 3 | +2x + 5=0 (1988 - 5 Marks)

Ans. Sol.  The Given equation is, | x² + 4x + 3  | + 2x + 5 = 0 Now there can be two cases.

Case I : x² + 4x + 3≥0 ⇒ (x +1)(x + 3)≥0 ⇒ x ∈ (-∞, - 3] ∪ [-1,∞) ....(i)

Then given equation becomes,

⇒ x² + 6x + 8=0

⇒ ( x + 4)(x + 2)= 0 ⇒ x  = – 4, – 2

But x = – 2 does not satisfy (i), hence rejected

∴ x = – 4 is the sol.

Case II :   x² + 4x + 3 < 0

⇒ (x + 1) (x + 3) < 0

⇒ x ∈ (– 3, – 1) ....(ii)

Then given equation becomes, – (x² + 4x + 3) + 2x + 5 = 0

⇒ – x² – 2x + 2 = 0 ⇒ x² + 2x – 2 = 0

 ⇒ 

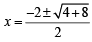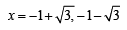
Out of which    x = – 1 – 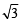  is sol.
Combining the two cases we get the solutions of given equation as      x = – 4, – 1–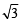

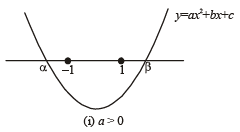
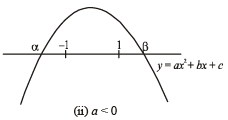
Q.21. Let a, b, c be real. If ax² + bx + c = 0 has two real roots α and β, where α < -1 and β > 1 , then show that

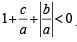 (1995 -  5 Marks)

Ans. Sol. Given that for a, b, c ∈ R, ax² + bx + c = 0 has two real roots a and b, where a < – 1 and b > 1. There may be two cases depending upon value of a, as shown below.
In each of cases (i) and (ii) af (–1) < 0 and af (1) < 0

⇒ a (a – b + c) < 0 and a (a + b + c) < 0 Dividing by a² (> 0), we get

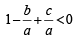       ....(1)

and  ....(2)

Combining (1) and (2) we get

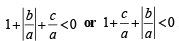Hence Proved.

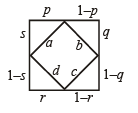
Q.22. Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a, b, c, and d denote the lengths of the sides of the quadrilateral, prove that 2 ≤ a²+b²+c²+d² ≤ 4. (1997 - 5 Marks)

 Ans. 

Sol. a² = p² + s², b² = (1– p)² + q²
c² = (1– q)² + (1 – r)²,  
d² = r² + (1– s)² 
∴ a2 + b² + c² + d² = {p² + (1– p)²}+{q² – (1– q)²}
+ { r² + (1– r)² } +{s² + (1– s)² }

where p, q, r, s all vary in the interval [0, 1].
Now consider the function

y² = x² + (1– x)², 0 ≤ x≤ 1,

⇒

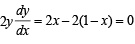
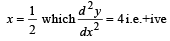
Hence y is minimum at x = 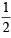 and its minimum

value is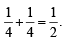 

Clearly value is maximum at the end pts which is 1.

∴ Minimum value of a² + b² + c² + d² =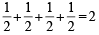 and maximum value is 1 + 1+ 1 + 1= 4. Hence proved.

Q.23. If α, β are the roots of ax² + bx + c = 0, ( a ≠ 0 ) and α + δ, β + δ are the roots of Ax² + Bx + C = 0,  ( A ≠ 0) for some constant δ, then prove that 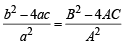 (2000 - 4 Marks)

Ans. Sol. We know that, (α-β)² = [(α+δ) - (β +δ)]²

⇒ (a+β)² - 4αβ = (α +δ+β+δ)² -4(α+δ)(β +δ)

⇒ 

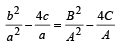
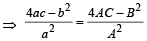
[Here α + β=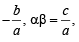

(α+δ) (β +δ)

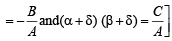
Hence proved.

Q.24. Let a, b, c be real numbers with a ≠ 0 and let α, β be the roots of the equation ax² + bx + c = 0. Express the roots of a3x² + abcx + c³ = 0 in terms of α, β. (2001 - 4 Marks)

Ans. Sol. Divide the equation by α³, we get

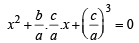
⇒ x² – (α + β). (αβ) x + (αβ)³ = 0
⇒ x² – α²βx – αβ² x  + (αβ)³ = 0
⇒ x (x – α²β) – αβ² (x – α²β) = 0
⇒ (x – α²β) (x – αβ²) = 0
⇒ x = α² β, αβ²
which is the required answer.

Q.25. If x² + (a – b) x + (1 – a – b) = 0 where a, b ∈ R then find the values of a for which equation has unequal real roots for all values of b. (2003 - 4 Marks)

Ans. Sol. The given equation is, x² + (a – b) x + (1– a – b) = 0, a, b ∈ R
For this eqn to have unequal real roots ∀ b D > 0
⇒ (a – b)² – 4 (1– a – b) > 0
⇒ a² + b² – 2ab – 4 + 4a + 4b > 0
⇒ b²  + b (4 – 2a) + a² + 4a – 4 > 0
Which is a quadratic expression in b, and it will be true ∀ b∈R if discriminant of above eqn less than zero.

i.e., ( 4 –2a)²  – 4 (a² + 4a – 4) < 0
⇒ (2 – a)² – (a² + 4a – 4) < 0
⇒  4 – 4a + a² – a² – 4a + a < 0
⇒  – 8a + 8 <  0
⇒ a > 1

Q.26. If a, b, c are positive real numbers. Then prove that (a + 1)⁷ (b + 1)⁷ (c + 1)⁷>7⁷ a⁴b⁴c⁴ (2004 - 4 Marks)

Ans. Sol. Given that a, b, c are positive real numbers. To prove that (a + 1)⁷ (b + 1)⁷ (c + 1)⁷  > 7 ⁷ a⁴b⁴c⁴ 
Consider L.H.S. = (1+ a)⁷. (1+ b)⁷. (1+ c)⁷                        
=  [(1 + a) (1+ b) (1+ c)]⁷[1 + a + b + c + ab + bc + ca + abc]⁷ 
> [a + b + c + ab + bc + ca + abc]7 ....(1)
Now we know that AM ≥ GM using it for +ve no’s a, b, c, ab, bc, ca and abc, we get

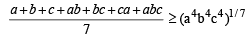
 ⇒ (a + b + c + ab + bc + ca+ abc)⁷ ≥ 7⁷ (a⁴b⁴c⁴)a
From (1) and (2),
we get [(1 + a) (1 + b) ( 1 + c)]⁷  > 7⁷a⁴ b⁴ c⁴
Hence Proved.

Q.27. Let a and b be the roots of the equation x² – 10cx – 11d = 0 and those of x² – 10ax – 11b = 0 are c, d then the value of a + b + c + d, when a ≠ b ≠ c ≠ d, is. (2006 - 6M)

Ans. Sol. Roots of   x² – 10cx – 11d = 0 are a and b ⇒ a + b = 10c and ab = – 11d
Similarly c and d are the roots of x² – 10ax – 11b = 0
⇒ c + d = 10a and cd = – 11b
⇒ a + b + c + d = 10 (a + c) and abcd = 121 bd
⇒ b + d = 9(a + c) and ac = 121
Also we have a² – 10 ac – 11d = 0 and c² – 10ac – 11b = 0
⇒ a² + c² – 20ac – 11 (b + d) = 0
⇒ (a + c)² – 22 × 121 – 99 (a + c) = 0
⇒ a + c = 121 or – 22 For a + c = – 22,
we get a = c
∴ rejecting this value we have a + c = 121
∴ a + b + c + d =10 (a + c) = 1210