JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The larger of 9950 + 10050 and 10150 is ................ (1982 - 2 Marks)
Ans. (101)50
Sol. Consider (101)50 – {(99)50 + (100)50} = (100 + 1)50 – (100 – 1)50 – (100)50
= (100)50 [(1+ 0.0 1)50 – (1– 0.01)50 – 1]
= (100)50 [2 (50C1(0.01) + 50C3(0.01)3 + ....) – 1]
= (100)50 [2 (50C3(0.01)3 + ....)] > 0
∴ (101)50 > (99)50 + (100)50
∴ (101)50 is greater.
Q.2. The sum of the coefficients of the plynomial (1 + x – 3x2)2163 is ................ (1982 - 2 Marks)
Ans. -1
Sol. If we put x = 1 in the expansion of (1+ x – 3x2)2163 = A0 + A1x + A2x2 + ...
we will get the sum of coefficients of given polynomial, which clearly comes to be – 1.
Q.3. If (1 + ax )n = 1 + 8x + 24x2 + .... then a = ...... and n = ............... (1983 - 2 Marks)
Ans. a = 2, n = 4
Sol. (1 + ax)n = 1 + 8x + 24x2 + ...
⇒ (1 + ax)n = 1 + nxa +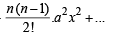
= 1 + 8 x + 24x 2+ ...
Comparing like powers of x we get
nax = 8x ⇒ na = 8 ....(1)

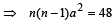 ....(2)
....(2)
Solving (1) and (2), n = 4, a = 2
Q.4. Let n be positive integer. If the coefficients of 2nd, 3rd, and 4th terms in the expansion of (1 + x)n are in A.P., then the value of n is .............. (1994 - 2 Marks)
Ans. 7
Sol. We know that for a +ve integer n (1 + x)n = nC0 + nC1 x + nC2 x2 + ......+ nCn xn
ATQ coefficients of 2nd, 3nd, and 4th terms are in A.P. i.e.nC1, nC2, nC3 are in A.P.
⇒ 2.nC2 = nC1 + nC3
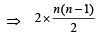
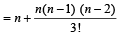
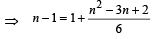 ⇒ n2 – 9n + 14 = 0
⇒ n2 – 9n + 14 = 0
⇒ (n – 7) (n – 2) = 0 ⇒ n = 7 or 2
But for the existance of 4th term, n = 7.
Q.5. The sum of the rational terms in th e expansion of 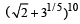 is ................ (1997 - 2 Marks)
is ................ (1997 - 2 Marks)
Ans. 41
Sol. Let Tr +1 be the general term in the expansion of
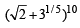
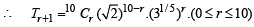
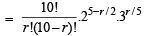
Let Tr +1will be rational if 25–r/2 and 3r/5 are rational numbers.
⇒ 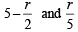 are integers.
are integers.
⇒ r = 0 and r = 10 ⇒ T1 and T11 are rational terms.
⇒ Sum of T1 and T11 = 10C025 – 0.30 + 10C1025–5.32
= 1.32.1 + 1.1.9 = 32 + 9 = 41
|
446 docs|929 tests
|





















