Integer Answer Type Questions: Sequences and Series | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. Let Sk, k = 1, 2, ….. , 100, denote the sum of the infinite geometric series whose first term is
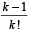 and the common ratio is
and the common ratio is 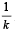 . Then the value of
. Then the value of
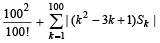 is (2010)
is (2010)
Ans. (3)
Sol. Using  we get
we get
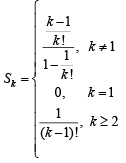
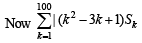
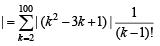
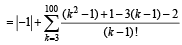
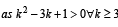

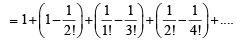
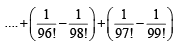
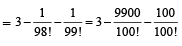
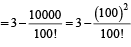
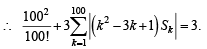
Q.2. Let a1,a2,a3........, a11 be real numbers satisfying
a1=15, 27–2a2> 0 and ak=2ak–1–ak–2 for k = 3, 4,..........11.
if  , then the value of
, then the value of
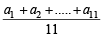 is equal to (2010)
is equal to (2010)
Ans. (0)
Sol. Given that ak = 2ak –1–ak –2
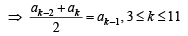
⇒ a1 , a2 , a3 , ...,a11 are in AP..
If a is the first term and D the commen difference then
a21 + a22 + ... +a211= 990 (
⇒ 11a 2 + d 2 (12 + 22 + ...+ 102 ) + 2ad (1 + 2 + ...+ 10) = 990
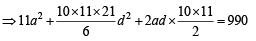
⇒ a2 + 35d2 + 150d= 90 Using a = 15,
we get 35d2 + 150d +135 = 0 or 7d2 + 30d + 27= 0
⇒ d +3)(7d +9) = 0 ⇒ d= –3 or – 9/7
then a2 = 15 - 3 = 12 or 15
∴ d ≠ – 97
Hence 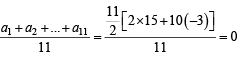
Q.3. Let a1, a2, a3 .....a100 be an arithmetic progression with a1 = 3 and 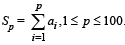 For any integer n with 1 ≤ n ≤ 20 , let m = 5n. If
For any integer n with 1 ≤ n ≤ 20 , let m = 5n. If 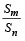 does not depend on n, then a2 is (2011)
does not depend on n, then a2 is (2011)
Ans. (9)
Sol. We have 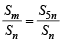
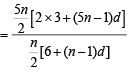
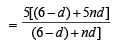
which will be independent of n if d = 6 or d = 0 For a proper A.P. we take d = 6 then a2 = 3 + 6 = 9
Q.4. A pack con tain s n cards n umber ed fr om 1 to n . Two consecutive numbered cards are removed from the pack and the sum of the numbers on the remaining cards is 1224. If the smaller of the numbers on the removed cards is k, then k – 20 = (JEE Adv. 2013)
Ans. (5)
Sol. Let k, k + 1 be removed from pack.
∴ (1 + 2 + 3 + ... + n) – (k + k + 1) = 1224

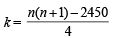
for n = 50, k = 25 ∴ k – 20 = 5
Q.5. Let a, b, c be positive integers such that 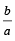 is an integer. If a,b, c are in geometric progression and the arithmetic mean of a, b, c is b + 2, then the value of
is an integer. If a,b, c are in geometric progression and the arithmetic mean of a, b, c is b + 2, then the value of 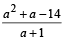 is
is
(JEE Adv. 2014)
Ans. (4)
Sol. ∵ a, b, c are in G.P
∴ b = ar and c = ar2
Also 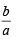 is an integer
is an integer
⇒ r is an integer
∵ A.M. of a, b, c is b + 2
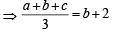
⇒ a + ar + ar2 = 3ar+6
⇒ a (r2 - 2r + 1)=6
⇒ a (r - 1)2=6 .
∵ a and r are integers
∴ The only possible values of a and r can be 6 and 2 respectively.
Then 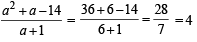
Q.6. Suppose that all the terms of an arithmetic progression (A.P.) are natural numbers. If the ratio of the sum of the first seven terms to the sum of the first eleven terms is 6 : 11 and the seventh term lies in between 130 and 140, then the common difference of this A.P. is (JEE Adv. 2015)
Ans. (9)
Sol.
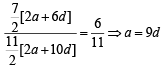
a7 = a + 6d = 15d
∵ 130 < 15d < 140 ⇒ d = 9
(∵ All terms are natural numbers ∴ d ∈N )
Q.7. The coefficient of x9 in the expansion of (1 + x) (1 + x2) (1 + x3) ... (1 + x100) is (JEE Adv. 2015)
Ans. (8)
Sol. In expansion of (1 + x) (1 + x2) (1 + x3) .... (1 + x100) x9 can be found in the following ways x9, x1 +2 8, x 2 + 7, x3 + 6, x4 + 5, x1 + 2 + 6, x1 + 3 + 5, x2 + 3 + 4 The coefficient of x9 in each of the above 8 cases is 1. ∴ Required coefficient = 8.
|
347 docs|185 tests
|
FAQs on Integer Answer Type Questions: Sequences and Series - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is a sequence in mathematics? |  |
| 2. What is the difference between a sequence and a series? |  |
| 3. What is an arithmetic sequence? |  |
| 4. How do you find the nth term of an arithmetic sequence? |  |
| 5. What is a geometric sequence? |  |





















