JEE Advanced (Matrix Match): Conic Sections | Chapter-wise Tests for JEE Main & Advanced PDF Download

DIRECTIONS : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :

If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

Q.1. Match the following : (3, 0) is the pt. from which three normals are drawn to the parabola y² = 4x which meet the parabola in the points P, Q and R. Then (2006 - 6M)

Ans. (A)-(p), (B)-(q), (C)-(s), (D)-(r) 

Sol.  Let y = mx – 2m – m³ be the equation of normal to y² = 4x.
As it passes through (3, 0), we get m = 0, 1, – 1
Then three points on parabola are given by (m², – 2m) for m = 0, 1, – 1
∴ P (0, 0), Q (1, 2), R (1, – 2)

∴ Area of ΔPQR = 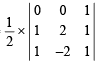  = 2 sq. units

Radius of circum-circle,

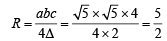      NOTE THIS STEP
(where, a, b, c are the sides of ΔPQR)

Centroid of ΔPQR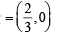

Circumcentre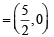

Thus, (A) - (p); (B) - (q); (C) – (s); (D) – (r)

DIRECTIONS : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :

If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

2. Match the statements in Column I with the properties in Column II and indicate your answer by darkening the appropriate bubbles in the 4 × 4 matrix given in the ORS. (2007 -6 marks)

Ans. (A)-p, q; (B)-p, q ; (C)-q, r ; (D)-q, r

Sol. (A) - p, q

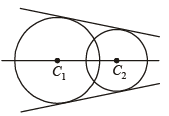
It is clear from the figure that two intersecting circles have a common tangent and a common normal joining the centres (B) - p, q

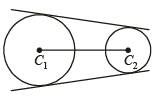
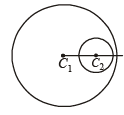
(C) – q, r Two circle when one is completely inside the other have a common normal C₁C₂ but no common tangent.

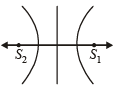
(D) – q, r Two branches of hyperbola have no common tangent but have a common normal joining S₁S₂

Matrix Match (A) – p, q; (B) – p, q; (C) – q, r; (D) – q, r

DIRECTIONS : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :

If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

3. Match the conics in Column I with the statements/expressions in Column II. (2009)

Ans. (A)-p; (B)-s, t ; (C)-r ; (D)-q, s

Sol. (p) As the line hx + ky= 1, touches the circle x² +y²= 4
∴ Length of perpendicular from centre (0 , 0) of circle to line = radius of the circle

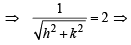
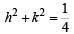
∴ Locus of (h, k) is 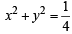  , which is a circle.

(q) We know that if | z -z₁ | - | z -z₂|= k
where | k | < | z₁-z₂| then z traces a hyperbola.
Here | z + 2 | - |z - 2 | =±3
∴ Locus of z is a hyperbola.

(r) We have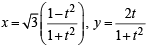

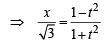and  

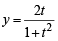
On squaring and adding, we get

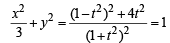 or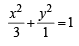  

which is the equation of an ellipse.

(s) We know eccentricity for a parabola = 1
for an ellipse < 1
for a hyperbola > 1
∴ The conics whose eccentricity lies in 1 ≤ x <∞ are parabola and hyperbola.

(t) Let z = x+ iy then
Re [( x + 1) + iy]² = x²+y²+1
⇒ (x + 1)² - y² = x² +y²+1 ⇒ y² =x , which is a parabola.

DIRECTIONS (Q. 4) : Following question has matching lists. The codes for the list have choices (a), (b), (c) and (d) out of which ONLY ONE is correct.

Q. 4. A line L : y = mx + 3 meets y – axis at E(0, 3) and the arc of the parabola y² = 16x, 0 ≤ y ≤ 6 at the point F(x₀, y₀). The tangent to the parabola at F(x₀, y₀) intersects the y-axis at G(0, y₁). The slope m of the line L is chosen such that the area of the triangle EFG has a local maximum.     (JEE Adv. 2013) Match List I with List II and select the correct answer using the code given below the lists :

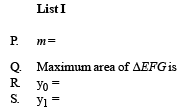
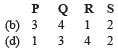
Ans. (a)

Sol. (a) Equation of tangent to y² = 16x at F (x₀, y₀) yy₀ = 8(x + x₀)

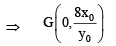
Area of ΔEFG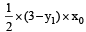

⇒

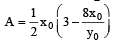
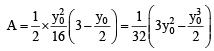
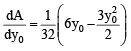
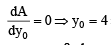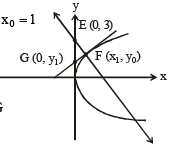
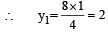
Also y₀ = mx₀ + 3
∴  4 = m + 3  or m = 1 maximum area of ΔEFG

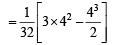
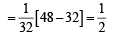
∴ (P) → (4), (Q) → (1), (R) → (2), (S) → (3)