Ex-19.5, Geometrical Constructions, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
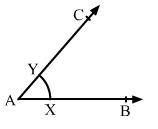
Q.1 Draw an angle and label it as ∠BAC. Construct another angle, equal to ∠BAC
Sol.1 : Draw an angle ∠BAC also draw a ray OP.
With a suitable radius and A as center, draw an arc intersecting AB and AC at X and Y, respectively.
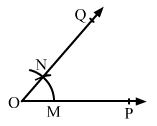
With the same radius and O as center, draw an arc to intersect the arc OP at M.
Measure XY using the compass.
With M as centre and radius equal to XY, draw an arc to intersect the arc drawn from O at N.
Join 0 and N and extend it to Q.
∠POQ is the required angle.
Q.2 Draw an obtuse angle. Bisect it. Measure each of the angle obtained.
Sol.2 : Obtuse angles are those angles which are greater than 90° but less than 180°.
Draw an obtuse angle ∠BAC.
With an appropriate radius and centre at A, draw an arc such that it intersects AB and AC at P and Q, respectively.
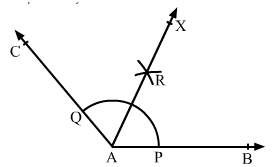
With centre P and radius more than half of PQ, draw an arc.
With the same radius and centre at Q, draw another arc intersecting the previous arc at R.
Join A and R and extend it to X.
The ray AX is the required bisector of ∠BAC.
If we measure ∠BAR and ∠CAR,
we have ∠BAR = ∠CAR = 65°
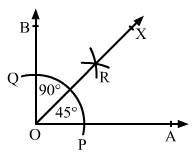
Q.3 Using protractor, draw an angle of measure 1080. With this angle as given,draw an angle of 540.
Sol.3 : Draw a ray OA.
With the help of a protractor, construct an angle ∠AOB of 108°.
Since, 108/2 = 540
Therefore, 54° is half of 108°.
To get the angle of 54°, we need to bisect the angle of 108°.
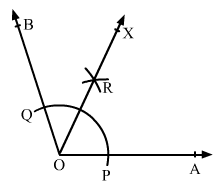
With centre at O and a convenient radius, draw an arc cutting sides OA and OB at P and Q, respectively.
With centre at P and radius more than half of PQ, draw an arc.
With the same radius and centre at Q, draw another arc intersecting the previous arc at R.
Join O and R and extend it to X.
∠AOX is the required angle of 54°.
Q.4 Using protractor, draw a right angle. Bisect it to get an angle of measure 450.
Sol.4 : We know that a right angle is of 90°.
Draw a ray OA.
With the help of a protractor, draw an ∠AOB of 90°.
With centre at O and a convenient radius, draw an arc cutting sides OA and OB at P and Q, respectively.
With centre at P and radius more than half of PQ, draw an arc.
With the same radius and centre at Q, draw another arc intersecting the previous arc at R.
Join O and R and extend it to X.
∠AOX is the required angle of 45°.
∠AOB = 90°
∠AOX = 45°
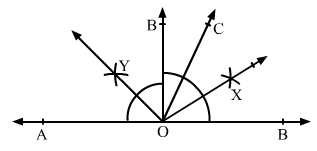
Q.5 Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Sol.5 : Two angles, which are adjacent and supplementary, are called linear pair of angles.
Draw a line AB and mark a point O on it.
When we draw any angle ∠AOC, we also get another angle ∠BOC.
Bisect ∠AOC by a compass and a ruler and get the ray OX.
Similarly, bisect ∠BOC and get the ray OY.
Now,
∠XOY = ∠XOC + ∠COY
= 1/2 ∠AOC + 12 ∠BOC
= 1/2(∠AOC + ∠BOC)
= 1/2 x 180° = 90° (As ∠AOC and ∠BOC are supplementary angles)
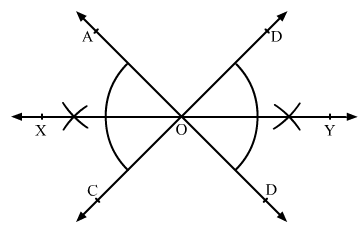
Q.6 Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line.
Sol.6 : Draw two lines AB and CD intersecting each other at O.
We know that the vertically opposite angles are equal.
Therefore, ∠BOC = ∠AOD and
∠AOC = ∠BOD.
We bisect angle AOC and draw the bisecting ray as OX.
Similarly, we bisect angle BOD and draw the bisecting ray as OY.
Now, ∠XOA + ∠AOD + ∠DOY
= 1/2 ∠AOC + ∠AOD + 1/2 ∠BOD
= 1/2 ∠BOD + ∠AOD + 1/2 ∠BOD
[As, ∠AOC = ∠BOD]
= ∠AOD + ∠BOD
Since, AB is a line.
Therefore, ∠AOD and ∠BOD are supplementary angles and the sum of these two angles will be 180°.
Therefore, ∠XOA + ∠AOD + ∠DOY = 180°
We know that the angles on one side of a straight line will always add to 180°.
Also, the sum of the angles is 180°.
Therefore, XY is a straight line.
Thus, OX and OY are in the same line.
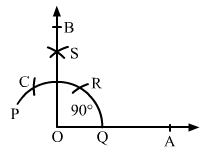
Q.7 Using ruler and compass only, draw a right angle.
Sol.7 : Draw a ray OA.
With a convenient radius and centre at O, draw an arc PQ with the help of a compass intersecting the ray OA at P.
With the same radius and centre at P, draw another arc intersecting the arc PQ at R.
With the same radius and centre at R, draw an arc cutting the arc PQ at C, opposite P.
Taking C and R as the centre, draw two arcs of radius more than half of CR that intersect each other at S.
Join O and S and extend the line to B.
∠AOB is the required angle of 900.
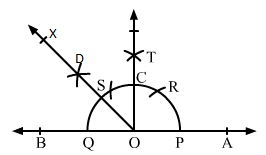
Q.8 Using ruler and compass only, draw an angle of measure 1350.
Sol.8 : We draw a line AB and mark a point O on it.
With a convenient radius and centre at O, draw an arc PQ with the help of a compass intersecting the line AB at P and Q.
With the same radius and centre at P, draw another arc intersecting the arc PQ at R.
With the same radius and centre at Q, draw one more arc intersecting the arc PQ at S, opposite to P.
Taking S and R as centres and radius more than half of SR, draw two arcs intersecting each other at T.
Join O and T intersecting the arc PQ at C.
Taking C and Q as centres and radius more than half of CQ, draw two arcs intersecting each other at D.
Join O and D and extend it to X to form the ray OX.
∠AOX is the required angle of measure 135°.
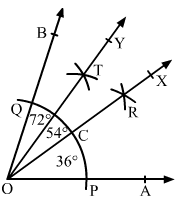
Q.9 Using a protractor, draw an angle of measure 720. With this angle as given, draw angles of measure 360 and 540.
Sol.9 : Draw a ray OA.
With the help of a protractor, draw an angle ∠AOB of 72°.
With a convenient radius and centre at O, draw an arc cutting sides OA and OB at P and Q, respectively.
With P and Q as centres and radius more than half of PQ, draw two arcs cutting each other at R.
Join O and R and extend it to X.
OR intersects arc PQ at C.
With C and Q as centres and radius more than half of CQ, draw two arcs cutting each other at T.
Join O and T and extend it to Y.
Now, OX bisects ∠AOB
Therefore, ∠AOX = ∠BOX = 72/2=36°
Again, OY bisects ∠BOX
Therefore, ∠XOY = ∠BOY = 36/2 = 18°
Therefore, ∠AOX is the required angle of 36° and ∠AOY = ∠AOX + ∠XOY = 36° + 18° = 54°
Therefore, ∠AOY is the required angle of 54°.
FAQs on Ex-19.5, Geometrical Constructions, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What are geometrical constructions in mathematics? |  |
| 2. How do you construct an equilateral triangle using a compass and straightedge? |  |
| 3. How do you construct a perpendicular bisector of a line segment? |  |
| 4. How can you construct a line parallel to another line through a given point? |  |
| 5. How do you construct a square using a compass and straightedge? |  |
















