Ex-23.4, Data Handling II Central Values, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Find the mode and median of the data: 13, 16, 12, 14, 19, 12, 14, 13, 14
By using the empirical relation also find the mean.
Answer 1:
Arranging the data in ascending order such that same numbers are put together, we get:
12,12,13,13, 14,14,14, 16, 19
Here, n = 9.
∴ Median = Value of 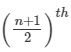 observation = Value of the 5th observation = 14.
observation = Value of the 5th observation = 14.
Here, 14 occurs the maximum number of times, i.e., three times. Therefore, 14 is the mode of the data.
Now,
Mode = 3 Median - 2 Mean
⇒ 14 = 3 x 14 - 2 Mean
⇒2 Mean = 42 - 14 = 28
⇒ Mean = 28 ÷ 2 = 14.
Question 2:
Find the median and mode of the data: 35, 32, 35, 42, 38, 32, 34
Answer 2:
Arranging the data in ascending order such that same numbers are put together, we get:
32, 32, 34,35,35, 38,42.
Here, n = 7
∴ Median = Value of 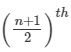 observation = Value of the 4th observation = 35.
observation = Value of the 4th observation = 35.
Here, 32 and 35, both occur twice. Therefore, 32 and 35 are the two modes.
Question 3:
Find the mode of the data: 2, 6, 5, 3, 0, 3, 4, 3, 2, 4, 5, 2, 4
Answer 3:
Arranging the data in ascending order such that same values are put together, we get:
0, 2, 2, 2, 3, 3,3,4,4,4,5,5,6.
Here, 2,3 and 4 occur three times each. Therefore, 2 ,3 and 4 are the three modes.
Alternate Solution
Arranging the data in the form of a frequency table, we have:
| Values | Tally Bars | Frequency |
| 0 | ∣ | 1 |
| 2 | ∣∣∣ | 3 |
| 3 | ∣∣∣ | 3 |
| 4 | ∣∣∣ | 3 |
| 5 | ∣∣ | 2 |
| 6 | ∣ | 1 |
| Total | 13 |
Clearly, the values 2,3 and 4 occur the maximum number of times, i.e., three times.
Hence, the mode is 2,3 and 4.
Question 4:
The runs scored in a cricket match by 11 players are as follows:
6, 15, 120, 50, 100, 80, 10, 15, 8, 10, 10
Find the mean, mode and median of this data.
Answer 4:
Arranging the data in ascending order such that same values are put together, we get:
6,8,10,10,10,15,15,50,80,100,120.
Here, n = 11
∴ Median = Value of 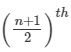 observation = Value of the 6th observation = 15.
observation = Value of the 6th observation = 15.
Here, 10 occurs three times. Therefore, 10 is the mode of the given data.
Now,
Mode = 3 Median - 2 Mean
⇒ 10 = 3 x 15 - 2 Mean
⇒2 Mean = 45 - 10 = 35
⇒ Mean = 35 ÷ 2 = 17.5.
Question 5:
Find the mode of the following data:
12, 14, 16, 12, 14, 14, 16, 14, 10, 14, 18, 14
Answer 5:
Arranging the data in ascending order such that same values are put together, we get:
10,12,12,14,14,14,14,14,14, 16, 16, 18.
Here, clearly, 14 occurs the most number of times.
Therefore, 14 is the mode of the given data.
Alternate solution:
Arranging the data in the form of a frequency table, we get:
| Values | Tally Bars | Frequency |
| 10 | ∣ | 1 |
| 12 | ∣∣ | 2 |
| 14 | 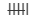 | 6 |
| 16 | ∣∣ | 2 |
| 18 | ∣ | 1 |
| Total | 12 |
Clearly, 14 has maximum frequency. So, the mode of the given data is 14.
Question 6:
Heights of 25 children (in cm) in a school are as given below:
168, 165, 163, 160, 163, 161, 162, 164, 163, 162, 164, 163, 160, 163, 163, 165, 163, 162, 163, 164, 163, 160, 165, 163, 162
What is the mode of heights?
Also, find the mean and median.
Answer 6:
Arranging the data in tabular form, we get:
| Height of Children (cm) | Tally Bars | Frequency |
| 160 | ∣∣∣ | 3 |
| 161 | ∣ | 1 |
| 162 | ∣∣∣∣ | 4 |
| 163 | 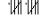 | 10 |
| 164 | ∣∣∣ | 3 |
| 165 | ∣∣∣ | 3 |
| 168 | ∣ | 1 |
| Total | 25 |
Here, n = 25
∴ Median = Value of 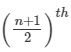 observation = Value of the 13th observation = 163 cm.
observation = Value of the 13th observation = 163 cm.
Here, clearly, 163 cm occurs the most number of times. Therefore, the mode of the given data is 163 cm.
Now,
Mode = 3 Median - 2 Mean
⇒ 163 = 3 x 163 - 2 Mean
⇒2 Mean = 326
⇒ Mean = 326 ÷ 2 = 163 cm.
Question 7:
The scores in mathematics test (out of 25) of 15 students are as follows:
19, 25, 23, 20, 9, 20, 15, 10, 5, 16, 25, 20, 24, 12, 20
Find the mode and median of this data. Are they same?
Answer 7:
Arranging the data in ascending order such that same values are put together, we get:
5,9,10,12,15,16, 19, 20, 20, 20, 20, 23, 24, 25, 25.
Here, n = 15
∴ Median = Value of 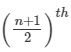 observation = Value of the 8th observation = 20.
observation = Value of the 8th observation = 20.
Here, clearly, 20 occurs the most number of times, i.e., 4 times. Therefore, the mode of the given data is 20.
Yes, the median and mode of the given data are the same.
Question 8:
Calculate the mean and median for the folllowing data:
| Marks | : | 10 | 11 | 12 | 13 | 14 | 16 | 19 | 20 |
| Number of students | : | 3 | 5 | 4 | 5 | 2 | 3 | 2 | 1 |
Using empirical formula, find its mode.
Answer 8:
Calculation of Mean
| Marks (xi) | 10 | 11 | 12 | 13 | 14 | 16 | 19 | 20 | Total |
| Number of Students (fi) | 3 | 5 | 4 | 5 | 2 | 3 | 2 | 1 | 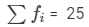 |
| fixi | 30 | 55 | 48 | 65 | 28 | 48 | 38 | 20 | 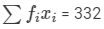 |
Mean = 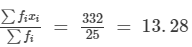
Here, n = 25, which is an odd number. Therefore,
Median = Value of 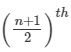 observation = the 13th observation = 13.
observation = the 13th observation = 13.
Now,
Mode = 3 Median - 2 Mean
⇒Mode = 3 x 13 - 2 x (13.28)
⇒Mode = 39 - 26.56
⇒Mode = 12.44.
Question 9:
The following table shows the weights of 12 persons.
| Weight (in kg): | 48 | 50 | 52 | 54 | 58 |
| Number of persons: | 4 | 3 | 2 | 2 | 1 |
Find the median and mean weights. Using empirical relation, calculate its mode.
Answer 9:
Calculation of Mean
| Weight (xi) | 48 | 50 | 52 | 54 | 58 | Total |
| Number of Persons (fi) | 4 | 3 | 2 | 2 | 1 | 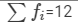 |
| fixi | 192 | 150 | 104 | 108 | 58 | 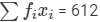 |
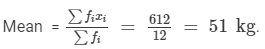
Here, n = 12


Now,
Mode = 3 Median - 2 Mean
⇒ Mode = 3 x 50 - 2 x 51
⇒Mode = 150 - 102
⇒ Mode = 48 kg.
Thus, Mean = 51 kg, Median = 50 kg and Mode = 48 kg.
FAQs on Ex-23.4, Data Handling II Central Values, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the central values in data handling? |  |
| 2. How is the mean calculated in data handling? |  |
| 3. What is the median in data handling? |  |
| 4. How is the mode determined in data handling? |  |
| 5. What do central values indicate in data handling? |  |





















