JEE Advanced (Subjective Type Questions): Equilibrium- 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. A solution contains Na2CO3 and NaHCO3. 10 ml of solution requires 2.5 ml of 0.1 M H2SO4 for neutralisation using phenolphthalein as an indicator. Methyl orange is then added when a further 2.5ml of 0.2M H2SO4 was required. Calculate the amount of Na2CO3 and NaHCO3 in one litre of the solution.
Ans. 5.3 g/l; 4.2 g/l;
Solution. Phenolphthalein indicates half neutralization.
Na2CO3 + H+ → NaHCO3 + Na+ ...(i)
Methyl orange indicates complete neutralisation
NaHCO3 + H+ → Na+ + H2O + CO2 ...(ii)
∴ Volume of 0.1M H2SO4 required for complete neutralisation = 2 × 2.5 = 5.0 ml
0.1 M H2SO4 ≡ 0.2 NH2SO4
[For H2SO4 molarity = 2 × normality]
(∵ Mol. wt. of H2SO4 = 98, and eq. wt. of H2SO4 = 49)
∴ 0.2 M H2SO4 ≡ 0.4 NH2SO4
N1 = normality of Na2CO3, V1 = volume of Na2CO3 = 10 ml,
N2 = normality of H2SO4 = 0.2, V2 = volume of H2SO4 = 5.0 ml
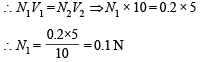
∴ Eq. wt. of 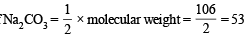
Strength of Na2CO3 = 53 × 0.1 = 5.3 g/l
[∴ strength = normality × Eq. wt]
For neutralization with methyl orange, volume of 0.2 M
H2SO4 used = 2.5 ml = 2.5 ml of 0.4 N H2SO4
= 5 ml of 0.2 N H2SO4 [∴ N1V1 = N2V2]
From 5 ml of 0.2 N H2SO4, 2.5 ml is used for neutralising NaHCO3 formed during first half neutralization Na2CO3
∴ Volume of 0.2N H2SO4 used for neutralisation of NaHCO3 present in original solution = 5.0 – 2.5 = 2.5 ml
∴ N1V1 = N2V2
where N1 = Normality of NaHCO3,
N2 = Normality of H2SO4 = 0.2,
V1 = Volume of NaHCO3 = 10 ml, V2 = Volume of H2SO4 = 2.5 ml
N1V1 = N2V2 ⇒ N1 × 10 = 0.2 × 2.5
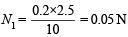
Eq. wt. of NaHCO3 = 84
∴ Strength of NaHCO3 = 84 × 0.05 = 4.2 g/l
Q.2. How many moles of sodium propionate should be added to one litre of an aqueous solution containing 0.020 mole of propionic acid to obtain a buffer solution of pH 4.75? What will be pH if 0.010 mole of hydrogen chloride is dissolved in the above buffer solution. Compare the last pH value with the pH of 0.010 molar HCl solution. Dissociation constant of propionic acid, Ka at 25ºC = 1.34 × 10–5.
Ans. 1.5072 × 10–2 mol, 4.09, 2
Solution. Suppose the number of moles of sodium propionate = x
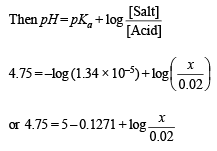
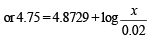
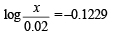
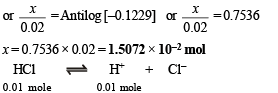
When 0.01 mole of HCl is added, there is (0.01 + 0.02) M of propionic acid and (0.015 – 0.010) M of propionate. Therefore
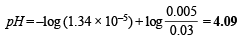
The pH of a 0.010 molar HCl solution = –log 10–2 = 2
Q.3. One mole of nitrogen is mixed with three moles of hydrogen in a 4 litre container. If 0.25 per cent of nitrogen is converted to ammonia by the following reaction
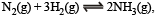
calculate the equilibrium constant (Kc) in concentration units. What will be the value of Kc for the following equilibrium ?
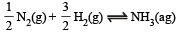
Ans. 1.48 × 10–5 l2 mol–2, 3.82 × 10–3 litre mol–1
Solution.
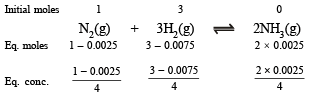
Now we know that 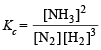
Since 0.0025 and 0.0075 are very small, 1–0.0025 and 3–0.0075 may be taken as 1 and 3 respectively.
Substitute the various values
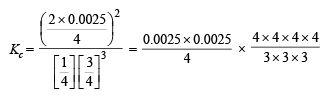
= 1.48 × 10–5 litre2 mol–2
For the equilibrium,
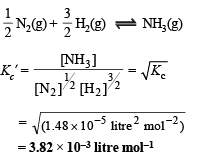
Q.4. Twenty ml. of 0.2 M sodium hydroxide is added to 50 ml. of 0.2 M acetic acid to give 70 ml of the solution. What is the pH of this solution? Calculate the additional volume of 0.2 M NaOH required to make the pH of the solution 4.74. The ionization constant of acetic acid is 1.8 × 10–5.
Ans. 4.5686, 4.86 ml
Solution. TIPS/Formulae :
(i) Find the moles of each species after reaction.
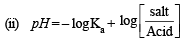
Given, NaOH 0.2 M, 20 ml; CH3COOH 0.2 M, 50 ml Ka = 1.8 × 10–5
V of 0.2M NaOH required to make pH = 4.74 =?
From the chemical reaction
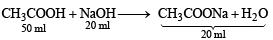
It is evident that 70 ml of the product will contain
(i) 30 ml of 0.2 M unused CH3COOH
[unused CH3COOH = 50 – 20 = 30 ml]
(ii) 20 ml of CH3COONa.
∴ No. of moles of CH3COOH in solution
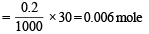
Similarly, No. of moles of CH3COONa solution
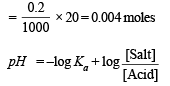
Substituting the values of the various values
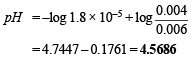
Calculation of the additional volume of 0.2 M NaOH required to make pH of solution 4.74.
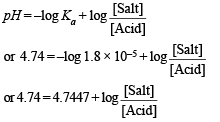
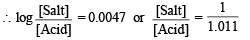
NOTE THIS STEP : Let x ml. be the volume of additional 0.2 M NaOH added to make the pH of the solution 4.74. This will further neutralise x ml. of 0.2 M CH3COOH and produce x ml. of 0.2 M sodium acetate. The resulting solution (70 + x) will now contain
(i) (30 – x) ml of 0.2 M acetic acid.
(ii) (20 + x) ml of 0.2 M sodium acetate.
Number of moles of acetic acid in (70 + x) ml. solution
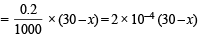
Number of moles of CH3COONa in (70 + x) ml. solution
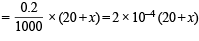
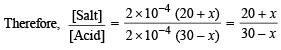
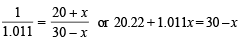
or 1.001 x + x = 30 – 20.22; 2.011x = 9.78 or x = 4.86
Therefore, the additional volume of 0.2 M NaOH required to make the pH of the solution 4.74 is 4.86 ml.
Q.5. The dissociation constant of a weak acid HA is 4.9 × 10–8. After making the necessary approximations, calculate (i) percentage ionization, (ii) pH and (iii) OH– concentration in a decimolar solution of the acid. Water has a pH of 7.
Ans. (i) 7 × 10–2%, (ii) 4.1549, (iii) 1.43 × 10–10 mol/l
Solution. (i) From the dissociation of weak acid HA,
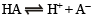
It α is the degree of ionization of the acid HA,
then [H+] = 0.1 α [∵ the acid is decimolar]
[A–]= 0.1 α; [HA] = 0.1 (1 – α)
Therefore,
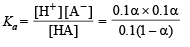
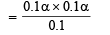 (since acid is weak, 1 – α = 1)
(since acid is weak, 1 – α = 1)

∴ Percentage ionization = 100 × 7 × 10–4 = 7 × 10–2%
(ii) Calculation of pH
[H+] = 0.1a = 0.1 × 7 × 10–4 mole/litre [∵ λ = 7 x 10-4]
= 7 × 10–5 mole/litre
Now since pH = – log [H+] = – log [7 × 10–5]
= 5 – log 7 = 5 – 0.8451 = 4.1549
(iii) Concentration of OH– in decimolar solution
[H+] = 7 × 10–5 mole per litre
Now, Kw = [H+] [OH–] or 1.0 × 10–14 = 7 × 10–5 × [OH–]
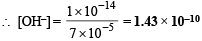 mole per litre
mole per litre
Q.6. A solution contains a mixture of Ag (0.10 M) and Hg2++ (0.10 M) which are to be separated by selective precipitation.
Calculate the maximum concentration of iodide ion at which one of them gets precipitated almost completely. What percentage of that metal ion is precipitated?
[Ksp : AgI = 8.5 × 10–17; Hg2I2 = 2.5 × 10–26]
Ans. 5.0 × 10–13 M, 99.83%
Solution. TIPS/Formulae :
For precipitation to occur ionic product > Ksp.
Mixture solution contains 0.1 M Ag+ and 0.1 Mg Hg22+.
Ksp of Hg2I2 = 2.5 × 10–26 is much smaller than Ksp of AgI which is 8.5 × 10–17.
[I–] concentration needed to precipitate Hg2I2 is calculated as :
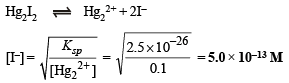
Similarly, [I–] concentration needed to precipitate AgI is :
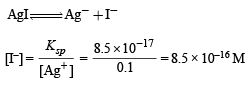
NOTE : Since [I–] concentration needed to ppt. AgI is smaller than that needed to ppt. Hg2I2, AgI is completely precipitated first. AgI starts precipitation with [I–] = 8.5 × 10–16 M.
However, Hg2I2 starts precipitating with AgI only when molar concentration of I– reaches 5.0 × 10–13 M.
[Ag+] left when Hg2I2 begins to ppt. is given by
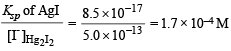
Thus % [Ag+] left unprecipitated 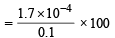
= 0.17%
Hence % Ag+ precipitated = 99.83%
Q.7. One mole of Cl2 and 3 moles of PCl5 are placed in a 100 litre vessel heated to 227ºC. The equilibrium pressure is 2.05 atmosphere. Assuming ideal behaviour, calculate the degree of dissociation for PCl5 and Kp for the reaction :
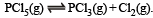
Ans. 33.3%, 0.41
Solution. Let x be the degree of dissociation of PCl5(g), then
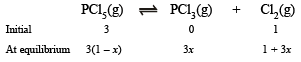
∴ Total number of moles at equilibrium
= 3 (1 – x) + 3x + 1 + 3x = 3 (1 + x) + 1
Using the gas equation : PV = nRT
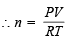
Here, P = 2.05 atm., V = 100 litres, R = 0.082 atm/deg.,
T = 273 + 227 = 500 K
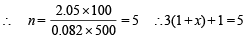
or 3 + 3x + 1 = 5 or 3x = 5 – 4 or 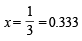
Hence perecentage dissociation of PCl5 = 0.333 × 100 = 33.3%
Calculation of KP for the reaction :
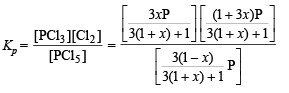
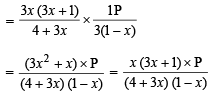
Substituting, x = 1/3 and P = 2.05 atm., we get
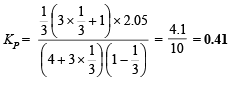
Q.8. Arrange the following in :
(i) increasing bond length : F2, N2, Cl2, O2
(ii) increasing acid strength : HClO3, HClO4, HClO2, HClO
(iii) increasing basicity : H2O, OH–, CH3OH, CH3O–
(iv) Arrange the following oxides in the decreasing order of Bronsted basicity :
BaO, SO3, CO2, Cl2O7, B2O3
Ans. (i) N2 < O2 < F2 < Cl2,
(ii) HClO < HClO2 < HClO3 < HClO4
(iii) H2O < CH3OH < OH– < CH3O–
(iv) BaO > B2O3 > CO2 > SO3 > Cl2O7
Solution. (i) N2 < O2 < F2 < Cl2
i.e., N ≡ N ;O <O ; F,F ; Cl,Cl
NOTE :
As the number of bonds increases the bond length decreases.
So N2 < O2 < halogens. Among F2 and Cl2 bond length of Cl2 will be higher because of higher atomic radii.
(ii) Among oxyacids of the same element, acidic nature increases with its oxidation number, e.g.,

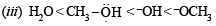
Weaker the base stronger is its conjugate acids
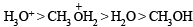 (Decreasing acidic order of the conjugate bases.)
(Decreasing acidic order of the conjugate bases.)
(iv) BaO > B2O3 > CO2 > SO3 > Cl2O7
Basicity increases with increase in oxidation state
(Ba = +2, B = +3, C = +4, S = +6, Cl = +7).
Q.9. The [H+] in 0.2 M solution of formic acid is 6.4 × 10–3 mole litre–1. To this solution sodium formate is added so as to adjust the concentration of sodium formate to one mole litre–1. What wil be pH of this solution? Ka for HCOOH is 2.4 × 10–4 and degree of dissociation of HCOONa is 0.75.
Ans. 4.19
Solution. TIPS/Formulae :
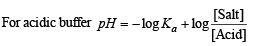
Calculation of concentration of HCOOH.
Here, c = 0.2 M; [H+] = 6.4 × 10–3
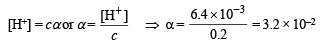
NOTE : Thus the degree of dissociation of HCOOH is very low which on addition of sodium formate is further suppressed due to common ion effect.
Since the degree of dissociation is very low (3.2 × 10–2), it can be neglected and hence [HCOOH] can be taken as 0.2 M.
Calculation of concentration of HCOO–, [HCOO–]
It can be obtained in the following manner :
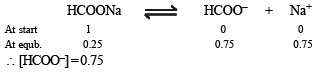
For acidic buffer 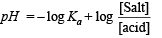
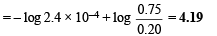
Q.10. The equilibrium constant of the reaction

at 100ºC is 50. If a one litre flask containing one mole of A2 is connected to a two litre flask containing two mole of B2, how many mole of AB will be formed at 373ºC?
Ans. 1.886
Solution.
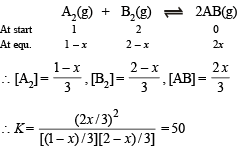
On solving we get, 23x2 – 75x + 50 = 0; x = 2.317 or 0.943
The value 2.317 is inadmissable because initial concentration of reactants is 2 moles and so x = 0.943
∴ Moles of AB formed = 2 × 0.943 = 1.886
Q.11. The solubility of Mg(OH)2 in pure water is 9.57×10–3 g/litre. Calculate its solubility (in g/litre) in 0.02 M Mg(NO3)2 solution.
Ans. 8.7 × 10–4 g/litre
Solution. Solubility of Mg(OH)2 in water
S = 9.57 × 10–3 g/litre 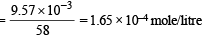
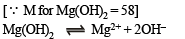
Ksp = (S) (2S)2 = 4S3 = 4 (1.65 × 10–4)3 = 1.8 × 10–11 approx.
Calculation of solubility of Mg(OH)2, say, x, in Mg(NO3)2 or [Mg2+] = x + 0.02; [OH–] = x
Ksp = [Mg2+] [2OH–]2 or 1.8 × 10–11 = (x + 0.02) (2x)2
Neglecting x in comparison to 0.02 (common ion effect)
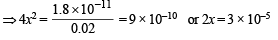
x = 1.5 × 10–5 moles/litres
= 1.5 × 58 × 10–5 = 8.7 × 10–4 g/litre.
Q.12. What is the pH of the solution when 0.20 mole of hydrochloric acid is added to one litre of a solution containing.
(i) 1 M each of acetic acid and acetate ion?
(ii) 0.1 M each of acetic acid and acetate ion?
Assume the total volume is one litre.
Ka for acetic acid = 1.8 × 10–5.
Ans. 4.5686, 1
Solution. (i) Amount of HCl added = 0.20 mole
[H+] = 0.2 g litre–1
NOTE : Added H+ ions will combine with the acetate ions forming acetic acid with the result concentration of acetate ions will decrease while that of acetic acid will increase.
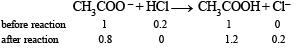
∴ Concentration of acetate ions after adding 0.20 mole of HCl.
[CH3COO–] = 1.0 – 0.2 = 0.8 mole
Similarly, concentration of acetic acid,
[CH3COOH] = 1.0 + 0.2 = 1.2 mole
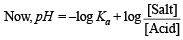
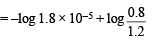
pH = 4.7447 + 0.3010 – 0.4771 = 4.5686
(ii) Amount of HCl added = 0.20 mole
Out of 0.2 mole of [H+] added, 0.1 mole will combine with 0.1 mole of CH3COO– forming 0 mole of CH3COOH.
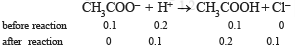
∴ Total concentration of acetic acid [CH3COOH]
= 0.1 + 0.1 = 0.2 mole
In presence of [H+], CH3COOH will not ionize.
Therefore, pH of the solution will be due to the presence of H+ of HCl, i.e. 0.2 – 0.1 = 0.1 mole HCl
pH = –log [H+] = –log [0.1] = 1
Q.13. At a certain temperature equilibrium constant (Kc) is 16 for the reaction.
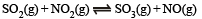
If we take one mole each of all the four gases in a one litre container, what would be the equilibrium concentrations of NO(g) and NO2(g)?
Ans. 1.6 moles, 0.4 moles
Solution. Initial concentration of each gas = 1 mole
Let the No. of moles of NO2 reacted at equilibrium = x
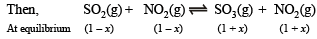
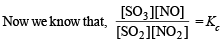
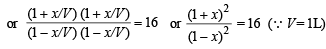
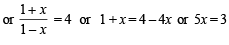
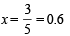
∴ Thus the concentration of NO at equilibrium
= 1 + x = 1 + 0.6 = 1.6 moles
Concentration of NO2 at equilibrium
= 1 – x = 1 – 0.6 = 0.4 moles
Q.14. N2O4 is 25% dissociated at 37ºC and one atmosph er e pressure. Calculate (i) Kp and (ii) the percentage dissociation at 0.1 atmosphere and 37ºC.
Ans. 0.266 atm, 64%
Solution. (i)
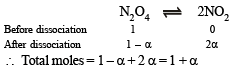
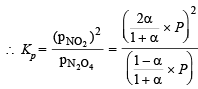
where P is total pressure
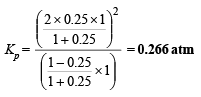 [∵ a = 0.25]
[∵ a = 0.25]
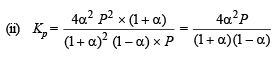
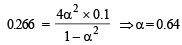
∴ Percentage dissociation = 63 %
Q.15. How many gram-mole of HCl will be required to prepare one litre of buffer solution (containing NaCN and HCl) of pH 8.5 using 0.01 gram formula weight of NaCN?
K dissociation (HCN) = 4.1 × 10–10.
Ans. 8.85 × 10–3 M
Solution. TIPS/Formulae :
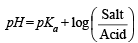
If x moles of HCl are added then they will combine with
NaCN to form x moles of very weak acid HCN.
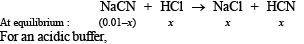
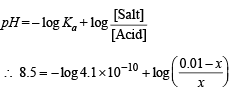
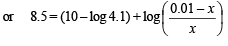
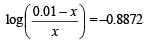 [log 4.1 = 0.6128]
[log 4.1 = 0.6128]
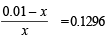
x = 8.85 × 10–3 M = 8.85 × 10–3 moles of HC
Q.16. The equilibrium constant Kp of the reaction :
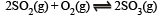
is 900 atm. at 800 K. A mixture containing SO3 and O2 having initial partial pressure of 1 and 2 atm. respectively is heated at constant volume to equilibrate. Calculate the partial pressure of each gas at 800 K.
Ans.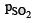 = 0.0236 atm,
= 0.0236 atm, 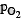 = 2.0118 atm,
= 2.0118 atm, 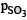 = 0.9764 atm
= 0.9764 atm
Solution. NOTE : Since the reaction is carried out at constant volume, change in partial pressure of a species will be directly proportional to the change in its amount. Hence, we can write
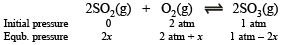
Where 2 x is th e change in par tial pr essure of SO3 at equilibrium.
Substituting the expression of partial pressure in the expression. For Kb, we get
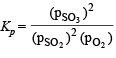
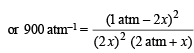
Assuming x is very small as compared to 1
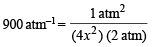
On usual calculations, x = 0.0118 atm
Thus 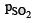 = 2x = 2 × 0.0118 atm = 0.0236 atm
= 2x = 2 × 0.0118 atm = 0.0236 atm
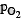 = 2 atm + x = 2 + 0.0118 = 2.0118 atm
= 2 atm + x = 2 + 0.0118 = 2.0118 atm
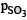 = 1 atm – 2x = 1 – 0.0236 = 0.9764 atm
= 1 atm – 2x = 1 – 0.0236 = 0.9764 atm
Q.17. Freshly precipitated aluminium and magnesium hydroxides are stirred vigorously in a buffer solution containing 0.25 mole/l of ammonium chloride and 0.05 mole/l of ammonium hydroxide. Calculate the concentration of aluminium and magnesium ions in solution:
Kb[NH4OH] = 1.80 × 10–5
Ksp [Mg(OH)2] = 6 × 10–10
Ksp [Al(OH)3] = 6 × 10–32
Ans. 46.29 mol ion/l, 1.286 × 10–15 mol ion/l
Solution. TIPS/Formulae :
p(OH) for basic buffer 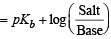
We know that 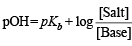
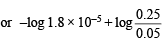
pOH = 5 – log 1.8 + log 5 = 5.6989 – 0.2552
– log [OH–] = 5.4437; log [OH–] = –5.4437
[OH–] = 3.5999 × 10–6 [Taking antilog]
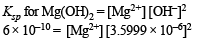
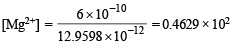
= 46.29 mole ion per litre
Ksp for Al(OH)3 = [Al3+] [OH–]3
6 × 10–32 = [Al3+] (3.5999 × 10–6)3
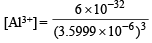 = 1.286 × 10–15 mol ion/l
= 1.286 × 10–15 mol ion/l
Q.18. For the reaction : 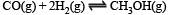
hydrogen gas is introduced into a five litre flask at 327ºC, containing 0.2 mole of CO(g) and a catalyst, until the pressure is 4.92 atm. At this point 0.1 mole of CH3OH(g) is formed. Calculate the equilibrium constant, Kp and Kc.
Ans. 277.78 mol–2 l2, 0.1144 atm–2
Solution. Let the total number of moles of all gases at equilibrium point = n
P = 4.92 atm. V = 5l
R = 0.0821 atm. l mol–1 K–1 T = 273 + 327 = 600K
By applying the formula PV = nRT
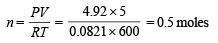
(i) Calculation of the number of moles of the individual gases at equilibrium point.
No. of moles of CH3OH formed = 0.1 (Given)
∴ No. of moles of CO (also) = 0.1
[∴ moles of CO = moles of CH3OH formed]
Hence No. of moles of H2 = 0.5 – (0.1 + 0.1) = 0.3
∴ Molar concentration of various species will be
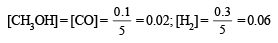
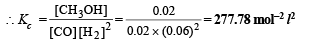
(ii) Calculation of Kp. We know that
Kp = Kc × (RT)Δn = 277.78 × (0.0821 × 600)–2 (Δn = 1 – 3 = –2)
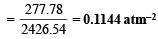
Q.19. What is the pH of 1.0 M solution of acetic acid? To what volume must one liter of this solution be diluted so that the pH of the resulting solution will be twice the original value? Given : Ka = 1.8 × 10–5.
Ans. 2.3724, 2.78 × 104 litres
Solution.
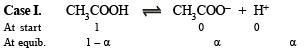
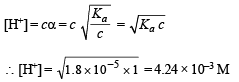
Thus pH = – log H+ = –log 4.24 × 10–3 = 2.3724
Case II. pH after dilution = 2 × original pH
= 2 × 2.3724 = 4.7448
Let conc. after dilution = c1
and degree of dissociation = α1
Since pH = – log [H+]
4.7448 = – log [H+]
[H+] = 1.8 × 10–5 = c1α1 ∴ c1α1 = 1.8 × 10–5
Dissociation constant
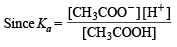
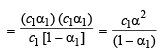
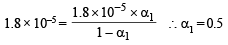
Substituting the value of α1 in the following relation
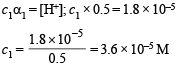
Since the number of moles of CH3COOH before and after dilution will be same
∴ Mole of CH3COOH before dilution = Mole of CH3COOH after dilute

Q.20. The solubility product of Ag2C2O4 at 25ºC is 1.29 × 10–11 mol3 l–3. A solution of K2C2O4 containing 0.1520 mole in 500 ml water is shaken at 25ºC with excess of Ag2CO3 till the following equilibrium is reached :

At equilibrium the solution contains 0.0358 mole of K2CO3.
Assuming the degree of dissociation of K2C2O4 and K2CO3 to be equal, calculate the solubility product of Ag2CO3.
Ans. 3.794 × 10–12 mol3 l–3
Solution.
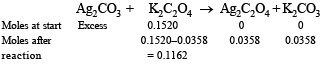
Molar concentration of 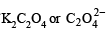 left unreacted
left unreacted
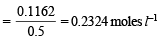 [∵ 500 ml = 0.5 L ]
[∵ 500 ml = 0.5 L ]
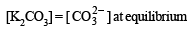
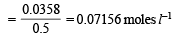
Given that Ksp for Ag2C2O4 = 1.29 × 10–11 mol3 l–3 at 25ºC
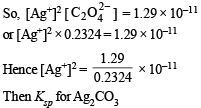

|
446 docs|929 tests
|





















