Page No.5.5 & 5.6, Negative Numbers And Integers, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
PAGE NO 5.5:
Question 1: Write the opposite of each of the following:
(i) Increase in population
(ii) Depositing money in a bank
(iii) Earning money
(iv) Going North
(v) Gaining a weight of 4 kg
(vi) A loss of Rs 1000
(vii) 25
(viii) −15
ANSWER:
(i) Decrease in population
(ii)Withdrawing money from a bank
(iii) Spending money
(iv) Going South
(v) Losing weight of 4 kg
(vi) A gain of Rs 1,000
(vii) −25
(viii) 15
Question 2: Indicate the following by using intergers:
(ii) 5050 below zero
(iii) A profit of Rs 800
(iv) A deposit of Rs 2500
(v) 3 km above sea level
(vi) 2 km below sea level
ANSWER:
(i) If temperature is above zero, then it should be positive, i.e., +25°.
(ii) If temperature is below zero, then it should be negative, i.e., 5°.
(iii) If there is a profit of Rs 800, then it should be +800.
(iv) Deposition of Rs 2,500 indicates that money in the account is increased; therefore, it should be +2500 .
(v) Here, the distance is above the sea level; therefore, it should be +3.
(vi) Here, the distance is below the sea level; therefore, it should be −2.
Question 3: Mark the following integers on a number line:
(ii) −4
(iii) 0
ANSWER:
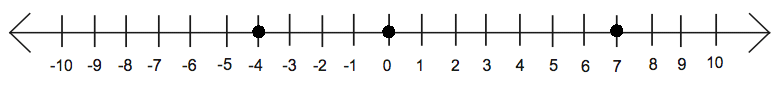
Question 4: Which number in each of the following pairs is smaller?
(i) 0, −4
(ii) −3, 13
(iii) 8, 13
(iv) −15, −27
ANSWER:
(i) 0 is greater than every negative integer, so −4 < 0.
(ii) Every positive integer is greater than every negative integer; therefore, −3 < 12.
(iii) Because 8 is to the left of 13 on a number line, 8 < 13.
(iv) Because −27 is to the left of −15 on a number line, −27 < −15.
Question 5: Which number in each of the following pairs is larger?
(ii) −12, −8
(iii) 0, 7
(iv) 12, −18
ANSWER:
(i) Every positive integer is greater than every negative integer; therefore, 3 > −4.
(ii) Because −12 is to the left of −8 on a number line, −8 > −12.
(iii) Every positive integer is greater than zero; therefore, 7 > 0.
(iv) Every positive integer is greater than every negative integer; therefore, 12 > −18.
Question 6: Write all integers between:
(ii) −2 and 2
(iii) −4 and 0
(iv) 0 and 3
ANSWER:
(i) There are nine integers in between −7 and 3, namely, −6, −5, −4, −3, −2, −1, 0, 1 and 2.
(ii) There are three integers in between −2 and 2, namely, −1, 0 and 1.
(iii) There are three integers in between −4 and 0, namely, −3, −2 and −1.
(iv) There are two integers in between 0 and 3, namely, 1 and 2.
Question 7: How many integers are between?
(ii) 5 and 12
(iii) −9 and −2
(iv) 0 and 5
ANSWER:
(i) There are six integers in between −4 and 3, namely, −3, −2, −1, 0, 1 and 2.
(ii) There are six integers in between 5 and 12, namely, 6, 7, 8, 9, 10 and 11.
(iii) There are six integers in between −9 and −2, namely, −8, −7, −6, −5, −4 and −3.
(iv) There are four integers in between 0 and 5, namely, 1, 2, 3 and 4.
Question 8: Replace * in each of the following by < or > so that the statement is true:
(ii) 0 * 3
(iii) 0 * −7
(iv) −18 * 15
(v) −235 * −532
(vi) −20 * 20
ANSWER: In the given pairs of numbers, the numbers that are to the left of the other numbers on a number line are smaller.
(i) 2 < 5
(ii) 0 < 3
(iii) 0 > −7
(iv) −18 < 15
(v) −235 > −532
(vi) −20 < 20
Question 9:Write the following integers in increasing order:
(i) −8, 5, 0, −12, 1, −9, 15
(ii) −106, 107, −320, −7, 185
ANSWER: (i) −12 < −9 < −8 < 0 < 1 < 5 < 15
(ii) −320 < −106 < −7 < 107 < 185
Question 10: Write the following integers in decreasing order:
(ii) −154, 123, −205, −89, −74
ANSWER: (i) 8 > 7 > 6 > 0 > −2 > −5 > −9 > −15
(ii) 123 > −74 > −89 > −154 > −205
Question 11: Using the number line, write integer which is:
(ii) 5 less than 3
(iii) 4more than −9
ANSWER: (i) We want an integer two more than 3. So, on the number line, we will start from 3 and move 2 units to the right to obtain 5, as shown on the number line.
(ii) We want an integer five less than 3. So, on the number line, we will start from 3 and move 5 units to the left to obtain −2, as shown on the number line.
(iii) We want an integer four more than −9. So, on the number line, we will start from −9 and move 4 units to the right to obtain −5, as shown on the number line.
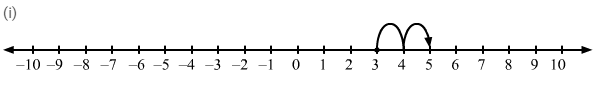
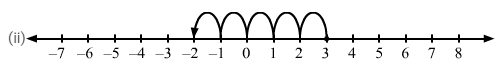
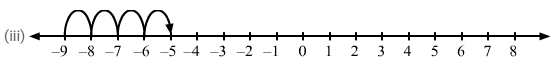
Question 12:Write the absolute value of each of the following:
(i) 14
(ii) −25
(iii) 0
(iv) −125
(v) −248
(vi) a −7, if a is greater than 7
(vii) a −7, if a −2 is less than 7
(viii) a + 4, if a is greater than −4
(ix) a + 4, if a is less than −4
(x) |−3|-3
(xi) −|−5|--5
(xii) |12−5|12-5
ANSWER: (i) Absolute value of 14 is 14.
(ii) Absolute value of −25 is 25.
(iii) Absolute value of 0 is 0.
(iv) Absolute value of −125 is 125.
(v) Absolute value of −248 is 248.
(vi) Absolute value of (a − 7) is (a − 7) if a is greater than 7, that is, a − 7 > 0.
(vii) if a − 2 is less than 7, that is, a − 2 < 7 ⇒ a < 9 or a − 7 < 2
So absolute value of a−7 = a−7 if 7 < a < 9 that is a−2 is less than 7 but a−2 is greater than 5.
and absolute value will be −(a−7) if a < 7 if a−7 is less than 5.
(viii) Absolute value of (a + 4) is (a + 4) if a is greater than −4, that is, a > −4 ⇒ a + 4 > 0.
(ix) Absolute value of (a + 4) is −(a + 4) if a is less than −4, that is, a < −4 ⇒ a + 4 < 0.
(x) Absolute value of −3 is 3.
(xi) −|−5| is −5 and its absolute value is 5.
(xii) |12 − 5 | = | 7| and its absolute value is 7.
Question 13: (i) Write 4 negative integers less than −10.
(ii) Write 6 negative integers just greater than −12.
ANSWER: (i) −9, −8, −7 and −6 are the four negative integers less than −10.
(ii) −11, −10, −9, −8, −7 and −6 are the six negative integers just greater than −12.
Question 14: Which of the following statements are true?
(ii) The opposite of zero is zero.
(iii) Zero is not an integer.
(iv) 0 is larger than every negative integer.
(v) The absolute value of an integer is greater than the integer.
(vi) A positive integer is greater than its opposite.
(vii) Every negative integer is less than every natural number.
(viii) 0 is the smallest positive integer.
ANSWER:
(i) False
Integers are negative also.
(ii) True
0 is neither positive nor negative.
(iii) False
0 is simply an integer that is neither positive nor negative.
(iv) True
Every negative integer is to the left of 0 on a number line.
(v) False
The absolute value of positive integer is integer itself. So both are equal.
(vi) True
Its opposite will be a negative integer and positive integer is always greater than negative integer.
(vii) True
Natural numbers start from 0, and 0 is greater than every negative integer.
(viii) False
0 is neither positive nor negative.
FAQs on Page No.5.5 & 5.6, Negative Numbers And Integers, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What are negative numbers? |  |
| 2. How are negative numbers used in real life? |  |
| 3. What is the difference between negative numbers and integers? |  |
| 4. How do we add and subtract negative numbers? |  |
| 5. Can negative numbers be multiplied or divided? |  |





















