Deriving the centripetal acceleration formula - Class 11 PDF Download
What is centripetal acceleration and derive its formula also?
Ref: https://edurev.in/question/702216/What-is-centripetal-acceleration-and-derive-its-formula-also-
A body that moves in a circular motion (of radius r) at constant speed (v) is always being accelerated. The acceleration is at right angles to the direction of motion (towards the center of the circle) and of magnitude v2 / r.
The direction of acceleration is deduced by symmetry arguments. If the acceleration pointed out of the plane of the circle, then the body would leave the plane of the circle; it doesn't, so it isn't. If the acceleration pointed in any direction other than perpendicular (left or right) then the body would speed up or slow down. It doesn't.
Now for the magnitude. Consider the distance traveled by the body over a small time increment Δt:
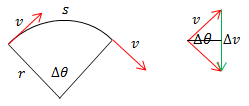
We can calculate the arc length s as both the distance traveled (distance = rate * time = v Δt) and using the definition of a radian (arc = radius * angle in radians = r Δθ:)
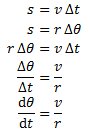
The angular velocity of the object is thus v / r (in radians per unit of time.)
The right half of the diagram is formed by putting the tails of the two v vectors together. Note that Δθ is the same in both diagrams.
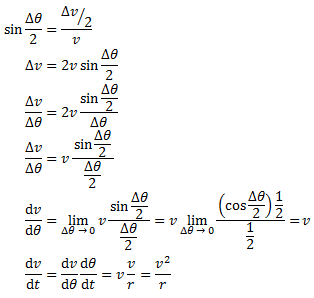
FAQs on Deriving the centripetal acceleration formula - Class 11
| 1. How can I derive the centripetal acceleration formula? |  |
| 2. What is the significance of centripetal acceleration? |  |
| 3. How does centripetal acceleration differ from tangential acceleration? |  |
| 4. Can centripetal acceleration ever be zero? |  |
| 5. How does centripetal acceleration relate to centripetal force? |  |















