The Triangles and its properties Class 7 Worksheet Maths
Q.1. Which of the following figures will have its altitude outside the triangle?
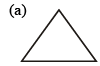
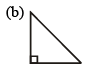
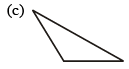

 View Answer
View AnswerAns. C
Q.2. Fill up the blanks : (i) Every triangle has at least ................. acute angles.
(ii) The longest side of a right-angled triangle is called its ...............
(iii) Median is also called .................. in an equilateral triangle.
(iv) The line segment joining a vertex of a triangle to the mid-point of its opposite side is called its.............
 View Answer
View AnswerAns. (i) 2
(ii) Hypotenuse
(iii) Altitude or Perpendicular bisector
(iv) Median
Q.3. If one angle of a triangle is 60° and the other two angles are in the ratio 1: 2, then find the angles.
 View Answer
View AnswerAns.
Given one angle of the triangle is 60°, and the other two angles are in the ratio 1:2, let the angles be x and 2x.
The sum of the angles in a triangle is 180°:
x + 2x + 60° = 180°
Simplifying:
3x = 120°
Dividing by 3:
x = 40°
Thus, the angles of the triangle are 60°, 40°, and 80°.
Q.4. In figure find the value of ∠A + ∠B + ∠C + ∠D + ∠E + ∠F
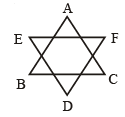
 View Answer
View AnswerAns.
In the given star-shaped figure, the angles at the vertices (∠A, ∠B, ∠C, ∠D, ∠E, ∠F) are formed by intersecting lines. The sum of the angles around a point in any polygon is 360°.
Thus, the value of ∠A + ∠B + ∠C + ∠D + ∠E + ∠F is 360°.
Q.5. Two poles of 8m and 14m stand upright on a plane ground. If the distance between the two tops is 10m.
Find the distance between their feet.
 View Answer
View AnswerAns.
The height difference between the two poles is 14m - 8m = 6m. Using the Pythagorean theorem:
(Base)² + (Height Difference)² = (Distance Between Tops)²
Let the base be x. So,
x² + 6² = 10²
x² + 36 = 100
x² = 64, therefore x = 8m.
The distance between their feet is 8 meters.
Q.6. Mohini walks 1200m due East and then 500m due North. How far is she from her starting point?
 View Answer
View AnswerAns.
Mohini walks 1200m east and then 500m north. This forms a right-angled triangle, where the horizontal distance is 1200m, and the vertical distance is 500m.
Using the Pythagorean theorem:
Distance² = (1200)² + (500)²
Distance² = 1440000 + 250000
Distance² = 1690000
Taking the square root:
Distance = √1690000 = 1300m
So, Mohini is 1300 meters away from her starting point.
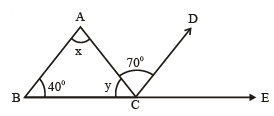
Q.7. Find the value of x and y. (i) Here CD || AB
(ii)
(iii)
(iv)
 View Answer
View AnswerAns. (i)
x = 70° (Corresponding Angle)
70° + 40° + y = 180°
So, x = 180° - 110° = 70°.
Hence, x = 70° , y = 70°
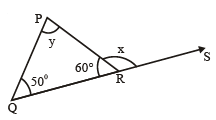
(ii)
x + 60° = 180° (Linear Pair)x = 180 - 60° x = 120°
y + 50° = 120° (Exterior Angle Property)
So, y = 120° - 50° = 70°.
Thus, y = 70° and x = 120°.
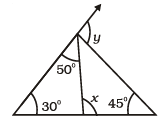
(iii) 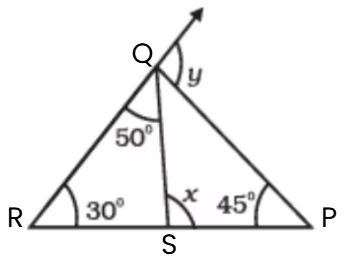 x =50° + 30° = 80° (Exterior Angles Property)
x =50° + 30° = 80° (Exterior Angles Property)
In Triangle PQR, 30° + 45° + ∠Q = 180° (Angle sum property)
∠Q = 180° - 75° = 105°
∠Q = 105°
In Triangle QSP,
80° + 45° + ∠SQP = 180° (Angle sum property)
125° + ∠SQP = 180°
∠SQP = 180° - 125° = 55°
50° + 55° + y = 180°
y = 180° - 105° = 75°
x = 80° , y = 75°
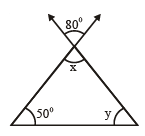
(iv) x = 80° (Vertically Opposite angle)
y + 50° + 80° = 180° (Angle sum property)
y = 180° - 130° = 50°
x = 80°, y = 50°
Q.8. Find the value of x :
(i)
(ii)
(iii)
(iv)
 View Answer
View AnswerAns. (i)
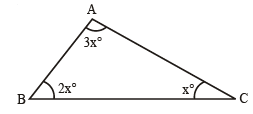
Given angles: 3x°, 2x°, and x°.
Using the angle sum property of a triangle:
3x° + 2x° + x° = 180°6x° = 180°x = 180° / 6 = 30°
- x = 30°
- 3x = 90°
- 2x = 60°
(ii)
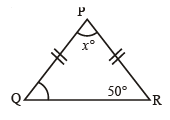
- Given angles: 50°, 50°, and x°.
- Using the angle sum property of a triangle:
50° + 50° + x° = 180°
x° + 100° = 180°
x° = 100°
x = 100° / 2 = 50°
Therefore, the angles x = 50°
(iii)
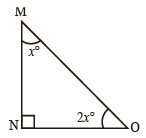
- Given angles: x°, 2x°, and a right angle (90°).
- Using the angle sum property of a triangle:
x° + 2x° + 90° = 180°
3x° = 90°
x = 90° / 3 = 30° - Therefore, the angles are:
- x = 30°
- 2x = 60°
Thus, the values for each triangle are: x = 30°, 2x = 60°
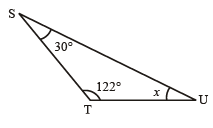
(iv)
Given angles: 30°, 122°, and x°.
Using the angle sum property of a triangle:30° + 122° + x° = 180°
Simplifying:152° + x° = 180°
Now, subtract 152° from both sides:x° = 180° - 152° = 28°
Thus, the value of x is 28°
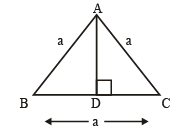
Q.9. ABC is an equilateral triangle with side a. AD is an altitude. Find the value of AD2.
 View Answer
View AnswerAns. AD2 =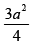
Q.10. State whether the given statements are True or False :
(i) Sum of two sides of a triangle is greater than or equal to the third side.
(ii) The difference between the lengths of any two sides of a triangle is smaller than the length of third side.
(iii) Sum of any two angles of a triangle is always greater than the third angle.
(iv) It is possible to have a right-angled equilateral triangle.
 View Answer
View AnswerAns. (i) False
(ii) True
(iii) False
(iv) False
|
77 videos|388 docs|39 tests
|
FAQs on The Triangles and its properties Class 7 Worksheet Maths
| 1. What are the different types of triangles based on their sides? |  |
| 2. What are the different types of triangles based on their angles? |  |
| 3. How can I calculate the area of a triangle? |  |
| 4. What is the Pythagorean theorem and how does it relate to right triangles? |  |
| 5. What are the properties of similar triangles? |  |




















