JEE Advanced (Subjective Type Questions): Laws of Motion | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. In the diagram shown, the blocks A, B and C weight, 3 kg, 4 kg and 5 kg respectively. The coefficient of sliding friction between any two surface is 0.25. A is held at rest by a massless rigid rod fixed to the wall while B and C are connected by a light flexible cord passing around a frictionless pulley. Find the force F necessary to drag C along the horizontal surface to the left at constant speed. Assume that the arrangement shown in the diagram, B on C and A on B, is maintained all through. (g = 9.8 m/s2)
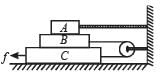
Ans. 71.05 N
Solution. When force F is applied on C, the block C will move towards left.
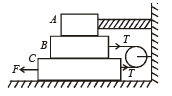
The F.B.D. for mass C is
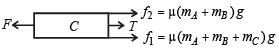
As C is moving with constant speed F = f1 + f2 + T ... (i) F.B.D. for mass B is
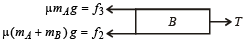
As B is moving with constant speed f2 + f3 = T (ii) Subtracting (ii) from (i)
F – (f2 + f3) = f1 + f2 + T – T = f1 + f2
⇒ F = f1 + 2f2 + f3 = µ (mA + mB + mC) g + 2µ (mA + mB) g + µ mAg
F = µ (4 mA + 3 mB + mC) g
= 0.25 [4 × 3 + 3 × 4 + 5] × 9.8 = 71.05 N
Q.2. Two cubes of masses m1 and m2 be on two frictionless slopes of block A which rests on a horizontal table. The cubes are connected by a string which passes over a pulley as shown in the figure.
To what horizontal acceleration f should the whole system (that is blocks and cubes) be subjected so that the cubes do not slide down the planes.
What is the tension of the string in this situation? (1978)
Ans.
Solution. Without Pseudo Force
F.B.D for mass m2
N2 cos β = T sin β + m2g ... (i)
and (N2 sin β + T cos β) = m2 f ... (ii)
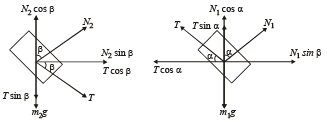
FBD for mass m1
N1 cos α + T sin α = m1g ... (iii)
and (N1 sin α – T cos α) = m1 f ... (iv)
On solving the four equations, we get the above results.
Q.3. A horizontal uniform rope of length L, resting on a frictionless horizontal surface, is pulled at one end by force F. What is the tension in the rope at a distance l from the end where the force is applied? (1978)
Ans.
Solution.
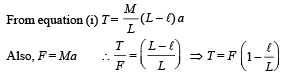
Q.4. Masses M1, M2 and M3 are connected by strings of negligible mass which pass over massless and friction less pulleys P1 and P2 as shown in fig The masses move such that the portion of the string between P1 and P2 in parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. (1981- 6 Marks)
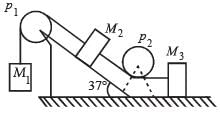
If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1
(ii) The tension in the horizontal portion of the string
Ans. 4.2 Kg, 9.8 N
Solution. (a) If M1, M2 and M3 are considered as a system, then the force responsible to more them is M1g and the retarding force is (M2g sinθ + µM2g cosθ + µM3g). These two should be equal as the system is moving with constant velocity.
Q.5. A particle of mass m rests on a horizontal floor with which it has a coefficient of static friction μ . It is desired to make the body move by applying the minimum possible force F. Find the maguitude of F and the direction in which it has to be applied. (1987 - 7 Marks)
Ans. mgsinθ, tan–1μ
Solution. Let F be the force applied to move the body at an angle θ to the horizontal.
The body will move when
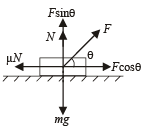
F cos θ = µN ... (i)
Applying equilibrium of forces in the vertical direction we get
F sin θ + N = mg
⇒ N = mg – F sin θ ... (ii)
⇒ From (i) and (ii)
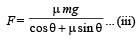
Differentiating the above equation w.r.t. θ , we get
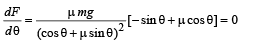
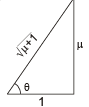
⇒ θ = tan–1µ
This is the angle for minimum force.
To find the minimum force substituting these values in equation (iii)
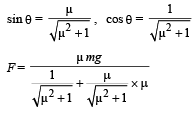
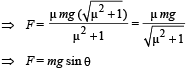
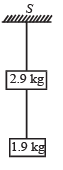
Q.6. Two blocks of mass 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 meter, see fig. The upper wire has negligible mass and the lower wire has a uniform mass of 0.2 kg/m.
The whole system of blocks wires and support have an upward acceleration of 0.2 m/s2. Acceleration due to gravity is 9.8 m/s2. (1989 - 6 Marks)
(i) Find the tension at the mid-point of the lower wire.
(ii) Find the tension at the mid-point of the upper wire.
Ans. 20N, 50N
Solution. Let λ be the mass per unit length of lower wire.
Let us consider the dotted portion as a system and the tension T accelerates the system upwards
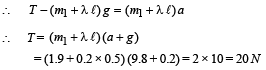
To find tension T ' Let us consider the dotted portion given in figure (2)
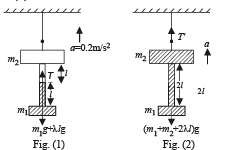
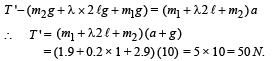
Alternatively considering m1, m2 and lower wire as a system T' – 5 g = 5 a
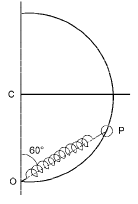
Q.7. A smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length 3R/4 is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held stationary at point P such that the spring makes an angle of 60° with the vertical. The spring constant K= mg/R.
Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction. (1996 - 5 Marks)
Ans.
Solution.
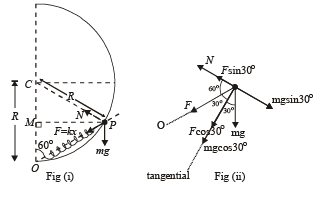
In DOCP, OC = CP = R
∴ ∠COP = ∠CPO = 60° ⇒ ∠OCP = 60°
∴ ΔOCP is an equilateral triangle ⇒ OP = R
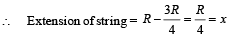
The forces acting are shown in the figure (i)
The free body diagram of the ring is shown in fig. (ii)
Force in the tangential direction
= F cos 30° + mg cos 30
= [kx + mg] cos 30°
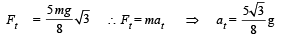
Also, when the ring is just released
N + F sin 30° = mg sin 30°
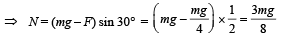
Q.8. A particle of mass 10–2 kg is moving along the positive x axis under the influence of a force F(x) = – K/(2x2) where K = 10–2 N m2. At time t = 0 it is at x = 1.0 m and its velocity is v = 0. (1998 - 8 Marks)
(a) Find its velocity when it reaches x = 0.50 m.
(b) Find the time at which it reaches x = 0.25 m.
Ans.
Solution. m = 10–2 kg, motion is along positive X-axis
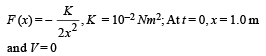
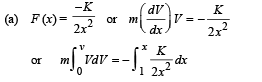
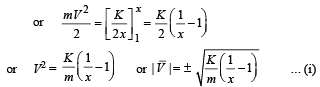
Initially the particle was moving in + X direction at x = 1.
When the particle is at x = 0.5, obviously its velocity will be in –X direction. The force acting in –X direction first decreases the speed of the particle, bring it momentarily at rest and then changes the direction of motion of the particle.
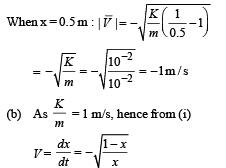
Note : We have chosen –ve sign because force tends to decrease the displacement with time
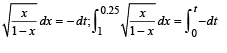
Put x = sin2θ , dx = 2 sin θ cos θ d θ
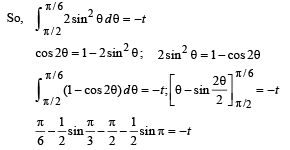
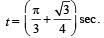
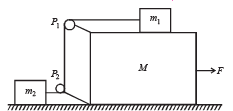
Q.9. In the figure masses m1, m2 and M are 20 kg, 5 kg and 50 kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g = 10 m/s2 (2000 - 10 Marks)
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1 = 2f2. Find f1 and f2.
Write equations of motion of all the masses. Find F, tension in the string and acceleration of the masses
Ans. (b) F = 60 N; T = 18 N
Solution. Given m1 = 20 kg, m2 = 5 kg, M = 50 kg, µ = 0.3 and g = 10 m/s2
(A) Free body diagram of mass M is
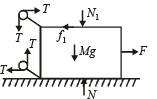
(B) The maximum value of f1 is
(f1)max = (0.3) (20) (10) = 60 N
The maximum value of f2 is (f2)max = (0.3) (5) (10) = 15 N
Forces on m1 and m2 in horizontal direction are as follows :
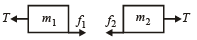
Note : There are only two possibilities.
(1) Either both m1 and m2 will remain stationary (w.r.t. ground) or (2) both m1 and m2 will move (w.r.t. ground). First case is possible when.
T < (f1)max or T < 60 N
and T < (f2)max or T < 15 N
These conditions will be satisfied when T < 15 N say T = 14 then f1 = f2 = 14 N.
Therefore the condition f1 = 2f2 will not be satisfied.
Thus m1 and m2 both can't remain stationary.
In the second case, when m1 and m2 both move
f2 = (f2) max = 15 N
Therefore, f1 = 2f2 = 30 N
Note : Since f1 < (f1)max, there is no relative motion between m1 and M, i.e., all the masses move with same acceleration, say 'a'.
Free body diagrams and equations of motion are as follows:
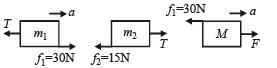
For m1 : 30 – T = 20 a ... (i)
For m2 : T – 15 = 5 a ... (ii)
For M : F – 30 = 50 a ... (iii)
Solving these three equations, we get,
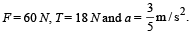
Q.10. Two block A and B of equal masses are placed on rough inclined plane as shown in figure. When and where will the two blocks come on the same line on the inclined plane if they are released simultaneously? Initially the block A is √2 m behin d th e block B. Co-efficien t of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g =10 m/s2). (2004 - Marks)

Ans. 8√2m, 7√2 m, 2 sec.
Solution.
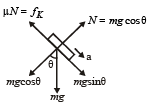
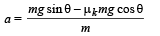
∴ aA = g sin θ – µk,A g cos θ ... (i)
and aB = g sin θ – µk,B g cos θ ... (ii)
Putting values we get

Let aAB is relative acceleration of A w.r.t. B. Then
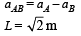
[where L is the relative distance between A and B]
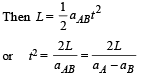
Putting values we get, t2 = 4 or t = 2s.
Distance moved by B during that time is given by
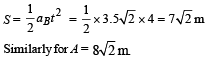
Q.11. A circular disc with a groove along its diameter is placed horizontally on a rough surface. A block of mass 1 kg is placed as shown. The co-efficient of friction between the block and all surfaces of groove and horizontal surface in contact is μ = 2/5. The disc has an acceleration of 25 m/s2 towards left. Find the acceleration of the block with respect to disc. (2006 - 6M)
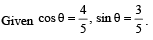
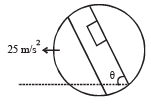
Ans. 10 m/s2
Solution. Applying pseudo force ma and resolving it.
Applying Fnet = mar
ma cos θ – (f1 + f2) = mar
ma cos θ – µN1 –µN2 = mar
ma cos θ – µma sin θ – µ mg = mar
⇒ ar = a cos θ – µa sin θ – µg
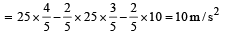
|
481 docs|964 tests
|
















