JEE Advanced (Subjective Type Questions): Work, Energy & Power | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. A bullet is fired from a rifle. If the rifle recoils freely, determine whether the kinetic energy of the rifle is greater than, equal or less than that of the bullet. (1978)

Ans. Less than

Solution.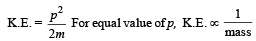 

Q.2. 

A spring of force constant k is cut into three equal parts.

What is force constant of each part?

Ans. 3 times

Solution. KEYCONCEPT : For a spring, (spring constant) × (length) = Constant If length is made one third, the spring constant becomes three times.

Q.3. A 20 gm bullet pierces through a plate of mass M1 = 1 kg and then comes to rest inside a second plate of mass M2 = 2.98 kg. as shown. It is found that the two plates initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between M1 and M2. Neglect any loss of material of the plates due to the action of the  bullet. (1979)

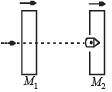
Ans. 25%

Solution. Let v be the velocity of bullet before striking A. Applying conservation of linear momentum for the system of bullet and plate A, we get 0.02v = 0.02 v₁ + 1 × v₂

_{Again applying conservation of linear momentum for collision at B.} 

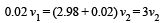
From (i) and (ii)

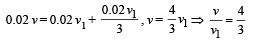
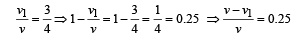
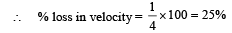
Q.4. When a ball is thrown up, the magnitude of its momentum decreases and then increases. Does this violate the conservation of momentum principle?

Ans. No

Solution. No. An external force, the gravitational pull of earth, is acting on the ball which is responsible for the change in momentum.

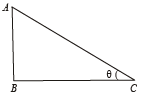
Q.5. In the figures (a) and (b) AC, DG and GF are fixed inclined planes, BC = EF = x and AB = DE = y. A small block of mass M is released from the point A. It slides down AC and reaches C with a speed V_c. The same block is released from rest from the point D. It slides down DGF and reaches the point F with speed VF. The coefficients of kinetic frictions between the block and both the surface AC and DGF are m. (1980) Calculate V_C and V_F.

Ans. 

Solution. K.E. at C = Loss in P.E. – Work done by friction.

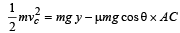
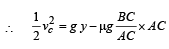
= gy -µgx

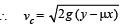
K.E. at F = loss in P.E. – Work done by friction

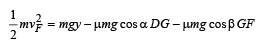
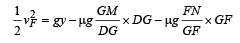
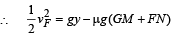
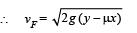
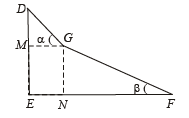
Note : The result does not depend on the angles a and b. It only depends on the values of x and y.

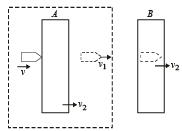
Q.6. Two block s A an d B a re connected to each other by a string and a spring ; the string passes over a frictionless pulley as shown in the figure. Block B slides over the horizontal top  surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed.

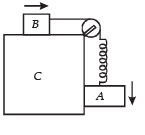
The coefficient of friction between the surfaces of blocks is 0.2. Force constant of the spring is 1960 newtons/m. If mass of block A is  2 Kg., calculate the mass of block B and the energy stored in the spring. (1982 - 5 Marks)

Ans. 10 kg, 0.098 J

Solution. 

Since the two blocks A and B are moving with constant velocity, therefore, the net force acting on A is zero and the net force acting on B will be zero. Since the spring is loaded, it will be in a deformed state. Let the extension of the spring be x.

The forces are drawn.

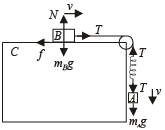
Note : There will be no friction force between block A and C ∴ f = µN. Her e t h ere is no normal reaction on A (because A is not pushing C)

 Applying F_net = ma on A, we get

m_Ag – T = m_A × 0

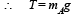
Applying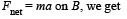

T – f = m_B × 0

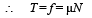
= µm_Bg ... (ii)

From (i) and (ii)

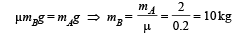
Here the force acting on the spring is the tension (equal to restoring force)

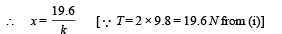
The P.E. stored in spring is given by

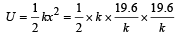
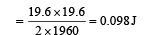
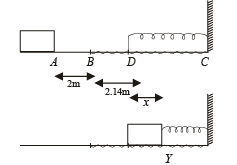
Q.7. A 0.5 kg block slides from the point A (see Fig)  on a horizontal track with an initial speed of 3 m/s towards a weightless horizontal spring of length 1 m and force constant  2 Newton/ m. The part AB of the  track  is frictionless and the part  BC has the coefficients of static and kinetic friction as 0.22 and 0 2 respectively. If the distances AB  and BD are 2 m and 2.14 m respectively, find the total distance  through which the block moves before it comes to rest completely. (Take g = 10m / s²) (1983 - 7  Marks)

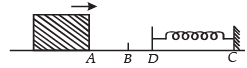
Ans. 4.24 m

Solution. K.E. of block = work against friction + P.E. of spring

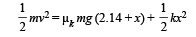
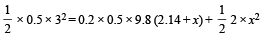
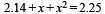
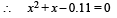
On solving, we get x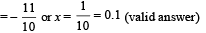 

Here the body stops momentarily.

Restoring force at Y = kx = 2 × 0.1 = 0.2 N

Frictional force at Y = µ_s mg = 0.22 × 0.5 × 9.8 = 1.078 N

Since frictional force > restoring force, the body will stop here.

∴ The total distance travelled

= AB + BD + DY = 2 + 2.14 + 0.1 = 4.24 m.

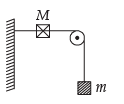
Q.8. A string, with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of 2m from the wall, has a point mass  M = 2kg attached to it at a distance of 1m from the wall. A mass m = 0.5 kg attached at the free end is held at rest so that the string is horizontal between the wall and the pulley and vertical beyond the pulley. What will be the speed with which the mass M will hit the wall when the mass m is released ? (1985 - 6 Marks)

Ans. 3.29 m/s

Solution. 

When mass m is released, since M > m, the mass M will move on a dotted path with O as the centre. There will be decrease in the potential energy of M which will be converted into kinetic energy of M, and increase in potential energy of m.

Decrease in P.E. of M is Mgh 

= 2 × 9.8 × 1 = 19.6 J

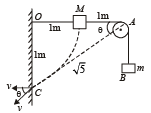
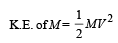
(Let V be the velocity attained by M just before striking the wall)

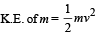
From the figure, by velocity constraint 

v = V cos θ

From ΔOAC,

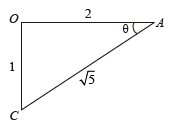
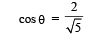
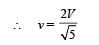
(OC + CA) – OA = height attained by m

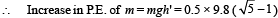
NOTE THIS STEP

By the principle of energy conservation

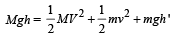
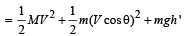
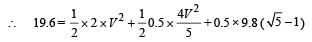
On solving, we get  V = 3.29 m/s

Q.9. A simple pendulum is suspended from a peg on a vertical wall. The pendulum is pulled away from the wall to a horizontal position (see fig.) and released. The 2/√5 ball hits the wall, the coefficient of restitution being 

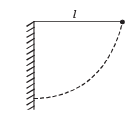
What is the minimum number of collisions after which the amplitude of oscillations becomes less than 60 degrees ?

Ans. 4

Solution. 

The pendulum bob is left from position A. When it is at position C, the angular amplitude is 60°.

In ΔOCM

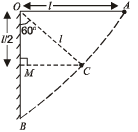
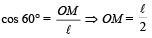
The velocity of bob at B, v_B before first collision is

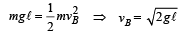
Let after n collisions, the angular amplitude is 60° when the bob again moves towards the wall from C, the velocity v'B before collision is

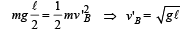
This means that the velocity of the bob should reduce from

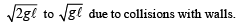
The final velocity after n collisions is √gl

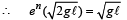
where e is coefficient of restitution.

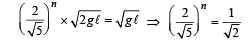
Taking log on both sides we get

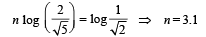
Therefore, number of collisions will be 4.

Q.10.  Two blocks of mass 2 kg and M are at rest on an inclined plane and are separated by a distance of 6.0 m as shown in Figure. The coefficient of friction between each of the blocks and the inclined plane is 0.25. The 2 kg block is given a velocity of 10.0 m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0 m/s when it reaches its initial position. The other block M after the collision moves 0.5 m up and comes to rest. Calculate the coefficient of restitution between the blocks and  the mass of the block M. [Take sin q » tan q = 0.05 and g = 10m / s 2 . ] (1999 - 10 Marks)

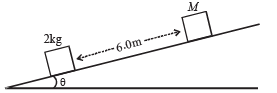
Ans.  0.84; 15.02 kg.

Solution. Fr om A to B. 

u = 10 m/s    (given)

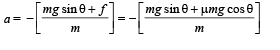
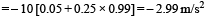
v = ?

s = 6 m

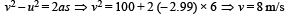
⇒ The velocity of mass m just before collision is 8 m/s.

The velocity of mass M just before collision is 0 m/s (given).

AFTER COLLISION

Let v₁ be the velocity of mass m after collision and v₂ be the velocity of mass M after collision. Body of mass M moving from B to C and coming to rest. 

u = v₂

 v = 0

 a = – 2.99 m/s²

 (same as of previous case because all other things are same except mass. a is independent of mass) s = 0.5

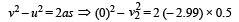
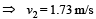
Body of mass m moving from B to A after collision

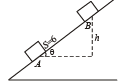
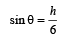
h = 6 sin θ = 6 × 0.05      

u = v₁ 

v = + 1m/s

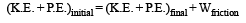
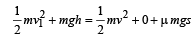
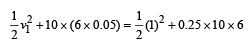
v₁ = – 5 m/s

Coefficient of restitution

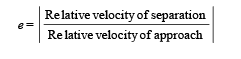
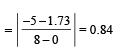
On applying conservation of linear momentum before and after collision, we get 

2 × 8 + M × 0 = 2 × (– 5) + M (1.73)

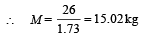
Q.11. A spherical ball of mass m is kept at the highest point in the space between two fixed, concentric spheres A and B (see figure). The smaller sphere A has a radius R and the space between the two spheres has a width d. The ball has a diameter very slightly less than d. All surfaces are frictionless. The ball is given a gentle push (towards the right in the figure). The angle made by the radius vector of the ball with the upward vertical is denoted by θ (shown in the figure). (2002 - 5 Marks)

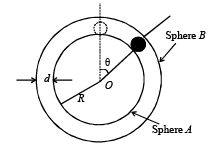
(a) Express the total normal reaction force exerted by the sphere on the ball as a function of angle θ.

 (b) Let N_A and N_B denote the magnitudes of the normal reaction forces on the ball exerted by the sphere A and B, respectively. Sketch the variations of N_A and N_B as functions of cos q in the range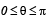 

 by drawing two separate graphs in your answer book, taking cos θ on the horizontal axes.

Ans.  (a)  N_A = mg (3cosθ – 2)

Solution. The ball is moving in a circular motion. The necessary centripetal force is provided by (mg cosθ – N). Therefore,

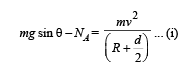
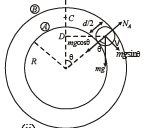
According to energy conservation

From (i) and (ii) 

N_A = mg (3 cos θ – 2) ... (iii

The above equation shows that as q increases NA decreases.

At a particular value of q , N_A will become zero and the ball will lose contact with sphere A. This condition can be found by putting N_A = 0 in eq. (iii)

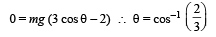
The graph between N_A and cosθ From equation (iii) when q = 0, N_A = mg.

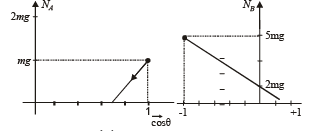
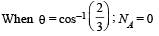
The graph is a straight line as shown.

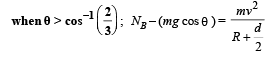
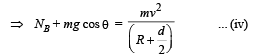
Using energy conservation

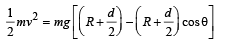
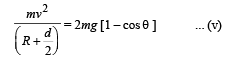
From (iv) and (v), we get

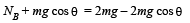
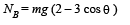
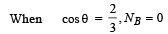
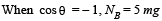
Therefore the graph is as shown.