Subjective Type Questions: Momentum and Impulse | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. A body of mass m moving with velocity V in the X-direction collides with another body of mass M moving in Y-direction with velocity v. They coalesce into one body during collision. Calculate : (1978)
(i) the direction and magnitude of the momentum of the final body.
(ii) the fraction of initial kinetic energy transformed into heat during the collision in terms of the two masses.
Ans.


Solution. Let V' be the velocity of the final body after collision.
Suppose, V' makes an angle θ with x-direction.
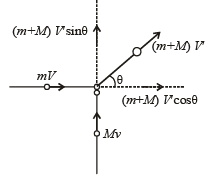
(i) Applyin g con ser vation of linear momen tum in X direction
(m + M) V' cos θ = mV ... (i)
Applying conservation of linear momentum in Y direction
(m + M) V' sin θ = Mv ... (ii)
Dividing equation (i) and (ii)
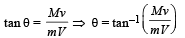
This gives the direction of the momentum of the final body.
Squaring and adding (i) and (ii), we get
(m + M)2 V'2 cos2 θ + (m + M)2 V'2 sin2θ
= m2V2 + M2v2
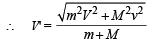
Thus the magnitude of the momentum of the final body
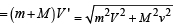
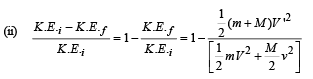
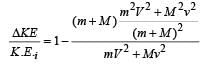
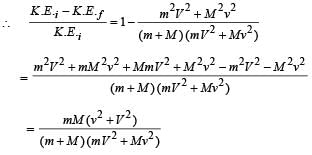
Q.2. Three particles A, B and C of equal mass move with equal speed V along the medians of an equilateral triangle as shown in figure. They collide at the centroid G of the triangle. After the collision, A comes to rest, B retraces its path with the speed V. What is the velocity of C ? (1982 - 2 Marks)
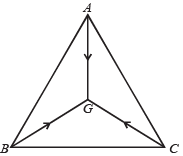
Ans. V, opposite direction to the retraced velocity of B
Solution.
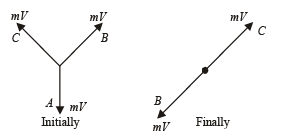
Initially By symmetry, the momentum of the system is zero.
Finally The momentum of the system should be zero.
∴ mV = mV' ⇒ V' = V
The velocity of C is V and is in opposite direction to the retraced velocity of B as shown in the figure.
Q.3. Two bodies A and B of masses m and 2 m respectively are placed on a smooth floor. They are connected by a spring. A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A as shown in Fig.

At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0; and (ii) the spring constant. (1984- 6 Marks)
Ans. 
Solution. Since the collision between C and A is elastic and their masses are equal and A was initially at rest, therefore the result of collision will be that C will come to rest and A will initially start moving with a velocity v0. But since A is connected to B with a spring, the spring will get compressed.
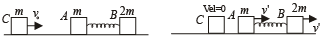
At t = t0, the velocities of A and B become same.
Applying energy conservation;
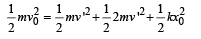
where x0 is the compression in the spring at t = t0
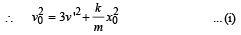
Applying momentum conservation, we get

From (i) and (ii)
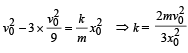
Q.4. A ball of mass 100 gm is projected vertically upwards from the ground with a velocity of 49 m/sec. At the same time another identical ball is dropped from a height of 98 m to fall freely along the same path as that followed by the first ball. After some time the two balls collide and stick together and finally fall to the ground. Find the time of flight of the masses. (1985 - 8 Marks)
Ans. 6.53 sec
Solution. For the ball thrown up
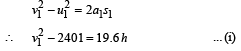
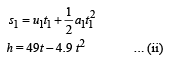
For the ball dropped from height
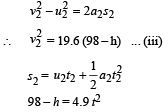
From (ii) and (iv)
98 – (49t – 4.9t2) = 4.9t2 ∴ 98 – 49t = 0
∴ t = 2 sec
∴ h = 49 × 2 – 4.9 × 22 = 78.4 m (from (ii))
Substituting this value of h in (i) and (ii), we get

Note : At point C where the two bodies collide, thereafter both bodies stick and behave as a single body.
Thus, we apply conservation of linear momentum, which gives
For the combined body
u = 4.9 m/s; s1 = – 78.4; a1 = – 9.8 m/s2; t = ?
Total time = 4.53 + 2 = 6.53 sec.
Q.5. A bullet of mass M is fired with a velocity 50 m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embedded in the bob. After the collision, the string moves through an angle of 120°. Find
(i) the angle θ ;
(ii) the vertical an d horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g =10 m /s2
Ans. 37°, 122.6 m, 46 m
Solution. (i) In Δ AQR

u = 50 m/s (Given)
At the highest point P, the velocity of the bullet = u cos θ

Applying conservation of linear momentum at the highest point
M (u cos θ) + 3M × 0 = (M + 3M) v
Applying energy conservation principle for P and R K.E. of the bullet-mass system at P = P.E. of the bullet-mass system at R
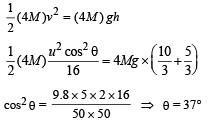
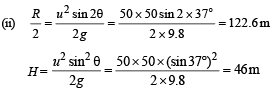
Q.6. A block ‘A’ of mass 2m is placed on another block ‘B’ of mass 4m which in turn is placed on a fixed table. The two blocks have a same length 4d and they are placed as shown in fig. The coefficient of friction (both static and kinetic) between the block ‘B’ and table is μ . There is no friction between the two blocks. A small object of mass m moving horizontally along a line passing through the centre of mass (cm.) of the block B and perpendicular to its face with a speed v collides elastically with the block B at a height d above the table. (1991 - 4 + 4 Marks)
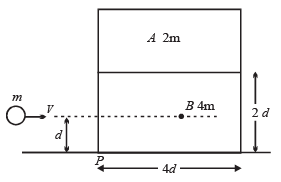
(a) What is the minimum value of v (call it v0) required to make the block A topple ?
(b) If v = 2v0, find the distance (from the point P in the figure) at which the mass m falls on the table after collision. (Ignore the role of friction during the collision).
Ans. 
Solution. KEY CONCEPT : Since the collision is elastic in nature applying conservation of linear momentum and conservation of kinetic energy
mv = (4m) u + mv'
where u is the velocity of mass 4m after collision and v' is the velocity of mass 2m
⇒ v' = v – 4u ... (i)
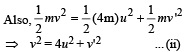

From (i) to (ii)
Block B starts moving but the block A remains at rest as there is no friction between A and B.
For block A to topple, block B should move a distance 2d.
Let the retardation produced in B due to friction force between B and the table be a
F = μN ⇒ (4 m)a = μ (6 mg) ⇒ a = 1.5 µg
For the motion of B,
For elastic collision between two bodies
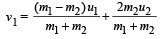


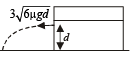
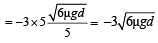
Note : The negative sign shows that the mass m rebounds.
It then follows a projectile motion.
Considering the vertical direction motion of this projectile.
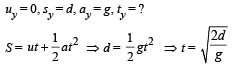
The horizontal distance travelled by mass m during this time t
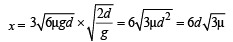
Q.7. A cart is moving along + x direction with a velocity of 4 m/s.
A person on the cart throws a stone with a velocity of 6 m/s relative to himself. In the frame of reference of the cart the stone is thrown in y-z plane making an angle of 30° with vertical z-axis. At the highest point of its trajectory, the stone hits an object of equal mass hung vertically from the branch of a tree by means of a string of length L. A completely inelastic collision occurs, in which the stone gets embedded in the object. Determine : (1997 - 5 Marks)
(i) The speed of the combined mass immediately after the collision with respect to an observer on the ground,
(ii) The length L of the string such that the tension in the string becomes zero when the string becomes horizontal during the subsequent motion of the combined mass.
Ans. 2.5 m/s, 0.318 m
Solution. When the stone reaches the point Q, the component of velocity in the + Z direction (v cos θ) becomes zero due to the gravitational force in the – Z direction.
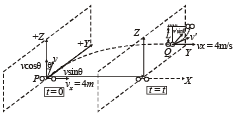
The stone has two velocities at Q
vx in the + X direction (4 m/s)
v sin θ in the + Y direction (6 sin 30° = 3 m/s)
The resultant velocity of the stone
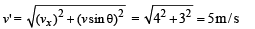
(i) Applying conservation of linear momentum at Q for collision with a mass of equal magnitude m × 5 = 2m × v
Note : Since, the collision is completely inelastic the two masses will stick together. v is the velocity of the two masses just after collision.]
∴ v = 2.5 m/s
(ii) When the string is undergoing circular motion, at any arbitrary position
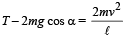
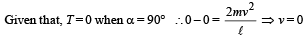
⇒ Velocity is zero when α = 90°, i.e., in the horizontal position.

Applying energy conservation from Q to M, we ge

Q.8. A car P is moving with a uniform speed of 5√3 m/s towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity 100 m/s at an angle 30o with the horizontal. The first cannon ball hits the stationary carriage after a time to and sticks to it. Determine to.
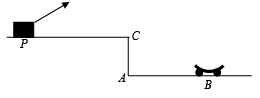
At to, the second cannon ball is fired. Assume that the resistive force between the rails and the carriage is constant and ignore the vertical motion of the carriage throughout. If the second ball also hits and sticks to the carriage, what will be the horizontal velocity of the carriage just after the second impact?
Ans. 12 s, 15.75 m/s
Solution. Consider the vertical motion of the cannon ball
uy = + 100 sin 30°
sy = – 120 m
ay = – 10 m/s2
t = t0
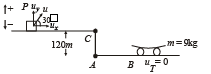

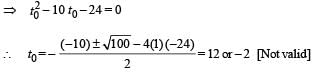
∴ t0 = 12 sec.
The horizontal velocity of the cannon ball remains the same
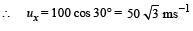
∴ Applying conser vation of linear momentum to the cannon ball-trolley system in horizontal direction. If m is the mass of cannon ball and M is the mass of the trolley then,
mux + M × 0 = (m + M) vx
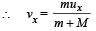
where vx is the velocity of the cannon ball-trolley system.
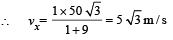
The second ball was projected after 12 second. Horizontal distance covered by the car P

Since the second ball also struck the trolley, Therefore, in time 12 seconds, the trolley covers a distance of 60√3m.
For trolley after 12 seconds;
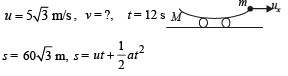
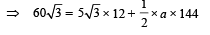
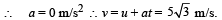
To find the final velocity of the carriage after the second impact we again apply conservation of linear momentum in the horizontal direction

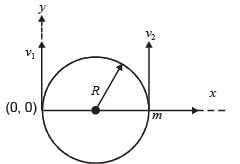
Q.9. A particle of mass m, moving in a circular path of radius R with a constant speed v2 is located at point (2R, 0) at time t = 0 and a man starts moving with a velocity v1 along the +ve y-axis from origin at time t = 0. Calculate the linear momentum of the particle w.r.t. the man as a function of time. (2003 - 2 Marks)
Ans. 
Solution.

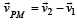

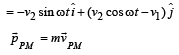

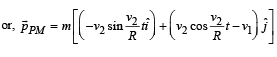
|
347 docs|185 tests
|
FAQs on Subjective Type Questions: Momentum and Impulse - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is momentum and how is it related to impulse? |  |
| 2. How is momentum conserved in a collision? |  |
| 3. What is the difference between elastic and inelastic collisions? |  |
| 4. How does impulse affect the motion of an object? |  |
| 5. How can the concept of momentum and impulse be applied in real-life situations? |  |
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|

















