Formation of Compounds with Congruent & Incongruent Melting Point | Physical Chemistry PDF Download
Solid Solution
A solid solution is a uniform mixture of two crystalline solids that share a common crystal lattice. Solid solutions often consist of two or more types of atoms or molecules that share a crystal lattice, as in certain metal alloys. Solvent is the element or compound that is present in the greatest amount. Solute is used to denote an element or compound present in a minor concentration. The solute may incorporate into the solvent crystal lattice substitutionally, by replacing a solvent particle in the lattice, or interstitially, by fitting into the space between solvent particles. Both of these types of solid solution affect the properties of the material by distorting the crystal lattice and disrupting the physical and electrical homogeneity of the solvent material.
System in which two components form a stable compound
There are other type of systems in which component (metals, organics compounds at inorganic salts) enter into chemical combination giving rise to one or more compounds.
Such type of two-compounds system are of two kinds:
- Two components form a compound with congruent melting point.
Examples are: Zn-Mg, Al-Mg, Hg-Tl, Au-Sn, FeCl3-H2O etc. - Two compounds from a compound with incongruent melting point.
Examples are: Picric acid-benzene, Au-Sb, Na-K, NaCl, H2O, Na2SO4-H2O etc.
Formation of Compounds with Congruent Melting Point
“A compound is said to have a congruent melting point when it melts sharply at a constant temperature into a liquid of the same compositions as that of solid form from which it is derived.” The temperature is called congruent melting point. Suppose A and B are two components and AB is the compound formed by the chemical combination.
The phase diagram is shown in figure:
It has three different solid phases A, B and compound AB and there are three fusion curves AC, BE and CDE. Along the curve AC, the solid A is in equilibrium with the solution of the component B in A. Point A represents the freezing point of pure A. By gradual addition of B to A, the freezing point of A is lowered along the curve AC. Therefore, the number of phases along AC is two.
Applying the condensed phase rule of the system, we get
F = C – P + 1 = 2 – 2 + 1 = 1
Thus the system is monovariant. Only the composition varies along AC.
Similarly B is the freezing point of pure component B. Point D represent the congruent point of compound AB since solid and liquid phases have same composition on it and bicomponent system reduces to unicomponent system at this point. Point D is a nonvariant point since it indicates a definite temperature. In this phase diagram this temperature is higher than the melting points of either A or B although congruent temperature may be higher, lower or in between the melting point of A and B. There are two eutectic point C and E in the diagram. At point C, solid A and solid AB are in equilibrium with liquid phase whereas at E, solid B, solid compound AB are in equilibrium with liquid phase.
It has been observed that at a temperature ‘t’ two composition x1 and x’ of liquid phase are in equilibrium with solid AB or AB exhibits two solubilities at one temperature (t). In phase diagram it may be explained as follows.
A line DD’ bisects the curve in two equal parts. Left hand part represents bicomponent system of A and AB and right hand part represents bicomponent system of Band AB. Curve DC represents the addition of A in a solid AB, whereas DE represents addition of B into solid AB.
Zn-Mg System
It is an example of a two component system in which two metals form a compound having Mg(Zn)2 having congruent melting point. Melting point of pure Zn is 420°C (point A), and that of pure Mg is 650°C (point B) whereas m.p. of compound Mg(Zn)2 is 590°C (point D) which is in between the melting point of two metals. This system has four phases i.e. solid Zn, solid Mg solid compound Mg(Zn)2 and melt of Zn and Mg.
Important features of the phase diagram
- Point A: It represents the m.p. of pure Zn (420°C)
- Curve AC: When Mg is added to Zn gradually the m.p. of Zn is lowered along the curve AC. Along this curve solid Zn is in equilibrium with melt (liquid). Thus there two phases along this curve and on applying the condensed phase rule F = C – P + 1 = 2 – 2 + 1 = 1 we see that it is a monovariant system. It means only the composition varies along this curve.
- Point B: This represents the melting point of pure Mg (650°C)
- Curve BE: When Zn is added to Mg gradually, m.p. of Mg is lowered along the curve BE. Along the curve BE solid Mg is in equilibrium with melt (liquid). Again this is also a monovarient curve having one degree of freedom.
- Curve DC: This curve represents the freezing point curve of solid Mg(Zn)2 when Zn is added, the m.p. of compound Mg(Zn)2 lowers along this curve.
- Curve DC: This curve represents the freezing point curve of solid Mg(Zn)2 when Zn is added, the m.p. of compound Mg(Zn)2 lowers along this curve.
- Curve DE: This curve represents the melting point curve of Mg(Zn)2 when Mg is added in it.
- Point D: At this point, the liquid and solid have the same composition i.e. Mg(Zn)2. Thus point D is the congruent point and temperature (590°C) corresponds to this point is known as congruent melting point of Mg(Zn)2.
- Point C: Two curve AC and DC intersect at point C. Three phases i.e. solid Zn, compound Mg(Zn)2 and melt are in equilibrium at this point.
Thus, on applying phase rule F = C – P + 1 = 2 – 3 + 1 = 0 we see that point C is non variant point C is known as eutectic point. - Point E: This is the point where curves DE and BE intersect. Here also three phases i.e. solid Mg, compound Mg(Zn)2 and melt are in equilibrium at this point. Again it is invariant and known as eutectic point.
- Cooling: When liquid melt is cooled at point X, it follows the path xy and Mg(Zn)2 seperates out at y and two phases i.e. solid Mg(Zn)2 and liquid are in equilibrium and the degree of freedom is one. On further cooling curve follows the path yC and at C, solid Zn also separates out. Thus there will be three phases at point C. These phases are solid Zn, solid Mg(Zn)2 and melt. Therefore C is monovariant.
Formation of compounds with incongruent melting point
In many two components systems, components form a compound with incongruent melting point. The compound formed is so unstable that it decomposes instead of melting to form a new solid phase and a solution of the solid at a temperature which is well below its melting point. Such a compound is said to have incongruent melting point. Decomposition of this compound is termed as the transition or meritectic or peritectic reaction.
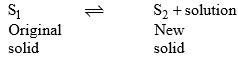
Incongruent melting point is called meritectic or peritectic temperature. In this process three phases i.e. two solids and one liquid are present so it is nonvariant system.
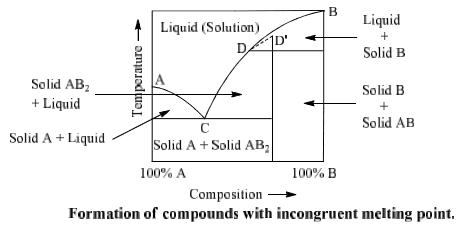
Suppose A and B are two components which form a compound AB2 on combination. Point A and B represent the melting points of pure A and pure B respectively whereas point D represents the incongruent melting point for AB2. Curves AC and BD represent the fusion curves of component. A and B respectively. Component A and liquid are in equilibrium on curve AC of compound AB2 on which AB2 and liquid are in equilibrium.
Compound AB2 dissociates at D as follows: 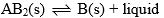
Component B and liquid are in equilibrium on curve BD. Curve CD is the fusion curve Similarly point C is nonvariant at which solid A, solid AB2 and liquid are in equilibrium (F = 0). This point is called eutectic point. Curve CD can be extended upto ‘D’. Point D is a called submerged maxima since it is not observed in practice. Picric acid-Benzene, Gold-Antimony, Sodium-Potassium, Sodium sulphate-water, sodium chloride-water are some examples of such type of system.
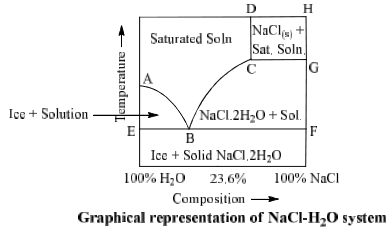
NaCl-H2O System
Phase diagram of NaCl—H2O system is shown in fig.
NaCl.2H2O ⇌ NaCl + solution
Area ABCD consists of saturated solution of NaCl and area ABE has two phases, viz., ice and saturated solution. Solid NaCl + saturated solution are found in area CDHG and area CBFG have two solid phases NaCl.2H2O + saturated solution.
Ferric Chloride-Water System
The phase diagram has four maxima corresponding to the formation of four hydrates. Point C (37°C). E(32.5°C) and I(78.5°C) represent the congruent melting point of dodeca, hepta, penta and tetra hydrates respectively. The congruent melting point of a salt hydrate is also known as the dyestectic point.
Copper sulphate water vapour system
Phase diagram of this system in shown in figure:
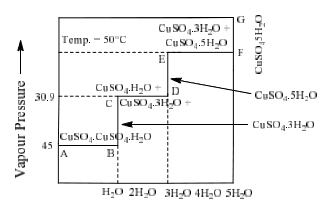
|
90 videos|144 docs|67 tests
|
FAQs on Formation of Compounds with Congruent & Incongruent Melting Point - Physical Chemistry
| 1. What is the difference between compounds with congruent and incongruent melting points? |  |
| 2. How are compounds with congruent melting points formed? |  |
| 3. What factors influence the formation of compounds with incongruent melting points? |  |
| 4. Can the formation of compounds with incongruent melting points be controlled? |  |
| 5. Are compounds with incongruent melting points less stable than compounds with congruent melting points? |  |






















