Ex-2.2 Polynomials, Class 10, Maths RD Sharma Solutions PDF Download
Q.1: Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and coefficients in each of the following cases:
(i) f(x) = 2x3 + x2 – 5x + 2;1/2,1,−2
(ii) g(x) = x3 – 4x2 + 5x – 2;2,1,1
Sol: (i) f(x) = 2x3 + x2 – 5x + 2;1/2,1,−2
(a) By putting x = 1/2 in the above equation, we will get
f(1/2) = 2(1/2)3 + (1/2)2 – 5(1/2) + 2
= f(1/2) = 2(1/8) + 1/4 – 5/2 + 2
= f(1/2) = 1/4 + 1/4 – 5/2 + 2 = 0
(b) By putting x = 1 in the above equation, we will get
f(1) = 2(1)3 + (1)2 – 5(1) + 2
= 2 + 1 – 5 + 2 = 0
(c) By putting x = -2 in the above equation, we will get
f(−2) = 2(−2)3 + (−2)2 – 5(−2) + 2
= -16 + 4 + 10 + 2 = -16 + 16 = 0
Now,
Sum of zeroes = α + β + γ = −b/a
⇒ 1/2 + 1−2 = −1/2
−1/2 = −1/2
Product of the zeroes = αβ + βγ + αγ = c/a
1/2×1 + 1×(−2) + (−2)×1/2 = −5/2
1/2 – 2 – 1 = −5/2
−5/2 = −5/2
Hence, verified.
(ii) g(x) = x3 – 4x2 + 5x – 2;2,1,1
(a) By putting x = 2 in the given equation, we will get
g(2) = (2)3 – 4(2)2 + 5(2) – 2
= 8 – 16 + 10 – 2 = 18 – 18 = 0
(b) By putting x = 1 in the given equation, we will get
g(1) = (1)3 – 4(1)2 + 5(1) – 2
= 1 – 4 + 5 – 2 = 0
Now,
Sum of zeroes = α + β + γ = −b/a
⇒ 2 + 1 + 1 = −(−4)
4 = 4
Product of the zeroes = αβ + βγ + αγ = c/a
2×1 + 1×1 + 1×2 = 5
2 + 1 + 2 = 5
5 = 5
αβγ = – (−2)
2×1×1 = 2
2 = 2
Hence, verified.
Q.2: Find a cubic polynomial with the sum, sum of the product of its zeroes is taken two at a time, and product of its zeroes as 3, -1 and -3 respectively.
Sol: Any cubic polynomial is of the form ax3 + bx2 + cx + d :
= x3 – (sum of the zeroes) x2 + (sum of the products of its zeroes) x – (product of the zeroes)
= x3 – 3x2 + (−1)x + (−3)
= k[x3 – 3x2 – x – 3]
k is any non-zero real numbers.
Q.3: If the zeroes of the polynomial f(x) = 2x3 – 15x2 + 37x – 30, find them.
Sol: Let, α = a – d,β = a and γ = a + d be the zeroes of the polynomial.
f(x) = 2x3 – 15x2 + 37x – 30
α + β + γ = – (−15/2) = 15/2
αβγ = – (−30/2) = 15
a – d + a + a + d = 15/2 and a(a – d)(a + d) = 15
So, 3a = 15/2
a = 5/2
And, a(a2 + d2) = 15
d2 = 1/4
d = 1/2
Therefore, α = 5/2 – 1/2 = 4/2 = 2
β = 5/2
γ = 5/2 + 1/2 = 3
Q.4: Find the condition that the zeroes of the polynomial f(x) = x3 + 3px2 + 3qx + r may be in A.P.
Sol: f(x) = x3 + 3px2 + 3qx + r
Let, a – d, a, a + d be the zeroes of the polynomial.
Then,
The sum of zeroes = −b/a
a + a – d + a + d = -3p
3a = -3p
a = -p
Since, a is the zero of the polynomial f(x),
Therefore, f(a) = 0
f(a) = a3 + 3pa2 + 3qa + r = 0
Therefore, f(a) = 0
= ⇒ a3 + 3pa2 + 3qa + r = 0
= ⇒ (−p)3 + 3p(−p)2 + 3q(−p) + r = 0
= −p3 + 3p3 – pq + r = 0
= 2p3 – pq + r = 0
Q.5: If zeroes of the polynomial f(x) = ax3 + 3bx2 + 3cx + d are tin A.P., prove that 2b3 – 3abc + a2d = 0.
Sol: f(x) = x3 + 3px2 + 3qx + r
Let, a – d, a, a + d be the zeroes of the polynomial.
Then,
The sum of zeroes = −b/a
a + a – d + a + d = −3b/a
⇒ 3a = −3b/a
⇒ a = −3b/3a = −b/a
Since,f(a) = 0
⇒ a(a2) + 3b(a)2 + 3c(a) + d = 0
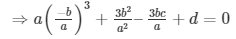
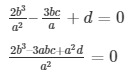
2b3 – 3abc + a2d = 0
Q.6: If the zeroes of the polynomial f(x) = x3 – 12x2 + 39x + k are in A.P., find the value of k.
Sol: f(x) = x3 – 12x2 + 39x + k
Let, a-d, a, a + d be the zeroes of the polynomial f(x).
The sum of the zeroes = 12
3a = 12
a = 4
Now,
f(a) = 0
f(a) = a3 – 12a2 + 39a + k
f(4) = 43 – 12(4)2 + 39(4) + k = 0
64 – 192 + 156 + k = 0
k = -28
FAQs on Ex-2.2 Polynomials, Class 10, Maths RD Sharma Solutions
| 1. What are polynomials? |  |
| 2. What is the degree of a polynomial? |  |
| 3. How can we add or subtract polynomials? |  |
| 4. What is the Zero of a polynomial? |  |
| 5. How can we multiply polynomials? |  |



















