Ex-4.2 Triangles, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Exercise 4.2
Q.1: In a Δ ABC, D and E are points on the sides AB and AC respectively such that DE ∥ BC.
1.) If AD = 6 cm, DB = 9 cm and AE = 8 cm, Find AC.
2.) If ADDB = 34 and AC = 15 cm, Find AE.
3.) If ADDB = 23 and AC = 18 cm, Find AE.
4.) If AD = 4 cm, AE = 8 cm, DB = x – 4 cm and EC = 3x – 19, find x.
5.) If AD = 8 cm, AB = 12 cm and AE = 12 cm, find CE.
6.) If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
7.) If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
8.) If ADBD = 45 and EC = 2.5 cm, Find AE.
9.) If AD = x cm, DB = x – 2 cm, AE = x + 2 cm, and EC = x – 1 cm, find the value of x.
10.) If AD = 8x – 7 cm, DB = 5x – 3 cm, AE = 4x – 3 cm, and EC = (3x – 1) cm, Find the value of x.
11.) If AD = 4x – 3, AE = 8x – 7, BD = 3x – 1, and CE = 5x – 3, find the value of x.
12.) If AD = 2.5 cm, BD = 3.0 cm, and AE = 3.75 cm, find the length of AC.
Sol: 1) It is given that Δ ABC AND DE ∥ BC
We have to find AC,
Since, AD = 6 cm,
DB = 9 cm and AE = 15 cm.
AB = 15 cm.
So, AD/BD = AE/CE (using Thales Theorem)
Then, 6/9 = 8/x
6x = 72 cm
x = 72/6 cm
x = 12 cm
Hence, AC = 12 + 8 = 20.
2) It is given that AD/BD = 3/4 and AC = 15 cm
We have to find out AE,
Let, AE = x
So, AD/BD = AE/CE (using Thales Theorem)
Then, 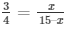
45 – 3x = 4x
-3x – 4x = – 45
7x = 45
x = 45/7
x = 6.43 cm
3) It is given that AD/BD = 2/3 and AC = 18 cm
We have to find out AE,
Let, AE = x and CE = 18 – x
So, AD/BD = AE/CE (using Thales Theorem)
Then, 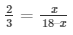
3x = 36 – 2x
5x = 36 cm
X = 36/5 cm
X = 7.2 cm
Hence, AE = 7.2 cm
4) It is given that AD = 4 cm, AE = 8 cm, DB = x – 4 and EC = 3x – 19
We have to find x,
So, AD/BD = AE/CE (using Thales Theorem)
Then, 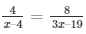
4(3x – 19) = 8(x – 4)
12x – 76 = 8(x – 4)
12x – 8x = – 32 + 76
4x = 44 cm
X = 11 cm
5) It is given that AD = 8 cm, AB = 12 cm, and AE = 12 cm.
We have to find CE,
So, AD/BD = AE/CE (using Thales Theorem)
Then, 8/4 = 12/CE
8CE = 4 X 12 cm
CE = (4 X 12)/8 cm
CE = 48/8 cm
CE = 6 cm
6) It is given that AD = 4 cm, DB = 4.5 cm, AE = 8 cm
We have to find out AC
So, AD/BD = AE/CE (using Thales Theorem)
Then, 4/4.5 = 8/AC
AC = 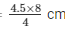
AC = 9 cm
7) It is given that AD = 2 cm, AB = 6 cm, and AC = 9 cm
We have to find out AE
DB = 6 – 2 = 4 cm
So, AD/BD = AE/CE (using Thales Theorem)
Then, 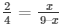
4x = 18 – 2x
6x = 18
X = 3 cm
8) It is given that AD/BD = 4/5 and EC = 2.5 cm
We have to find out AE
So, AD/BD = AE/CE (using Thales Theorem)
Then, 4/5 = AE/2.5
AE = 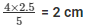
9) It is given that AD = x, DB = x – 2, AE = x + 2 and EC = x – 1
We have to find the value of x
So, AD/BD = AE/CE (using Thales Theorem)
Then, 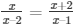
X(x – 1) = (x – 2)(x + 2)
x2 – x – x2 + 4 = 0
x = 4
10) It is given that AD = 8x – 7, DB = 5x – 3, AER = 4x – 3 and EC = 3x -1
We have to find the value of x
So, AD/BD = AE/CE (using Thales Theorem)
Then, 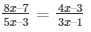
(8x – 7)(3x – 1) = (5x – 3)(4x – 3)
24x2 – 29x + 7 = 20x2 – 27x + 9
4x2 – 2x – 2 = 0
2(2x2 – x – 1) = 0
2x2 – x – 1 = 0
2x2 – 2x + x – 1 = 0
2x(x – 1) + 1(x – 1) = 0
(x – 1)(2x + 1) = 0
X = 1 or x = -1/2
Since the side of triangle can never be negative
Therefore, x = 1.
11) It is given that AD = 4x – 3, BD = 3x – 1, AE = 8x – 7 and EC = 5x – 3
For finding the value of x
So, AD/BD = AE/CE (using Thales Theorem)
Then, 
(4x – 3)(5x – 3) = (3x – 1)(8x – 7)
4x(5x – 3) -3(5x – 3) = 3x(8x – 7) -1(8x – 7)
20x2 – 12x – 15x + 9 = 24x2 – 29x + 7
20x2 -27x + 9 = 242 -29x + 7
Then,
-4x2 + 2x + 2 = 0
4x2 – 2x – 2 = 0
4x2 – 4x + 2x – 2 = 0
4x(x – 1) + 2(x – 1) = 0
(4x + 2)(x – 1) = 0
X = 1 or x = -2/4
Since, side of triangle can never be negative
Therefore x = 1
12) It is given that, AD = 2.5 cm, AE = 3.75 cm and BD = 3 cm
So, AD/BD = AE/CE (using Thales Theorem)
Then, 2.5/3 = 3.75/CE
2.5CE = 3.75 x 3
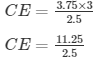
CE = 4.5
Now, AC = 3.75 + 4.5
AC = 8.25 cm.
Q.2) In a Δ ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DE ∥ BC.
1.) AB = 12 cm, AD = 8 cm, AE = 12 cm, and AC = 18 cm.
2.) AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm, and AE = 1.8 cm.
3.) AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm, and AE = 2.8 cm.
4.) AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm, and EC = 5.5 cm.
Sol: 1) It is given that D and R are the points on sides AB and AC.
We have to find that DE ∥ BC.
Acc. To Thales Theorem,
AD/DB = AE/CE
8/4 = 12/6
2 = 2 (LHS = RHS)
Hence, DE ∥ BC.
2) It is given that D and E are the points on sides AB and AC
We need to prove that DE ∥ BC
Acc. To Thales Theorem,
AD/DB = AE/CE
1.4/4.2 = 1.8/5.4
1/3 = 1/3 (RHS)
Hence, DE ∥ BC.
3) It is given that D and E are the points on sides AB and AC.
We need to prove DE ∥ BC.
Acc. To Thales Theorem,
AD/DB = AE/CE
AD = AB – DB = 10.8 – 4.5 = 6.3
And,
EC = AC – AE = 4.8 – 2.8 = 2
Now,
6.34.5 = 2.82.0
Hence, DE ∥ BC.
4) It is given that D and E are the points on sides AB and Ac.
We need to prove that DE ∥ BC.
Acc. To Thales Theorem,
AD/DB = AE/CE
5.7/9.5 = 3.3/5.5
3/5 = 3/5 (LHS = RHS)
Hence, DE ∥ BC.
Q.3) In a Δ ABC, P and Q are the points on sides AB and AC respectively, such that PQ ∥ BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm, and BC = 6 cm, Find AB and PQ.
Sol: It is given that AP = 2.4 cm, AQ = 2 cm, QC = 3 cm, and BC = 6 cm.
We need to find AB and PQ.
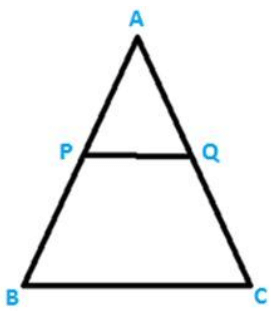
Using Thales Theorem,
AP/PB = AQ/QC
2.4/PB = 2/3
2PB = 2.4 x 3 cm
PB = 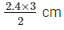
PB = 3.6 cm
Now, AB = AP + PB
AB = 2.4 + 3.6
AB = 6 cm
Since, PQ ∥ BC, AB is transversal, then,
Δ APQ = Δ ABC (by corresponding angles)
Since, PQ ∥ BC, AC is transversal, then,
Δ APQ = Δ ABC (by corresponding angles)
In Δ ABQ and Δ ABC,
∠APQ = ∠ABC
∠AQP = ∠ACB
Therefore, Δ APQ = Δ ABC (angle angle similarity)
Since, the corresponding sides of similar triangles are proportional,
Therefore, AP/AB = PQ/BC = AQ/AC
AP/AB = PQ/BC
2.4/6 = PQ/6
Therefore, PQ = 2.4 cm.
Q.4) In a Δ ABC, D and E are points on AB and AC respectively, such that DE ∥ BC. If AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm, and BC = 5 cm. Find BD and CE.
Sol: It is given that AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BE = 5 cm.
We need to find BD and CE.
Since, DE ∥ BC, AB is transversal, then,
∠APQ = ∠ABC
Since, DE ∥ BC, AC is transversal, then,
∠AED = ∠ACB
In Δ ADE and Δ ABC,
∠ADE = ∠ABC
∠AED = ∠ACB
So, Δ ADE = Δ ABC (angle angle similarity)
Since, the corresponding sides of similar triangles are proportional, then,
Therefore, AD/AB = AE/AC = DE/BC
AD/AB = DE/BC
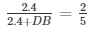
2.4 + DB = 6
DB = 6 – 2.4
DB = 3.6 cm
Similarly, AE/AC = DE/BC
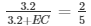
3.2 + EC = 8
EC = 8 – 3.2
EC = 4.8 cm
Therefore, BD = 3.6 cm and CE = 4.8 cm.
Q.5) In figure given below, state PQ ∥ EF.
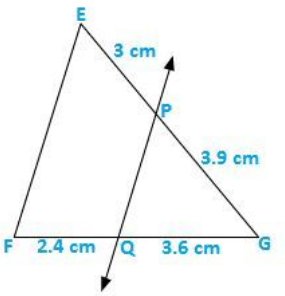
Sol:
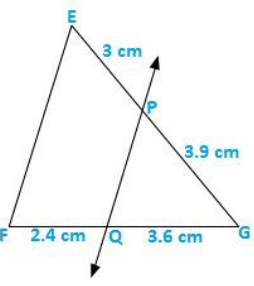
It is given that EP = 3 cm, PG = 3.9 cm, FQ = 3.6 cm and QG = 2.4 cm
We have to check that PQ ∥ EF or not.
Acc. to Thales Theorem,
PG/GE = GQ/FQ
Now,
3.9/3 ≠ 3.6/2.4
As we can see it is not prortional.
So, PQ is not parallel to EF.
Q.6) M and N are the points on the sides PQ and PR respectively, of a Δ PQR. For each of the following cases, state whether MN ∥ QR.
(i) PM = 4 cm, QM = 4.5 cm, PN = 4 cm, NR = 4.5 cm.
(ii) PQ = 1.28 cm, PR = 2.56 cm, PM = 0.16 cm, PN = 0.32 cm.
Sol: (i) It is given that PM = 4 cm, QM = 4.5 cm, PN = 4 cm, and NR = 4.5 cm.
We have to check that MN ∥ QR or not.
Acc. to Thales Theorem,
PM/QM = PN/NR
44.5 = 44.5
Hence, MN ∥ QR.
(ii) It is given that PQ = 1.28 cm, PR = 2.56 cm, PM = 0.16 cm, and PN = 0.32 cm.
We have to check that MN ∥ QR or not.
Acc. to Thales Theorem,
PM/QM = PN/NR
Now,
PM/MQ = 0.161.12 = 1/7
PN/NR = 0.322.24 = 1/7
Since,
0.161.12 = 0.322.24
Hence, MN ∥ QR.
Q.7) In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM ∥ AB and MN ∥ BC but neither of L, M, and N nor A, B, C are collinear. Show that LN ∥ AC.
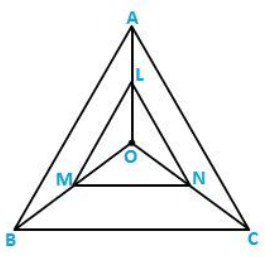
Sol: In Δ OAB, Since, LM ∥ AB,
Then, OL/LA = OM/MB (using BPT)
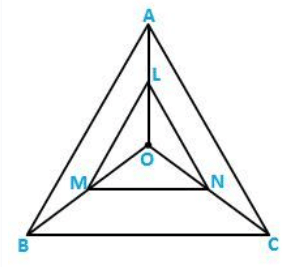
In Δ OBC, Since, MN ∥ BC,
Then, OM/MB = ON/NC (using BPT)
Therefore, ON/NC = OM/MB
From the above equations,
We get, OL/LA = ON/NC
In a Δ OCA,
OL/LA = ON/NC
LN ∥ AC (by converse BPT)
Q.8) If D and E are the points on sides AB and AC respectively of a Δ ABC such that DE ∥ BC and BD = CE. Prove that Δ ABC is isosceles.
Sol: It is given that in Δ ABC, DE ∥ BC and BD = CE.
We need to prove that Δ ABC is isosceles.
Acc. to Thales Theorem,
AD/BD = AE/EC
AD = AE
Now, BD = CE and AD = AE.
So, AD + BD = AE + CE.
Therefore, AB = AC.
Therefore, Δ ABC is isosceles.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-4.2 Triangles, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are the RD Sharma Solutions? |  |
| 2. What is the importance of studying triangles in Class 10 Mathematics? |  |
| 3. How can the RD Sharma Solutions for Class 10 Triangles help in exam preparation? |  |
| 4. Are the RD Sharma Solutions for Class 10 Triangles available online? |  |
| 5. Can the RD Sharma Solutions for Class 10 Triangles be used for self-study? |  |





















