Ex-8.5 Quadratic Equations, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download

Q.1: Find the discriminant of the following quadratic equations :

1:  2x²  – 5x + 3 = 0

Sol:  2x²  – 5x + 3 = 0

The given equation is in the form of ax²  + bx + c = 0

Here, a = 2 , b = -5 and c = 3

The discriminant, D = b²  – 4ac

D = (-5)²  –  4 x 2 x 3

D =   25 – 24 = 1

Therefore, the discriminant of the following quadratic equation is 1.

2)  x²  + 2x + 4 = 0

Sol:  x²  + 2x + 4 = 0

The given equation is in the form of ax²  + bx + c = 0

Here, a = 1 , b = 2 and c = 4

The discriminant is :-

D = (2)²  – 4 x 1 x 4

D = 4 – 16 = – 12

The discriminant of the following quadratic equation is = – 12.

3)   (x -1) (2x -1) = 0

Sol: (x -1) (2x -1) = 0

The provided  equation is (x -1) (2x -1) = 0

By solving it, we get  2x²  – 3x + 1 = 0

Now this equation is in the form of  ax²  + bx + c = 0

Here,  a =  2 , b = -3 , c = 1

The discriminant is :-

D = (-3)²  – 4 x 2 x 1

D =  9 – 8 = 1

The discriminant of the following quadratic equation is = 1.

4)  x²  – 2x + k = 0

Sol:  x²  – 2x + k = 0

The given equation is in the form of ax²  +   bx + c = 0

Here,  a = 1 , b = -2 , and c = k

D = b²  – 4ac

D = (-2)²   –  4(1)(k)

= 4 – 4k

Therefore, the discriminant, D  of the equation is (4 – 4k)

5)   √3x² + 2√2x – 2√3 = 0

Sol: √3x² + 2√2x – 2√3 = 0

The given equation is in the form of ax²  +   bx + c = 0

herea = √3,b = 2√2x and c = −2√3

The discriminant is,  D = b²  – 4ac

(2√2)² – (4×√3× – 2√3)

D  = 8 + 24 = 32

The discriminant, D of the following equation is 32.

6)  x²  – x + 1 = 0

Sol:    x²  – x + 1 = 0

The given equation  is in the form of ax²  + bx + c = 0

Here,  a = 1 , b = -1 and  c = 1

The discriminant is D = b²  – 4ac

(-1)²  – 4 x 1 x 1

1 – 4 = – 3

Therefore, The discriminant D of the following  equation is -3.

Q.2: 1)   16x²  =  24x + 1

Sol:  16x²  – 24x – 1 = 0

The given equation can be written in the form of,  ax²  +  bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a = 16 , b = -24 and c = – 1

Therefore, the discriminant is given as,

D = (-24)²  – 4(16)(-1)

= 576 + 64

= 640

For a quadratic equation to have real roots, D ≥  0.

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

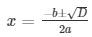
Therefore, the roots of the following equation are as follows,

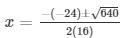
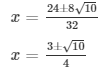
The values of x for both the cases will be :

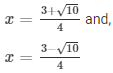
2)  x²  + x + 2 = 0

Sol:   x²  + x + 2 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a = 1, b = 1 and c = 2.

Therefore, the discriminant is given as,

D   = (1)²  –  4(1)(2)

=  1 – 8

= – 7

For a quadratic equation to have real roots, D ≥   0.

Here we find that the equation does not satisfy this condition, hence it does not have real roots.

 3) √3x² + 10x – 8√3 = 0

Sol:  √3x² + 10x – 8√3 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here,  a =  √3  , b = 10 and c =  −8√3

Therefore, the discriminant is given as,

D = (10)²  – 4(√3  )( −8√3) = 100 + 96 = 196

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

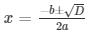
Therefore, the roots of the equation are given as follows,

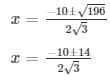
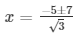
The values of x for both the cases will be :

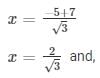
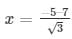
x = −4√3

4) 3x²  – 2x + 2 = 0

Sol:  3x²  – 2x + 2 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a = 3 , b = -2 and c = 2.

Therefore, the discriminant is given as,

D = (-2)²  – 4(3)(2)

= 4 – 24 = -20

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation does not satisfy this condition, hence it has no real roots.

5) 2x² – 2√6x + 3 = 0

Sol:  2x² – 2√6x + 3 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a = 2 , b =  −2√6  and   c = 3.

Therefore, the discriminant is given as,

D =  (−2√6)² – 4(2)(3)

= 24 – 24 = 0

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

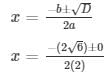
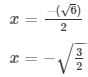
6)  3a²x²  + 8abx + 4b²  = 0

Sol:  3a²x²  + 8abx + 4b²  = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a = 3a², b = 8ab and c = 4b²

Therefore, the discriminant is given as,

D = (8ab)²  – 4(3a²)(4b²)

= 64a²b²  – 48a²b²  = 16a²b²

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

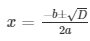
Therefore, the roots of the equation are given as follows,

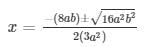
The values of x for both the cases will be :

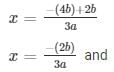
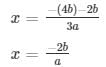
7.)  3x² + 2√5x – 5 = 0

Sol.:  3x² + 2√5x – 5 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a = 3,  b =  2√5   and c = – 5.

Therefore, the discriminant is given as,

D   =  (2√5)² – 4(3)(−5)

= 20 + 60

= 80

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

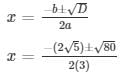
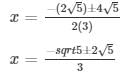
The values of x for both the cases will be :

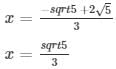
and ,

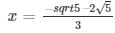
x = –  √5

8.)  x²  – 2x + 1 = 0

Sol.:  x²  – 2x + 1 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a = 1,  b = – 2 and c = 1

Therefore, the discriminant is given as,

D = (-2)²   – 4(1)(1)

=  4 – 4

= 0

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

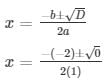
x = 2/2

x = 1

Therefore,  the  equation real roots   and its value is 1

9.)  2x² + 5√3x + 6 = 0

Sol.:  2x² + 5√3x + 6 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here,  a = 2, b =  5√3  and c = 6.

Therefore, the discriminant is given as,

D =  (5√3)²  –  4(2)(6)

= 75 – 48

= 27

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

Therefore, the roots of the equation are given as follows

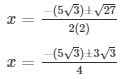
The values of x for both the cases will be :

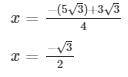
and ,

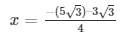
x = −2√3

10.)  √2x² + 7x + 5√2 = 0

Sol.:  √2x² + 7x + 5√2 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a =  √2 , b = 7 , c =  5√2

Therefore, the discriminant is given as,

D =  (7)² – 4(√2)(5√2)

D = 49 – 40

D = 9

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

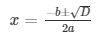
Therefore, the roots of the equation are given as follows,

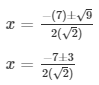
The values of x for both the cases will be :

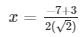
x = −√2

and

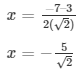
11.) 2x² – 2√2x + 1 = 0

Sol.:  2x² – 2√2x + 1 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a = 2 , b =   – 2√2 , c = 1

Therefore, the discriminant is given as,

D =  (−2√2)² – 4(2)(1)

= 8 – 8

= 0

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

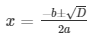
Therefore, the roots of the equation are given as follows,

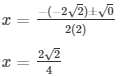
x = 1/√2
 

12.)  3x²  – 5x + 2 = 0

Sol.:  3x²  – 5x + 2 = 0

The given equation can be written in the form of,  ax²  +   bx + c = 0

the discriminant is given by the following equation,  D = b²  – 4ac

here, a = 3, b = -5 and c = 2.

Therefore, the discriminant is given as,

D = (-5)²  – 4(3)(2)

= 25 – 24

= 1

For a quadratic equation to have real roots,  D ≥ 0

Here it can be seen that the equation satisfies this condition, hence it has real roots.

the roots of an equation can be found out by using,

Therefore, the roots of the equation are given as follows,

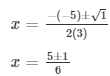
The values of x for both the cases will be :

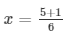
x = 1

and ,

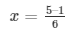
x = 2/3

Q.3)  Solve for x : 1.) 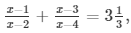x ≠ 2,4.

Sol.: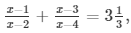 x ≠ 2,4

The above equation can be solved as follows:

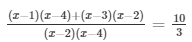
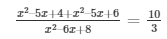
6x²  – 30x + 30 = 10x²  – 60x + 80

4x²  – 30x + 50 = 0

2x²  – 15x + 25 = 0

The above equation is in the form of ax²  + bx + c = 0

The discriminant is given by the equation, D = b²  – 4ac

Here, a = 2 , b = -15 , c = 25

D = (-15)²  – 4(2)(25)

= 225 – 200

= 25

the roots of an equation can be found out by using,

Therefore, the roots of the equation are given as follows,

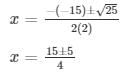
The values of x for both the cases will be :

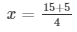
X  =   5

Also,

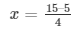
x = 5/2

2)   x + 1/x = 3,x≠0

Sol.:  x + 1/x = 3,x≠0

The above equation can be solved as follows:

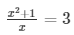
X²  + 1 = 3x

X²  – 3x + 1 = 0

The above equation is in the form of ax²  + bx + c = 0

The discriminant is given by the equation, D = b²  – 4ac

Here, a = 1 , b = – 3 , c = 1

D = (-3)²  – 4(1)(1)

D = 9 – 4

D = 5

the roots of an equation can be found out by using,

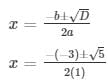
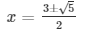
The values of x for both the cases will be :

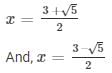
3.) 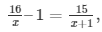 x≠0,−1

Sol. : 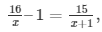  x≠0,−1

The above equation can be solved as follows:

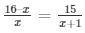
(16 – x)(x + 1) = 15x

16x + 16 – x²  – x = 15x

15x + 16 – x²  – 15x = 0

16 – x²  = 0

X²  – 16 = 0

The above equation is in the form of ax²  + bx + c = 0

The discriminant is given by the equation, D = b²  – 4ac

Here, a = 1 , b = 0 , c = -16

D = (0)²  – 4(1)(-16)

D = 64

the roots of an equation can be found out by using,

Therefore, the roots of the equation are given as follows,

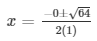
x = ± 8/2

x = ± 4