Ex-8.12 Quadratic Equations, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 1: A takes 10 days less than the time taken by B to finish a piece of work. If both A and B together can finish a work in 12 days, find the time taken by B to finish the piece of work.
Sol:
Let us consider B tales x days to complete the piece of work
B’s 1 day work = 1/x
Now, A takes 10 days less than that of B to finish the same piece of work that is (x - 10) days
A’s 1 day work = 
Same work in 12 days
(A and B)’s 1 day’s work = 1/12
According to the question
A’s 1 day work + B’s 1 day work = 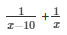
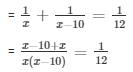
= 12(2x - 10) = x(x - 10)
= 24x - 120 = x2 - 10x
= x2 - 10x - 24x + 120 = 0
= x2 - 34x + 120 = 0
= x2 - 30x - 4x + 120 = 0
= x(x - 30) - 4(x - 30) = 0
= (x - 30)(x - 4) = 0
Either x - 30 = 0 therefore x = 30
Or, x - 4 = 0 therefore x = 4
We observe that the value of x cannot be less than 10 so the value of x = 30
Time taken by B to finish the piece of work is 30 days
Question 2: If two pipes function simultaneously, a reservoir will be filled in 12 hours. One pipe fills the reservoir 10 hours faster than the other. How many hours will the second pipe take to fill the reservoir?
Sol:
Let us assume that the faster pipe takes x hours to fill the reservoir
Portion of reservoir filled by faster pipe in one hour = 1/x
Now, slower pipe takes 10 hours more than that of faster pipe to fill the reservoir that is (x + 10 ) hours
Portion of reservoir filled by slower pipe = 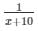
Given that, if both the pipes function simultaneously, the same reservoir can be filled in 12 hours
Portion of the reservoir filled by both pipes in one hour = 1/12
Now ,
Portion of reservoir filled by slower pipe in one hour + Portion of reservoir filled by faster pipe in one hour = 1/x + 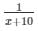
And portion of reservoir filled by both pipes = 1/12

= 12(2x + 10) = x(x + 10)
= x2 - 14x - 120 = 0
= x2 - 20x + 6x - 120 = 0
= x(x - 20) + 6(x - 20) = 0
= (x - 20)(x + 6) = 0
Either x - 20 = 0 therefore x = 20
Or, x + 6 = 0 therefore x = - 6
Since the value of time cannot be negative so the value of x is 20 hours
Time taken by the slower pipe to fill the reservoir = x + 10 = 30 hours
Question 3: Two water taps together can fill a tank in 938. The tap of larger diameter takes 10hours less than the smaller one to fill the tank separately. Find the time in which each tap can be fill separately the tank.
Sol:
Let the time taken by the tap of smaller diameter to fill the tank be x hours
Portion of tank filled by smaller pipe in one hour = 1/x
Now, larger pipe diameter takes 10 hours less than the smaller diameter pipe in one hour = 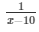
Given that,
Two taps together can fill the tank in 
= 75/8.
Now, portion of the tank filled by both the taps together in one hour
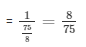
We have ,
Portion of tank filled by smaller pipe in one hour + Portion of tank filled by larger pipe in one hour
= 8/75
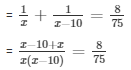
= 75(2x - 10) = 8x(x - 10)
= 150x - 750 = 8x2 - 80x
= 8x2 - 230x + 750 = 0
= 4x2 - 115x + 375 = 0
Here a = 4 , b = - 115 , c = 375
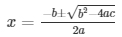
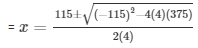
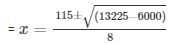
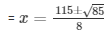
The value of x can either be 8 or 3.75 hours.
The value of x is 8 hours
Question 4: Two pipes running together can fill the tank in 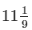 minutes. if one pipe takes 5 minutes more than the other to fill the tank separately. Find the time in which each pipe would fill the tank separately.
minutes. if one pipe takes 5 minutes more than the other to fill the tank separately. Find the time in which each pipe would fill the tank separately.
Sol:
Let us take the time taken by the faster pipe to fill the tank as x minutes
Portion of tank filled by faster pipe in one minute = 1/x
Now,
Time taken by the slower pipe to fill the same tank is 5 minutes more than that of faster pipe = x + 5 minutes
Portion of the tank filled by the slower pipe = 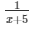
Given that,
The two pipes together can fill the tank in 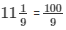
Portion of tank filled by two pipes together in 1 minute = 9/100
Portion of tank filled by faster pipe in one minute + Portion of the tank filled by the slower pipe
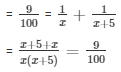
= 9x(x + 5) = 100(2x + 5)
= 9x2 + 45x = 200x + 500
= 9x2 - 155x - 500 = 0
= 9x2 - 180x + 25x - 500 = 0
= 9x(x - 20) + 25(x - 20) = 0
= (x - 20)(9x + 25) = 0
Either x - 20 therefore x = 20
Or, 9x + 25 = 0 therefore −259
Since time cannot be negative
So the value of x = 20 minutes
The required time taken to fill the tank is 20 minutes
Time taken by the slower pipe is x + 5 = 20 + 5 = 25 minutes
Times taken by the slower and faster pipe are 25 minutes and 20 minutes respectively.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-8.12 Quadratic Equations, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. How can I solve a quadratic equation using the quadratic formula? |  |
| 2. How do I find the roots of a quadratic equation if the discriminant is zero? |  |
| 3. Can a quadratic equation have no real roots? |  |
| 4. Is it possible for a quadratic equation to have two equal roots? |  |
| 5. How can I check if a given equation is quadratic or not? |  |





















