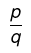Introduction to Number System | Mathematics (Maths) Class 9 PDF Download
Real Number System

Classification of Real Numbers
Numbers
In real life, we use Hindu Arabic numerals - a system which consists of the symbols 0 to 9.
This system of reading and writing numerals is called, “Base ten system” or “Decimal number system”.
Natural Numbers
Counting numbers are called natural numbers. These numbers start with the smallest number 1 and go on without end. The set of all natural numbers is denoted by the symbol ‘N’.
N = { 1, 2, 3, 4, 5, .......} is the set of all natural numbers.
Whole Numbers
Natural numbers together with zero (0) are called whole numbers. These numbers start with the smallest number 0 and go on without end.
The set of all whole numbers is denoted by the symbol ‘W’.
W = { 0, 1, 2, 3, 4, 5, .......} is the set of all whole numbers.
Integers
The whole numbers and negative numbers together are called integers.
The set of all integers is denoted by Z.
Z = {... - 2, - 1, 0, 1, 2, ...,} is the set of all integers
Fractions
A fraction is a part or parts of a whole.
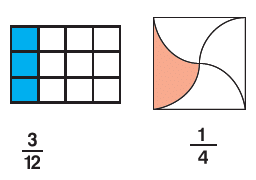 Fig: Fractions
Fig: FractionsIn a fraction, the number above the line is called the numerator and the number below the line is called the denominator.
Decimal Numbers
A number in which we have "point" is called a decimal number.
A decimal number has two parts namely an integral part and a decimal part.
Examples:
1) Let us consider the decimal number 0.6
0.6 can be written as 0 + 0.6
Here, integral part = 0 and decimal part = 6
2) Let us consider the decimal number 7.2
7.2 can be written as 7 + 0.2
Here, integral part = 7 and decimal part = 2
In a decimal number, the digits to the left of the decimal point is the integral part.
The digits to the right of the decimal point are the decimal part.
The value of all the decimal parts is less than 1.
Rational Numbers
Both "p" and "q" must be integers and q≠ 0
So, any number in the form of a fraction can be treated as a rational number.
Examples:
5, 2.3, 0.02, 5/6
Because all these numbers can be written as fractions.
5 = 5/1
2.3 = 23/10
0.02 = 2/100 = 1/50
5/6 (This is already a fraction)
Apart from the above examples, sometimes we will have recurring decimals like 1.262626..........
1.262626........ is a non-terminating recurring decimal.
All these recurring decimals can be converted into fractions and they are also rational numbers.
Important note:
All the fractions and decimal numbers will come under this category.
Hence, all the fractions and decimal numbers to be considered as rational numbers.
Irrational Numbers
A number that can not be converted into a fraction is called irrational numbers.
Examples:

All the above non-terminating numbers can not be converted into fractions because they do not have repeated patterns.
When we are trying to find the square root of a number that is not a perfect square, we get this non-repeating and non-terminating decimal.
And these non-recurring decimals can never be converted into fractions and they are called irrational numbers.
Decimal Expansions of Real Numbers
There are three types of decimal expansions of real numbers.
1. Terminating
2. Non-Terminating but Repeating
3. Non-Terminating and Non-Repeating
1. Terminating: The remainder becomes zero.
Let us take examples to know it.
Example 1:
Expansion of 7/4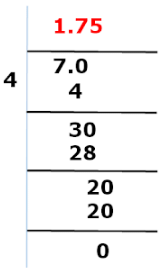 After performing some steps, we get the remainder as 0.
After performing some steps, we get the remainder as 0.
The remainder is 0, and the decimal expansion ends at 5. So it means the expansion is terminating.
Example 2:
Expansion of 32/5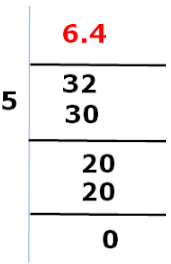 Again we found that after some steps the remainder becomes zero with the decimal expansion as 6.4.
Again we found that after some steps the remainder becomes zero with the decimal expansion as 6.4.
Similarly, the expansion of 32/5 is terminating.
Example 3:
Expansion of 578/25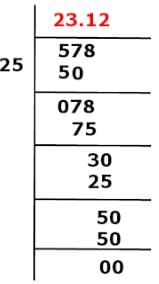 Decimal expansion of 578/25 = 23.12
Decimal expansion of 578/25 = 23.12
Therefore, the expansion of 578/52 is terminating.
2. The remainder never becomes zero: There are two cases:
(a) Non-Terminating but Repeating.
(b) Non-Terminating and Non-Repeating
Example: Expansion of 10/3 Decimal expansion of 10/3 = 3.333333...
Decimal expansion of 10/3 = 3.333333... 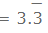
The expansion of 10/3 does not end that is not terminating, and number 3 is repeating, so it is a non-terminating but recurring expansion.
Example: Expansion of 1/7 Decimal expansion of 1/7 = 1.142857...
Decimal expansion of 1/7 = 1.142857...
The expansion of 1/7 does not end that is not terminating, and numbers 142857 are repeating, so it is a non terminating but recurring expansion.
1/7 = 
Example:
π is a non-terminating, non-repeating decimal. π = 3.141 592 653 589 793 238 462 643 383 279 ...
e is a non-terminating, non-repeating decimal. e = 2.718 281 828 459 045 235 360 287 471 352 ...
|
40 videos|471 docs|57 tests
|
FAQs on Introduction to Number System - Mathematics (Maths) Class 9
| 1. What is the real number system? |  |
| 2. What are decimal expansions of real numbers? |  |
| 3. How are real numbers related to the number system? |  |
| 4. What is the significance of understanding the real number system? |  |
| 5. Can all real numbers be expressed as a decimal expansion? |  |