Real Valued Functions | Mathematics (Maths) Class 12 - JEE PDF Download
FUNCTIONS
A function is a relation that maps each element x of a set A with one and only one element y of another set B. In other words, it is a relation between a set of inputs and a set of outputs in which each input is related with a unique output. A function is a rule that relates an input to exactly one output.
 It is a special type of relation. A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B and no two distinct elements of B have the same mapped first element. A and B are the non-empty sets. The whole set A is the domain and the whole set B is codomain.
It is a special type of relation. A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B and no two distinct elements of B have the same mapped first element. A and B are the non-empty sets. The whole set A is the domain and the whole set B is codomain.
Definition: A function is a rule (or a set of rules) which relates or associates each and every element of a non empty set A with the unique element of the non empty set B.
REPRESENTATION
A function f: A → B is represented as f(a) = b such that for a ∈ A there is a unique element b ∈ B such that (a, b) ∈ f.
For any function f, the notation f(a) is read as “f of a” and represents the value of b when a is replaced by the number or expression inside the parenthesis. The element b is the image of a under f and a is the pre-image of b under f.
The set ‘A’ is called the domain of ‘f’.
The set ‘B’ is called the co-domain of ‘f’.
Set of images (outputs) of different elements of the set A is called the range of ‘f’. It is obvious that range could be a subset of the co-domain as we may have some elements in the co-domain which are not the images of any element of A (of course, these elements of the co-domain will not be included in the range). Range is also called domain of variation.
If R is the set of real numbers and A and B are subsets of R, then the function f (A) is called a real−valued function or a real function.
Domain of a function ‘f’ is normally represented as Domain (f). Range is represented as Range (f). Note that some times domain of the function is not explicitly defined. In these cases domain would mean the set of values of ‘x’ for which f (x) assumes real values that is if y = f (x) then called Domain (f) = {x : f (x) is a real number}.
In other words, domain is defined as a set of all those values of x for which the given function is defined.
Note: Every function is a relation but every relation need not be a function.
For example: Let A = {1, 2, 3}
R1 = {(1, 1), (2, 3), (3, 3)}
R2 = {(1, 1)(1, 2), (3, 2)(2, 1)}
Here R1 is a function but R2 is not a function because here element 1 has two images as 1 and 2.
Q. Which of the following is a function?


 Ans. Figure 3 is an example of function since every element of A is mapped to a unique element of B and no two distinct elements of B have the same pre-image in A.
Ans. Figure 3 is an example of function since every element of A is mapped to a unique element of B and no two distinct elements of B have the same pre-image in A.
Q. Find the domain and range of the function 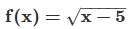
Ans. The function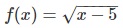
is defined for x ≥ 5
⇒ The domain is [5, ∞] .
Also, for any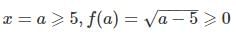
⇒ The range of the function is [0, ∞] .
Q. Find the domain and the range of the function y = f (x), where f (x) is given by
(i) x2 − 2x − 3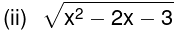
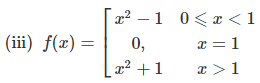
(iv) tan x
(v) tan−1x
(vi) log10 (x).
(vii) sin x
Ans.
(i) Here y = (x − 3) (x + 1).
The function is defined for all real values of x
⇒ Its domain is R.
Also x2 − 2x − 3 − y = 0 for real x
⇒ 4 + 4 (3 + y) ≥ 0 ⇒ − 4 ≤ y < ∞.
Hence the range of the given function is [- 4, ∞].
(ii) Here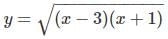
⇒ (x − 3) (x + 1) ≥ 0 so that x ≥ 3 or x ≤ − 1.
Hence the domain is R − (− 1, 3) or (− ∞, - 1] ∪ [3, ∞].
Since f(x) is non−negative in the domain, the range of f (x) is the interval [0, ∞].
(iii) The given function is defined for all x ≥ 0
⇒ The domain is [0, ∞].
Moreover - 1 ≤ f (x) < ∞
⇒ The range is [- 1, ∞].
(iv) The function f (x) = tan x = sin x/cos x is not defined when
cos x = 0, or x = (2n + 1) π/2, n = 0, ± 1, ± 2, …….
Hence domain of tan x is R -{(2n + 1)π/2, n = 0, + 1, + 2,....}, and its range is R.
(v) The function f (x) = tan−1 x, is defined for all real values of x and -π/2 < tan-1 < π/2.
Hence its domain is R and the range is (-π/2, π/2).
(vi) The function f (x) = log10 x is defined for all x > 0. Hence its domain is (0, ∞) and range is R.
(vii) The function f (x) = sin x, (x in radians) is defined for all real values of x
⇒ domain of f (x) is R. Also − 1 ≤ sin x ≤ 1, for all x,
so that the range of f (x) is [− 1, 1].
Different types of functions and their graphical representation
Identity function
A function f:R → R is said to be an identity function if f(x) = x, ∀ x ϵ R denoted by IR.
Let A = {1, 2, 3}
The function f: A → A defined by f(x) = x is an identity function.
f = {(1,1), (2,2), (3,3)}.
The graph of an identity function is a straight line passing through the origin.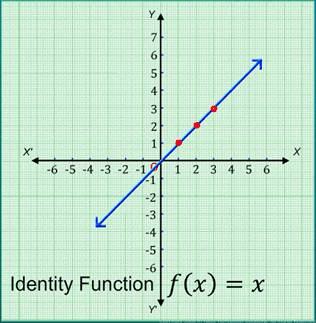
Each point on this line is equidistant from the coordinate axes.
The straight line makes an angle of 45° with the coordinate axes.
Example:
Let A = {1, 2, 3, 4, 5, 6}
Then Identity function on set A will be defined as
IA : A → A , IA = x , x ∈ A
for x = 1 , IA(1) = x = 1
for x = 2 , IA(1) = x = 2
for x = 3 , IA(1) = x = 3
for x = 4 , IA(1) = x = 4
for x = 5 , IA(1) = x = 5
Domain, Range and co-domain will be Set A
Constant function
A function f:R → R is said to be a constant function, if f(x) = c , ∀ x ϵ R, where c is a constant.
Let f:R → R be a constant function defined by f(x) = 4 , ∀ x ϵ R.
The ordered pairs satisfying the linear function are: (0, 4), (-1, 4), (2, 4).
If the range of a function is a singleton set, then it is known as a constant function.
On plotting these points on the Cartesian plane and then joining them, we get the graph of the constant function f of x = 4,∀ x ϵ R as shown.

Also, from the graph, we can conclude that the graph of a constant function, f(x) = c, is always a straight line parallel to the X-axis, intersecting the Y-axis at (0, c).
Q. Which of the graph represent a constant function?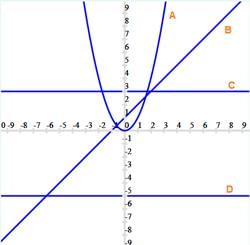 Ans.
Ans.
The graph should be parallel to x-axis for the function to be constant function
So C and D are constant function.
Polynomial function
A polynomial function is defined by y = a0 + a1x + a2x2 + … + anxn, where n is a non-negative integer and a0, a1, a2,…, n ∈ R. The highest power in the expression is the degree of the polynomial function. Polynomial functions are further classified based on their degrees:
If the degree is zero, the polynomial function is a constant function (explained above).
Examples of polynomial functions
f(x) = x2 + 5x + 6 ,∀ x ϵ R (Degree is 2)
and f (x) = x3 + 4x + 2 ,∀ x ϵ R (Degree is 3)
Note: In a polynomial function, the powers of the variables should be non-negative integers.For example, f(x) = √x + 2 (∀ x ϵ R) is not a polynomial function because the power of x is a rational number.
Consider the polynomial function, f(x) = 3x2 +2x -3 ,∀ x ϵ RThe ordered pairs satisfying the polynomial function are (0, -3), (-1, -2), (1, 2), (2, 13), (-2, 5).
On plotting these points on the Cartesian plane and then joining them, we get the graph of the polynomial function f of x is equal to 3 x2 + 2 x - 3 ,∀ x ϵ R as shown.
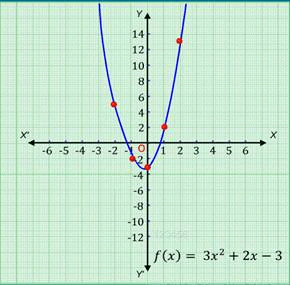
Linear function
A function f:R → R is said to be a linear function if f (x) = ax + b, where a ≠ 0, a and b are real constants, and x is a real variable. It is a polynomial function with degree one.
Consider the linear function, f(x) = 3x + 7, ∀ x ϵ R
The ordered pairs satisfying the linear function are (0, 7), (-1, 4), (-2, 1).
On plotting these points on the Cartesian plane and then joining them, we get the graph of the linear function f of x is equal to 3x + 7, ∀ x ϵ R as shown in the figure.
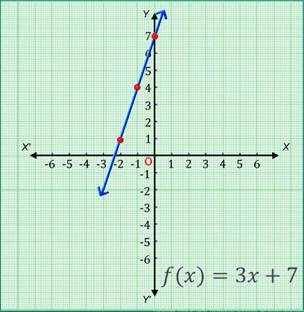
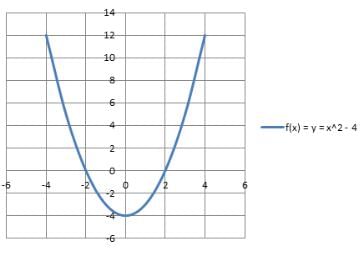
Quadratic Function: If the degree of the polynomial function is two, then it is a quadratic function. It is expressed as f(x) = ax2 + bx + c, where a ≠ 0 and a, b, c are constant & x is a variable. The domain and the range are R. The graphical representation of a quadratic function say, f(x) = x2 – 4 is
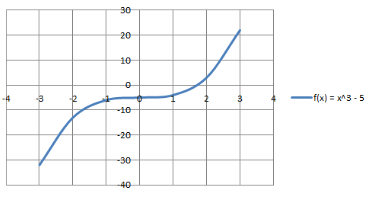
Cubic Function: A cubic polynomial function is a polynomial of degree three and can be denoted by f(x) = ax3 + bx2 + cx +d, where a ≠ 0 and a, b, c, and d are constant & x is a variable. Graph for f(x) = y = x3 – 5. The domain and the range are R.
Rational function
If f(x) and g(x) be two polynomial functions, then f(x)/g(x) such that g(x) ≠ 0 and ∀ x ϵ R, is known as a rational function.
Let us consider the function f ( x) = 2x -5/3x - 2 (x ≠ ⅔).
The ordered pairs satisfying the polynomial function are: (0, 5), (2, -¼), (1, -3).
On plotting these points on the Cartesian plane and then joining them, we get the graph of the given rational function as shown.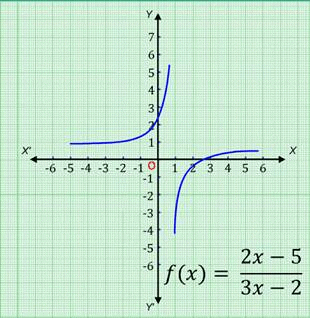
Modulus function
A function f: R → R defined by f(x) = |x| (∀ x ϵ R) is known as a modulus function.
If x is negative, then the value of the function is minus x, and if x is non-negative, then the value of the function is x. i.e. f(x) = x if x ≥ 0 = - x if x < 0.
The ordered pairs satisfying the polynomial function are (0, 0), (-1, 1), (1, 1), (-3, 3), (3, 3).
On plotting these points on the Cartesian plane and then joining them, we get the graph of modulus function f of x is equal to mod of x.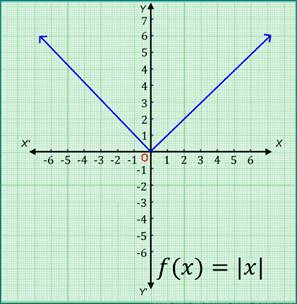
Greatest integer function
A function f: R → R defined by f(x) = [x],∀ x ϵ R assumes the value of the greatest integer, less than or equal to x.
From the definition of [x], we can see that
[x] = -1 for -1 £ x < 0
[x] = 0 for 0 £ x < 1
[x] = 1 for 1 £ x < 2
[x] = 2 for 2 £ x < 3, and so on.
⇒ f(2.5) will give the value 2 and f(1.2) will give the value 1, and so on…
Hence, the graph of the greatest integer function is as shown.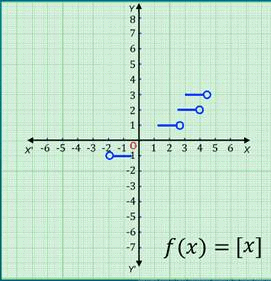
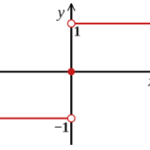
Signum Function
A function f: R→ R defined by
f(x) = { 1, if x > 0; 0, if x = 0; -1, if x < 0
Signum or the sign function extracts the sign of the real number and is also known as step function.
Trigonometric function
(i) Function: f(x) = sin x
Domain: x ∈ R
Range: y ∈ [–1, 1]
Curve:
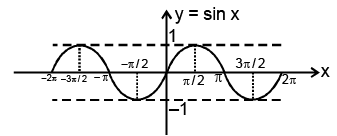
(ii) Function: f(x) = cos x
Domain: x ∈ R
Range: y ∈ [–1, 1]
Curve: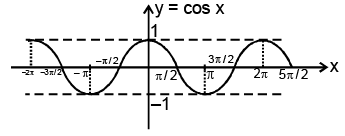
(iii) Function: f(x) = tan x
Domain: x ∈ R
Range: y ∈ R
Curve: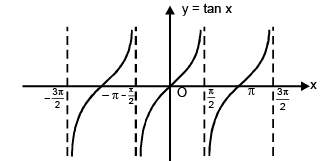
(iv) Function: f(x) = cot x
Domain: x ∈ R – (2n + 1) π / 2, n ∈ I
Range: y ∈ R
Curve: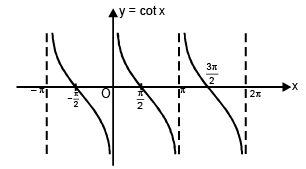
(v) Function: f(x) = cosec x
Domain: x ∈ R – nπ, n ∈ I
Range: y ∈ (-∞, –1] ∪ [1, ∞)
Curve: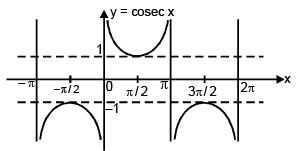
(vi) Function: f(x) = sec x
Domain: x ∈ R – (2n + 1) π / 2 , n ∈ I
Range: y ∈ (-∞, –1] ∪ [1, ∞)
Curve: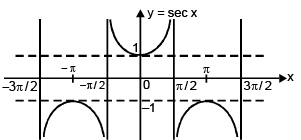
Algebraic Function
A function is called an algebraic function. If it can be constructed using algebraic operations such as additions, subtractions, multiplication, division taking roots etc.
All polynomial functions are algebraic but converse is not true
Example: f(x) =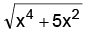 + x + (x3 + 5)3 / 5, f(x) = x3 + 3x2 + x + 5
+ x + (x3 + 5)3 / 5, f(x) = x3 + 3x2 + x + 5
Remark : Function which are not algebraic are called as transcendental function.
Example: 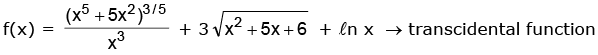
Example: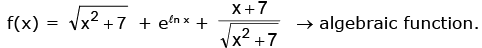
Logarithmic function
f(x) = logax, where x > 0, a > 0, a ≠ 1
a → base, x → number or argument of log.
Case – I : 0 < a < 1
f(x) = loga x
Domain : x ∈ (0, ∞)
Range : y ∈ R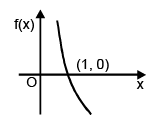
Case – II : a > l
f(x) = ln x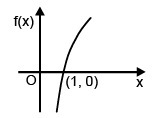
Exponential function
f(x) = ax, where a > 0, a ≠ 1
a → Base x → Exponent
Case – I : 0 < a < 1 ; a = 1 / 2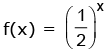
Domain : x ∈ R
Range : y ∈ (0, ∞)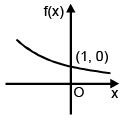
Case – II : a > 1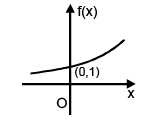
Fractional part function
y = f(x) = {x} = x – [x]
Domain : x ∈ R; Range : [0, 1)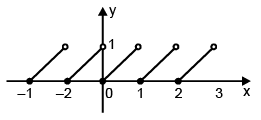
Example: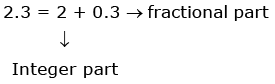
Properties:
(i) Fractional part of any integer is zero.
(ii) {x + n} = {x}, n ∈ I
(iii)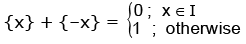
Examples
Example.1. Find the range of the following functions:
(a)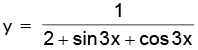
(b)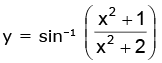
Ans. (a) We have,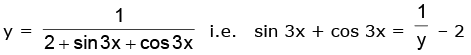
i.e. 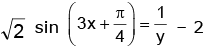
i.e.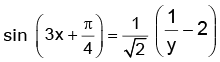
since, 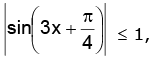
therefore we have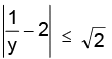
i.e.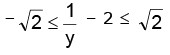
i.e.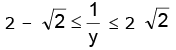
i.e.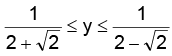
Hence, the range is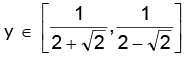
(b) We have,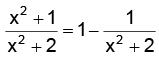
Now, we have 2 ≤ x2 + 2 < ∞ i.e.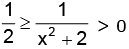
i.e.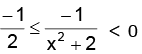
i.e.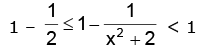
i.e.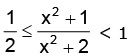
i.e.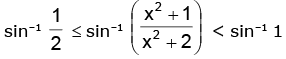
gives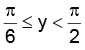
Hence, the range is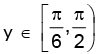
Example.2. Find the range of following functions :
(i) y = ln (2x – x2)
(ii) y = sec – 1 (x2 + 3x + 1)
Solution. (i) using maxima–minima, we have (2x – x2) ∈ (–∞, 1]
For log to be defined accepted values are 2x – x2 ∈ (0, 1] {i.e. domain (0, 1]}
ln (2x – x2) ∈ (0, 1] ∴ range is (–∞, 0]
(ii) y = sec–1 (x2 + 3x + 1)
Let t = x2 + 3x + 1 for x ∈ R then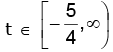
but y = sec–1 (t)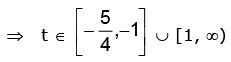
from graph range is
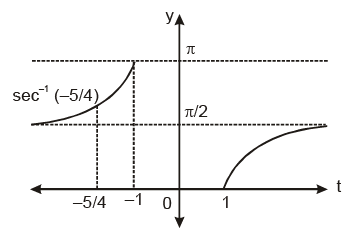
Example.3. Find the range of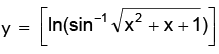
Solution. We have,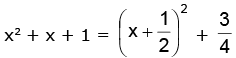 which is a positive quantity whose minimum value is 3 / 4.
which is a positive quantity whose minimum value is 3 / 4.
Also, for the function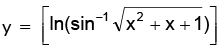 to be defined, we have x2 + x + 1 ≤ 1
to be defined, we have x2 + x + 1 ≤ 1
Thus, we have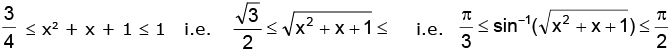
[∴ sin-1 x is an increasing function, the inequality sign remains same]
i.e.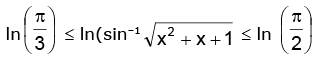
i.e.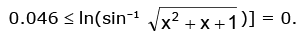
Hence, the range is y ∈ [ln π / 3, ln π / 2]
Example.4.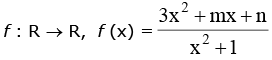 .If the range of this function is [– 4, 3) then find the value of (m2 + n2).
.If the range of this function is [– 4, 3) then find the value of (m2 + n2).
Solution.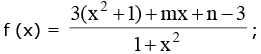
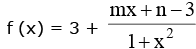
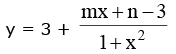 for y to lie in [– 4, 3) mx + n – 3 < 0 ∀ x ∈ R
for y to lie in [– 4, 3) mx + n – 3 < 0 ∀ x ∈ R
this is possible only if m = 0 when, m = 0 then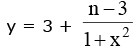
note that n - 3 < 0 (think !) n < 3 if x → ∞, ymax → 3-
now ymin occurs at x = 0 (as 1 + x2 is minimum)
ymin = 3 + n - 3 = n ⇒ n = - 4 so m2 + n2 = 16
Example.5. Find the domain and range of f(x) =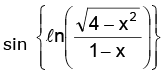
Solution.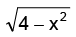 is positive and x2 < 4 ⇒ –2 < x < 2
is positive and x2 < 4 ⇒ –2 < x < 2
1 – x should also be positive. ∴ x < 1
Thus the domain of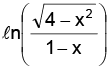 is –2 < x < 1 sine being defined for all values, the domain of sin
is –2 < x < 1 sine being defined for all values, the domain of sin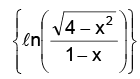 is the same as the domain of
is the same as the domain of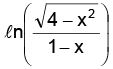
To study the range. Consider the function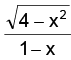
As x varies from –2 to 1,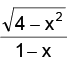 varies in the open interval (0, ∞) and hence
varies in the open interval (0, ∞) and hence
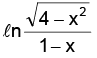 varies from –∞ to + ∞. Therefore the range of sin
varies from –∞ to + ∞. Therefore the range of sin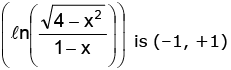
Example.6. Find the range of the function f(x) =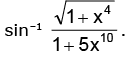
Solution. Consider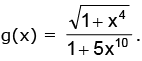 Also g(x) is positive ∀ x ∈ R and g(x) is continuous ∀ x ∈ R and g(0) = 1 and
Also g(x) is positive ∀ x ∈ R and g(x) is continuous ∀ x ∈ R and g(0) = 1 and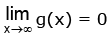
⇒ g(x) can take all values from (0, 1] ⇒ Range of f(x) = sin–1 (g(x)) is (0, π / 2]
Example.7.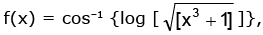 find the domain and range of f(x) (where [ * ] denotes the greatest integer function).
find the domain and range of f(x) (where [ * ] denotes the greatest integer function).
Solution. If cos–1 x = θ, then– 1 ≤ x ≤ 1
∴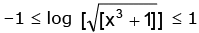
⇒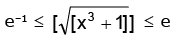
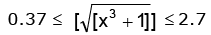
∴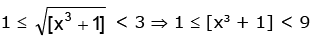
1 ≤ [x3] + 1 < 9 0 ≤ [x3] < 8 ∴ 0 ≤ x < 2
∴ Domain of f(x) = Dr in x ∈ [0, 2) Range of f(x) When 0 ≤ x < 2
Then 1 ≤ x3 + 1 < 9 ∴ 1 ≤ [x3 + 1] ≤ 8
⇒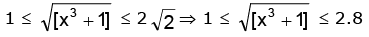
Case I: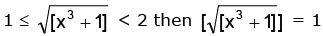
∴ Range in cos–1 {log 1} and cos–1 {log 2}
Case II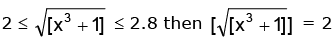
∴ Rf is (π / 2, cos–1 (log 2))
Example.8. Find the range of the following functions
(i) f(x) = loge (sinx sinx + 1) where 0 < x < π / 2.
(ii) f(x) = loge (2 sin x + tan x - 3x + 1) where π / 6 ≤ x ≤ π /3
Solution. (i) 0 < x < π / 2 ⇒ 0 < sin x < 1
Range of loge (sin xsin x + 1) for 0 < x < π / 2 = Range of loge (xx + 1) for 0 < x < 1
Let h(x) = xx + 1 = exlogex + 1
h'(x) = exlogex (1 + loge x) ⇒ h'(x) > 0 for x > 1/e and h'(x) < 0 for x < 1/e
∴ h(x) has a minima at x = 1/e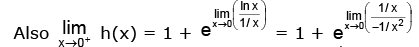
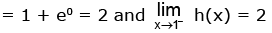
∴ 0 < x< 1
⇒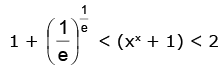
⇒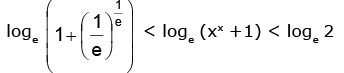
∴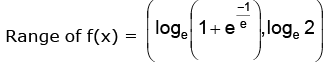
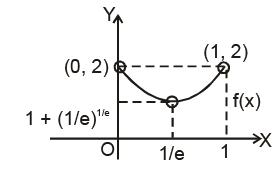
(ii) Let h(x) = (2 sin x + tan x – 3x +1) ⇒ h'(x) = (2 cos x + sec2 x – 3)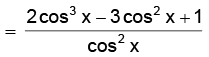
∴ h'(x) > 0 ⇒ 2 cos3 x – 3 cos2 x + 1 > 0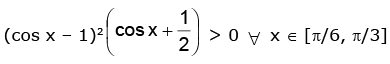
⇒ h(x) is an increasing function of x
⇒ h(π / 6) ≤ h(x) ≤ h(π / 3)
⇒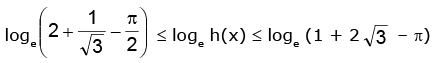
∴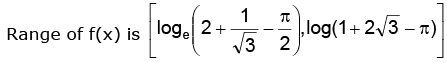
|
204 videos|290 docs|139 tests
|
FAQs on Real Valued Functions - Mathematics (Maths) Class 12 - JEE
| 1. What is a real-valued function? |  |
| 2. What is the difference between a real-valued function and a complex-valued function? |  |
| 3. What are the common types of real-valued functions? |  |
| 4. What is the domain and range of a real-valued function? |  |
| 5. How are real-valued functions used in real-life applications? |  |

|
Explore Courses for JEE exam
|

|

















