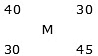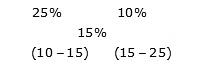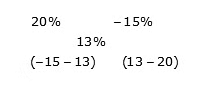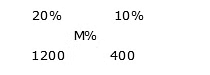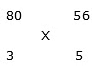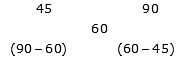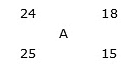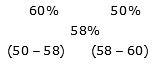Important Concepts: Alligation & Mixture | CSAT Preparation - UPSC PDF Download
| Table of contents |

|
| What are Mixtures & Alligations? |

|
| Types of Mixtures |

|
| Rules of Alligation |

|
| Important Formulae |

|
| Applications of Alligations |

|
Mixtures and Alligations is an essential topic that focuses on problems involving the blending of two or more ingredients with varying characteristics, such as price, concentration, or quantity.

What are Mixtures & Alligations?
- Mixing things together is called a mixture.
- Alligation helps us figure out how much of each thing is mixed together and at what price they are sold to make a profit or suffer a loss.
- To solve mixture and alligation problems, you need to understand that alligation helps find the average value of a mixture when the ratio and quantity of the ingredients mixed are different.
- It also helps figure out the proportion in which the elements are mixed.

Types of Mixtures
- Simple Mixtures:- When two or more different ingredients are mixed together, a simple mixture is formed. The sums based on simple mixtures are pretty straightforward and easy to solve.
For example,
Alloys are mixtures of two or more metals. Alloys are simple mixtures. - Compound Mixtures:- When two or more simple mixtures are mixed together, a compound mixture is formed. Hence, more ratios need to be calculated while solving the sum of complex mixtures.
For example,
When two metal alloys made from a combination of different elements are mixed together, then it leads to the formation of a complex mixture.
Rules of Alligation
- The rule enables us to find the ratio in which two or more ingredients/mixtures of different prices/concentrations are mixed together to form a final mixture or desired price or concentration.
- Two methods are used are mentioned below
Method 1: (Formula Method)
- It is given as-

- This rule can also be applied when a cheaper substance is mixed with an expensive substance.
- Example:Two types of wheat are sold at ₹45 per kg and ₹60 per kg. If a shopkeeper wants to make a mixture worth ₹54 per kg, what should be the ratio of the two types of wheat?
Ans: 2:3
Sol:
Using the Formula, we get
60 − 54 54 − 45 = 69 = 23
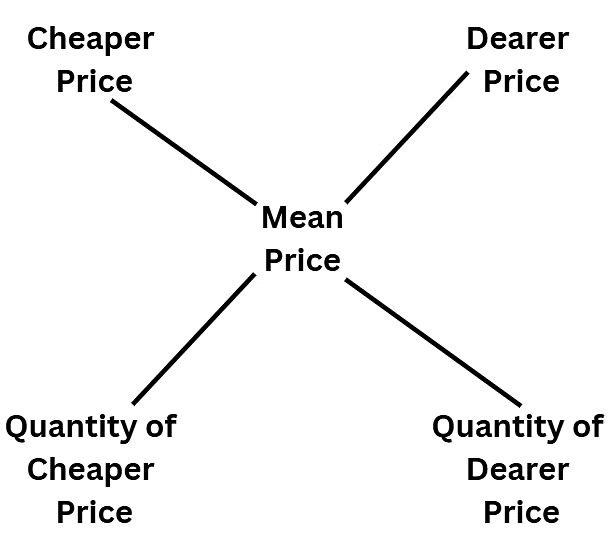
Method 2: (Diagram Method)
- The above method can be expressed using a diagram which will be more convenient to understand-
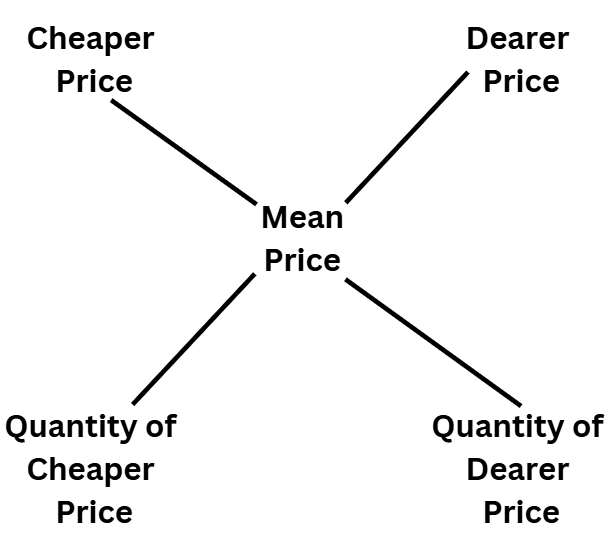
- The working of this formula is
Step 1: We take the positive difference of mean price and cheaper price and write the difference in the place of the Quantity of dearer price.
Step 2: Similarly, take the positive difference of the mean price and the dearer price and write the difference in the place of the Quantity of the cheaper price. - Example: How many litres of pure water should be added to 40 litres of 30% milk solution so that the resultant mixture is a 15% milk solution?
Sol: Taking milk as the common element in both solutions, we have 30% milk in the first and 0% milk in the second solution (i.e. pure water). On mixing them, we got 15% milk in the final solution. Therefore,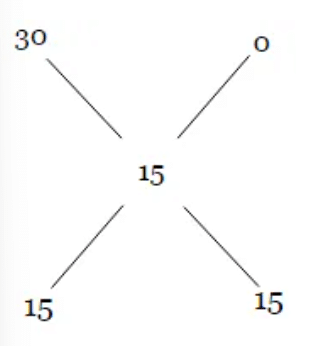 Or the ratio of the quantity of first and second solution should be 15:15 = 1:1
Or the ratio of the quantity of first and second solution should be 15:15 = 1:1Hence, 40 litres of pure water should be mixed to get the desired new solution.
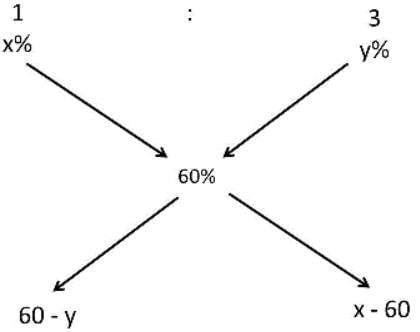
What Exactly is an Alligation?
- It is the reverse of weighted average; i.e. if the averages of two groups are separately given and the average of the whole group is given, then we can find out the ratio between the groups.
- For example, If the average weight of the boys in the class is 60 and the average weight of the girls in the class is 40 and average weight of the whole class is 52. Find the ratio between boys and the girls.
Sol: Average weight of boys = 60,
Average weight of girls = 40 and
Average weight of the whole class = 52
The data can be represented in an Alligation chart as given below and use it to find the ratio between the number of boys and girls in the class.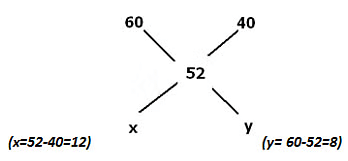 Take the difference across: x = 60-52 = 8 and y = 52-40 = 12.
Take the difference across: x = 60-52 = 8 and y = 52-40 = 12.
That is how we get the ratio between the boys and girls as 12:8 or 3:2.
Important Formulae
As we have studied in this chapter, we just have two important formulas to solve all the questions
1. 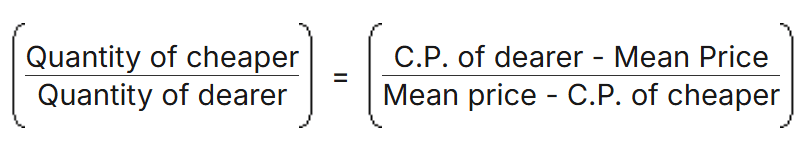
It is also called the rule of alligation and can also be represented as
2. 
Applications of Alligations
Alligation in Mixture Problems
We will see how the rule of alligation can be applied in mixture problems-
Example 1: A shopkeeper mixes 30 kg of type A rice at Rs.40/kg and 45 kg of type B rice at Rs.30/kg, then finds the price of a formed mixture of rice.
Sol:
By the rule of alligation:
(30 – M): (M – 40) = 30: 45 = 2: 3
90 – 3M = 2M – 805M = 170M = 34
Hence, price of mixture = Rs.34/kg
Note: After applying the concept of alligation on the price of the item of concentration of mixture we will get the ratio in which these two items or mixture are mixed.
Sol: Water percent in mixture A = 100% – 75% of 25%
By the rule of alligation:Required ratio = -5: -10
= 1: 2
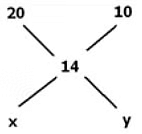
Example 3: In what ratio should a shopkeeper mix two types of rice, one costing 20 rupees/kg and another costing 10 rupees/kg to get a rice variety costing 14 rupees/kg?
Sol: Here also we can use Alligation as follows:
x = 14-10 = 4
y = 20-14 = 6
The ratio between the type 1 and type 2 rice is 4:6 or 2:3
Alligation in Profit and Loss Problems
Example 1: A shopkeeper sells type A rice at 20% profit and type B rice at 15% loss. If overall he earns 13% profit, then find the cost price of type A rice to type B rice.
Sol: By the rule of alligation:
The ratio of the cost price of type A to type B rice = -28: -7
= 4: 1
Note: After applying alligatiion concept in profit/loss percent earned on the items we will get the ratio of cost prices of the items.

Example 2: A shopkeeper purchased a table for Rs.1200 and sold it at 20% profit, he purchased a chair at Rs.400 and sold it at 10% profit, the find the overall profit percent earned by him.
Sol: Let overall profit percent = M%
By the rule of alligation:
(10 – M): (M – 20) = 1200: 400 = 3: 1
10 – M = 3M – 60
4M = 70
M = 17.5
Hence, overall profit percent = M = 17.5%
Alligation in Speed, distance, and Time Problems
The concept of mixture and alligation can be used to find the average speed of journey.
Example 1: A person covers the first 3 hours of a journey with a speed 80 km/h and the remaining 5 hours with a speed 56 km/h, then find his average speed of the journey.
Sol: Let average speed = X
By the rule of alligation:
(56 – X): (X – 80) = 3: 5
280 – 5X = 3X – 240
8X = 520
X = 65
Average speed of journey = 65 km/h
Note: After applying the concept of alligation on speed on different parts of the journey we will get the ratio of time taken to cover those parts.
Example 2: A distance of 360 km can be covered in 6 hours when some part of the journey is covered with speed 45 km/h and remaining with speed 90 km/h, then find the distance covered with speed 45 km/h.
Sol: Average speed of the journey = 360/6 = 60 km/h
By the rule of alligation:
Ratio of time taken = 30: 15 = 2: 1
Time for which journey is covered with speed 45 km/h = 6 * (2/3) = 4 hours
Distance covered by 45 km/h speed = 45 * 4 = 180 km
Alligation in Simple/Compound Interest Problems
The concept of alligation can be applied to SI and CI if we can calculate the effective interest rate for given time period.
For example:
Equivalent of 20% SI for 3 years = 20% * 3 = 60%
Equivalent of 20% CI for 2 years = [(1.2)2 – 1] * 100 = 44%
Example: Rahul lent Rs.5000 to Sumit at 25% SI for 2 years and borrowed Rs.3000 from Suresh for 3 years 10% SI, then find the profit/loss on interest amount of Rahul.
Sol: Effective rate of interest for 2 years on lent amount = 25% * 2 = 50%
Effective rate of interest for 3 years on borrowed amount = -10% * 3 = -30% [Negative because interest will be given.]
By the rule of alligation:
(-30 – X): (X – 50) = 5000: 3000 = 5: 3
-90 – 3X = 5X – 250
8X = 160
X = 20
Hence, total profit on interest amount = 20% of (5000 + 3000) =
= Rs.1600
Note: After applying the alligation concept in effective interest rate we will get the ratio of amount invested.
Alligation in Average, Ratio, and Percentage Problems
By applying the rule of alligation we can solve the problems of averages, ratios, and percentages quickly.
Example 1: Average age of a 25 students of a class is 24 years and average age of remaining 15 students of the class is 18 years, then find the average age of the class.
Sol: Let average age of class = A
By the rule of alligation:
(18 – A): (A – 24) = 25: 15 = 5: 3
54 – 3A = 5A – 120
8A = 174
A = 21.75
Hence, average age of the class = A = 21.75 years
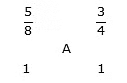
Example 2: Ratio of marks obtained to maximum marks by Arun in math and English is 5: 3 and 3: 1. If maximum marks in both the subjects are same, then find the ratio of marks obtained to maximum marks by Arun when both the subjects are taken together.
Sol: By the rule of alligation:
(3/4 – A): (A – 5/8) = 1: 1
3/4 – A = A – 5/8
2A = 11/8
A = 11/16
Required ratio = 11: (16 – 11) = 11: 5
Example 3: In states A and B out of the total population, the male population is 60% and 50% respectively. If the male population, when both the states are taken together, becomes 58% of the total population, then find that total population of state B is what percent of that of state A.
Sol: By the rule of alligation:
Ratio of total population of state A to that of state B = -8: -2 = 4: 1
Required percent = (1/4) * 100
= 25%
|
208 videos|272 docs|138 tests
|
FAQs on Important Concepts: Alligation & Mixture - CSAT Preparation - UPSC
| 1. What is the definition of mixtures in the context of alligation? |  |
| 2. What are the different types of mixtures commonly studied in alligation? |  |
| 3. What are the basic rules of alligation in problem-solving? |  |
| 4. What are some important formulae related to alligation? |  |
| 5. What are some practical applications of alligation in real life? |  |