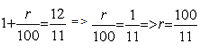Interests: Solved Examples | CSAT Preparation - UPSC PDF Download

Solved Examples
Que 1: A person invested a total amount of Rs. 15 lakh. A part of it was invested in a fixed deposit earning 6% annual interest, and the remaining amount was invested in two other deposits in the ratio of 2:1, earning annual interest at the rates of 4% and 3%, respectively. If the total annual interest income is Rs. 76,000, then the amount (in Rs. lakh) invested in the fixed deposit was
(a) 9 lakh
(b) 10 lakh
(c) 9.5 lakh
(d) 1.8 lakh
Ans: Option 1
Sol:
Let's say the amount invested in two other schemes are 200x and 100x at 4% and 3% respectively.
So, Amount invested in a fixed deposit = 1500000 – 300x
Two other schemes are 200x and 100x at 4% and 3%, respectively.
Total annual interest = 6% of (1500000 – 300x) + 4% of 200x + 3% of 100x = 76000
⇒ 90000 – 18x + 8x + 3x = 76000
⇒ x = 2000
Therefore, the amount deposited in a fixed deposit = 1500000 – 600000 = 900000 = 9 lakh
Hence, the correct answer is option (1).
Que 2: What will Rs.1500 amount to in three years if it is invested in 20% p.a. compound interest, interest being compounded annually?
(a)2400
(b) 2592
(c) 2678
(d) 2540
Ans: Option 2
Sol:
The usual way to find the compound interest is given by the formula A = P(1+r/100)n
In this formula,
A is the amount at the end of the period of investment
P is the principal that is invested
r is the rate of interest in % p.a
And n is the number of years for which the principal has been invested.
In this case, it would turn out to be A =1500(1+20/100)3
= 2592.
Que 3: If a sum of money grows to 144/121 times when invested for two years in a scheme where interest is compounded annually, how long will the same sum of money take to treble if invested at the same rate of interest in a scheme where interest is computed using simple interest method?
(a) 9 years
(b) 22 years
(c) 18 year
(d) 33 years
Ans: Option 2
Sol: The sum of money grows to times in 2 years.
If P is the principal invested, then it has grown to P in two years when invested in compound interest.
In compound interest, if a sum is invested for two years, the amount is found using the following formula= 144/121 P in this case.
=>=>
If r = 100/11 % then in simple interest the time it will take for a sum of money to treble is found out as follows:
Let P be the principal invested. Therefore, if the principal trebles = 3P, the remaining 2P has come on account of simple interest.
Simple Interest = Pnr/100 , where P is the simple interest, r is the rate of interest and ‘n’ is the number of years the principal was invested.
Therefore, 2P ==> 2 = n/11 or n = 22 years.
Que 4: The population of a town was 3600 three years back. It is 4800 right now. What will be the population three years down the line, if the rate of growth of population has been constant over the years and has been compounding annually?
(a) 6000
(b) 6400
(c) 7200
(d) 9600
Ans: Option 2
Sol: The population grew from 3600 to 4800 in 3 years. That is a growth of 1200 on 3600 during three-year span.
Therefore, the rate of growth for three years has been 1200/3600 = 1/3
The rate of growth during the next three years will also be the same.
Therefore, the population will grow from 4800 by 4800 x 1/3 = 1600
Hence, the population three years from now will be 4800 + 1600 = 6400.
Que 5: A man invests Rs.5000 for 3 years at 5% p.a. compound interest reckoned yearly. Income tax at the rate of 20% on the interest earned is deducted at the end of each year. Find the amount at the end of the third year.
(a) 5624.32
(b) 5630.50
(c) 5788.125
(d) 5627.20
Ans: Option 1
Sol: 5% is the rate of interest. 20% of the interest amount is paid as tax. That is 80% of the interest amount stays back. Therefore, if we compute the rate of interest as 80% of 5% = 4% p.a., we will get the same value.
The interest accrued for 3 years in compound interest = 3 x simple interest on principal + 3 x interest on simple interest + 1 x interest on interest on interest. = 3 x (200) + 3 x (8) + 1 x 0.32 = 600 + 24 + 0.32 = 624.32
The amount at the end of 3 years = 5000 + 624.32 = 5624.32
Amala, Bina, and Gouri invest money in the ratio of 3:4:5 in fixed deposits having respective annual interest rates in the ratio of 6:5:4. What is their total interest income (In Rs) After a year, will Bina's interest income exceed Amala's by Rs 250? [CAT PYQ]
Que 6: The difference between the compound interest and the simple interest on a certain sum at 12% p.a. for two years is Rs.90. What will be the value of the amount at the end of 3 years?
(a) 9000
(b) 6250
(c) 8530.80
(d) 8780.80
Ans: Option 4
Sol: The difference in the simple interest and compound interest for two years is on account of the interest paid on the first year's interest when interest is reckoned using compound interest, interest is compounded annually.
Hence 12% of simple interest = 90 => simple interest = 90/0.12 =750.
As the simple interest for a year = 750 @ 12% p.a., the principal = 750/0.12 = Rs.6250.
If the principal is 6250, then the amount outstanding at the end of 3 years = 6250 + 3(simple interest on 6250) + 3 (interest on simple interest) + 1 (interest on interest on
interest) = 6250 + 3(750) + 3(90) + 1(10.80) = 8780.80
Que 7: Vijay invested Rs.50,000 partly at 10% and partly at 15%. His total income after a year was Rs.7000. How much did he invest at the rate of 10%?
(a) Rs.40,000
(b) Rs.10,000
(c) Rs.12,000
(d) Rs.20,000
Ans: Option 2
Sol: The best way to solve this problem is by using the concept in Mixtures and Alligation.
Vijay earned a total income of Rs.7000 for his investment of 50,000.
Therefore, his average rate of return = 7000/50000 x 100
By rule of allegation, if the value of one of the products is 10 (cheaper) and the other is 15 (dearer) and if the two are mixed such that the average value of the mixture is 14 (mean price), then the two products have been mixed in the following ratio.
The ratio of
Cheaper product: Dearer product
(Dearer product price - mean price) : (Mean price - cheaper product price)
In our example, the cheaper product is the investment at 10%, the dearer product is the
investment at 15% and the mean price is the average return of 14%.
Therefore, the amount invested @10% interest = 1/5 x 50,000 = 10,000.
Que 8: A sum of money invested for a certain number of years at 8% p.a. simple interest grows to Rs.180. The same sum of money invested for the same number of years at 4% p.a. simple interest grows to Rs.120 only. For how many years was the sum invested?
(a) 25 years
(b) 40 years
(c) 33 years and 4 months
(d) Cannot be determined
Ans: Option 1
Sol:
From the information provided we know that,
Principal + 8% p.a. interest on principal for n years = 180 …….. (1)
Principal + 4% p.a. interest on principal for n years = 120 ……… (2)
Subtracting equation (2) from equation (1), we get
4% p.a. interest on principal for n years = Rs.60.
Now, we can substitute this value in equation (2),
i.e Principal + 60 = 120
= Principal = Rs.60.
We know that SI = pnr/100, where p is the principal, n the number of years and r the rate percent of interest.
In equation (2), p = Rs.60, r = 4% p.a. and the simple interest = Rs.60.
Therefore, 60 = (60 x n x 4)/100
=> n = 100/4 = 25 years.
Que 9: How long will it take for a sum of money to grow from Rs.1250 to Rs.10,000, if it is invested at 12.5% p.a simple interest?
(a) 8 years
(b) 64 years
(c) 72 years
(d) 56 years
Ans: Option 4
Sol:
Simple interest is given by the formula SI = (pnr/100), where p is the principal, n is the number of years for which it is invested, r is the rate of interest per annum
In this case, Rs. 1250 has become Rs.10,000.
Therefore, the interest earned = 10,000 – 1250 = 8750.
8750 = [(1250 x n x 12.5)/100]
=> n = 700 / 12.5 = 56 years.
Que 10: Rs. 5887 is divided between Shyam and Ram, such that Shyam's share at the end of 9 years is equal to Ram's share at the end of 11 years, compounded annually at the rate of 5%. Find the share of Shyam.
(a) 2088
(b) 2000
(c) 3087
(d) None of these
Ans: Option 3
Sol:
Shyam's share x (1+0.05)9 = Ram's share x (1 + 0.05)11
Shyam's share / Ram's share = (1 + 0.05)11 / (1+ 0.05)9 = (1+ 0.05)2 = 441/400
Therefore Shyam's share = (441/841) x 5887 = 3087.
Que 11: The question for the day is from the topic simple and compound interest. Shawn invested one-half of his savings in a bond that paid simple interest for 2 years and received Rs.550 as interest. He invested the remaining in a bond that paid compound interest, interest being compounded annually, for the same 2 years at the same rate of interest and received Rs.605 as interest. What was the value of his total savings before investing in these two bonds?
(a) Rs.5500
(b) Rs.1100
(c) Rs.2200
(d) Rs.2750
Ans: Option 4
Sol:
Shawn received an extra amount of (Rs.605 – Rs.550) Rs.55 on his compound interest paying bond as the interest that he received in the first year also earned interest in the second year.
The extra interest earned on the compound interest bond = Rs.55
The interest for the first year =550/2 = Rs.275
Therefore, the rate of interest =55/275 x 100 = 20% p.a.
20% interest means that Shawn received 20% of the amount he invested in the bonds as interest.
If 20% of his investment in one of the bonds = Rs.275, then his total investment in each of the bonds = 275/20 x 100 = 1375.
As he invested equal sums in both the bonds, his total savings before investing = 2 x 1375 = Rs.2750.
Que 12: Rs.100 doubled in 5 years when compounded annually. How many more years will it take to get another Rs.200 compound interest?
(a) 10 years
(b) 5 years
(c) 7.5 years
(d) 15 years
Ans: Option 2
Sol:
Rs.100 invested in compound interest becomes Rs.200 in 5 years.
The amount will double again in another 5 years.
i.e., the amount will become Rs.400 in another 5 years.
So, to earn another Rs.200 interest, it will take another 5 years.
Que 13: In the beginning of the year 2004, a person invests some amount in a bank. In the beginning of 2007, the accumulated interest is Rs.10,000 and in the beginning of 2010, the accumulated interest becomes Rs.25,000. The interest rate is compounded annually and the annual interest rate is fixed. The principal amount is _____:
(a) Rs.16,000
(b) Rs.18,000
(c) Rs.20,000
(d) Rs.25,000
Ans: Option 3
Sol:
Given Data
Interest from the start of 2004 to the start of 2007 (for 3 years) = Rs.10,000Interest from the start of 2004 to the start of 2010 (for 6 years) = Rs.25,000
Variables Assigned
Let the principal = x
And annual interest rate = 100r%
The formula to compute the Amount when a sum is invested in compound interest is given as follows:
Where A is the amount, P is the principal, r is the rate of interest per annum in % and n is the number of years
We have assigned x as the principal and 100r% as the rate of interest.∴ The amount for 3 years A3 =
= x(1 + r)3 = x + 10000 (Amount = Principal + Interest)
And amount for 6 years A3 = x(1 + r)6 = x + 25000
Further let us take, (1 + r)3 = a
Then, x(1 + r)3 = xa = x + 10000 ..... (1)
And x(1 + r)6 = xa2 = x + 25000 ..... (2)
Solve the two equations to find x
xa = x + 10000 ..... (1)
xa2 = x + 25000 ..... (2)
Bringing x terms to one side in both the equations, we can rewrite the two equations as
x(a – 1) = 10000
x(a2 – 1) = 25000
Equation (2) can therefore be expressed as x(a2 – 1) = x(a - 1) (a + 1) = 25000
We know from equation (1) x(a – 1) = 10000
Substitute x(a – 1) = 10000 in equation (2). ∴ x(a - 1) (a + 1) = 10000 (a + 1) = 25000
Or, (a + 1) = 25000/10000 = 2.5
If a + 1 = 2.5, a – 1 = (a + 1 – 2) = 2.5 – 2 = 0.5
From equation (1) we know x(a – 1) = 10000
We have computed (a – 1) = 0.5
So, x = 10000/0.5 = 20000.
A sum of money becomes 1.331 times in 3 years as compound interest. The rate of interest is
|
205 videos|264 docs|136 tests
|
FAQs on Interests: Solved Examples - CSAT Preparation - UPSC
| 1. What are the different types of interest commonly studied in finance? |  |
| 2. How is simple interest calculated? |  |
| 3. What is compound interest and how does it differ from simple interest? |  |
| 4. What factors influence the amount of interest accrued on an investment? |  |
| 5. How can understanding interest help in financial planning? |  |