Arithmetic Mean and Special Series | Mathematics (Maths) Class 11 - Commerce PDF Download
Arithmetic Mean
The sum of all of the numbers in a list divided by the number of terms in that list gives the arithmetic mean of that list. Let us first understand the concept of arithmetic progression.
In the arithmetic progression, we know that if the three numbers are in AP, that means if a, b and c are in AP, then basically the first two terms a and b will have the difference which will be equal to the next two terms b and c.
So we can say, b – a = c – b. Rearranging the terms,
2b = a + c
b = a+c/2
So we can say that this term b is the average of the other two terms a and c. This average in arithmetic progression is called the arithmetic mean.
Arithmetic mean = A = S/N
where A = arithmetic mean, N = the number of terms and S = the sum of the numbers in the list.

Multiple Arithmetics Means between Two Given Numbers
Let a and b be the two given numbers and A1, A2……An be the arithmetic means between them. Then a, A1, A2….An, b will be in AP. If a is the first term, then b will be the (n+2)th term.
Hence, b = a + (n + 2 – 1 )d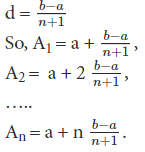
Geometric Mean
Geometric mean b of two terms a and c is given by √(ac). If a, b and c are in geometric progression, then the ratio of the two consecutive terms should be equal.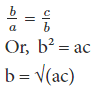
This means that b is the geometric mean of a and c
Multiple Geometric Means between Two Given Numbers
Let a and b be the two given numbers. Let, G1, G2, G3….Gn be n geometric mean between them.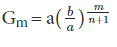
Example
Question: Insert 3 numbers between 1 and 256 so that the resulting sequence is GP
Solution: So we are supposed to insert three numbers, say
1 G1 G2 G3 256
Let’s insert these numbers in such a way that all these numbers are in G.P. We know that the general form of a GP is :a1, a1r, a1r², a1r³, a1rn-1, a1 rn … So, let us first write a = 1, G1 as ar, G2 as ar², and G3 = ar³. So,
a = 1 and ar4 = 256
or, r4 = (4)4
or, r = 4, -4
GP: 1 ar ar² ar³ 256
Case 1: r = 4
ar = 1 × 4
ar² = 1 × 4²
ar³ = 1 × 4³
GP: 1, 4, 16, 64, 256
Hence, 4, 16 and 64 are the three terms which we can add between 1 and 256.
Case 2: r = -4
ar = 1 × -4
ar² = 1 × -4²
ar³ = 1 ×-4³
GP: 1, -4, 16, -64, 256
Hence, -4, 16 and -64 are the three terms which we can add between 1 and 256.
Relationship between A.M and G.M
For terms a and b, let A be A.M and B be G.M, then A.M >= G.M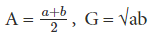
Let us take a = 5 and b = 5. In this case,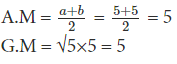
Here we see that A.M > G.M
So either A.M = G.M or A.M > G.M
Solved Examples
Question: Find the arithmetic mean of the series 1, 3, 5,……(2n-1)
A. n
B. 2n
C. n/2
D. n-1
Solution: A is the correct option. First term, a =1 and the common difference, d = 3 – 1 = 2. Let 2n – 1 b ethe kth term. Then, from the general term formula,
ak = a + (k-1)d
2n-1 = 1 + (k-1) 2
k-1 = n-1
or k =n
Now, Sk = [(k/2)*(2a+ (k-1)d]
And A.M = Sk/k = [2a + (k-1)d]/2
A.M = (2+(n-1)2)/2 = n
What is a Series?
We can define the series as the sum of all the numbers of the given sequence. The sequences are finite as well as infinite. In the same way, the series can also be I finite or infinite. For example, consider a sequence as 1, 3, 5, 7, … Then the series of these terms will be 1 + 3 + 5 + 7 + …
What are the Special Series?
The series special in some way or the other is called a special series. The following are the three types of special series.
• 1 + 2 + 3 +… + n (sum of first n natural numbers)
• 12 + 22 + 32 +… + n2(sum of squares of the first n natural numbers)
• 13 + 23 + 33 +… + n3(sum of cubes of the first n natural numbers)
Let’s now look at the sum to n terms of special series:
Sum of First n Natural Numbers (1 + 2 + 3 +… + n)
The above series is an AP. Here a = 1, d =1 because the difference between these terms is 1 and also 1st term is 1.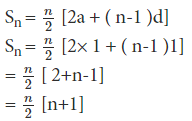
So above is the formula of the seies.
Sum of Squares of the First n Natural Numbers (12 + 22 + 32 +… + n2)
This series is neither in GP nor in AP. So let’s first convert this in GP or AP. Here we use the formula,
k3 – (k-1)3
= k3 – (k-1)3 = 3k2 – 3k +1
Let us take the value of k as k = 1
13 – 03 = 3 (1)2 – 3 (1) + 1
Now take k =2
23 – 13 = 3 (2)2 – 3 (2) + 1
Now k = 3
33 – 23 = 3(3)2 – 3 (3) + 1
Similarly if we take k =n, we get,
n3 – (n – 1)3 = 3 (n)2 – 3 (n) + 1
Now add both the sides, the equation we get is,
n3 – 03 = 3 (12 + 22 + 32 + … + n2) – 3 (1 + 2 + 3 + … + n) + n 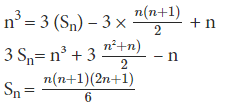
Sum of Cubes of the First n Natural Numbers (13 + 23 + 33 +… + n3)
Here we use the formula,
(k + 1)4 – k4 = 4k3 + 6k2 + 4k + 1
Let us take the value of k as k = 1
24 – 14 = 4(1)3 + 6(1)2 + 4(1) + 1
Now take the value of k = 2
34 – 24 = 4(2)3 + 6(2)² + 4(2) + 1
Again take k = 3
44 – 34 = 4(3)3 + 6(3)2 + 4(3) + 1
Similarly if we take k =n
(n + 1)4 – n4 = 4n3 + 6n2 + 4n + 1
Now adding both the sides, we get
(n + 1)4 – 14 = 4(13 + 23 + 33 +…+ n3) + 6(12 + 22 + 32 + …+ n2) + 4(1 + 2 +
3 +…+ n) + n
(n + 1)4 – 14 = 4 Sn + 6 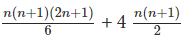 + n
+ n
= n4+ 4n³ + 6n² + 4n- n (2n² + 3n +1 )-2n(n+1)-n
= n4+ 2n³ + n²
= n² (n+1)² 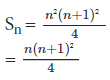
Hence we get the formula for all the three special cases.
Solved Examples
Question: 2, 3, 6, n, 42… Find the value of n in the above series.
A. 9
B. 12
C. 15
D. 18
E. 21
Solution: C is the correct option. Given series is 2, 3, 6, n, 42… Here we can decode the series by multiplying the previous number by 3 and then by subtracting 3 from it. As we can see 2 being the first numbers of the series.
2 × 3 = 6
6 – 3 = 3 (3 is the second number)
3 × 3 -3 = 6 ( 6 is the third number)
n will be 6 × 3 – 3 = 18-3 = 15
Hence, n is 15
Question: Consider the following statements:
(1) The sum of cubes of first 2o natural numbers is 44400
(2) The sum of squares of first 20 natural numbers is 2870
Which of the above statements is/are correct?
Only 1st
Only 2nd
Solution: B is the correct option. The sum of the cubes of first n consecutive natural
numbers is given by 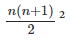
Putting n = 20, we have sum = 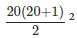 = 44100
= 44100
The sum of the squares of first n consecutive natural numbers is given by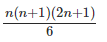
Putting n = 20, we have the sum = 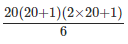 = 2870
= 2870
|
74 videos|245 docs|91 tests
|
FAQs on Arithmetic Mean and Special Series - Mathematics (Maths) Class 11 - Commerce
| 1. What is the arithmetic mean and how is it calculated? |  |
| 2. How is the arithmetic mean useful in analyzing data? |  |
| 3. What are the limitations of using the arithmetic mean? |  |
| 4. How is the arithmetic mean different from the median and mode? |  |
| 5. Can the arithmetic mean be used with non-numeric data? |  |


















