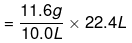NCERT Solutions Class 11 Chemistry Chapter 1 - Basic Concepts of Chemistry
Q.1.23. In a reaction A + B2 → AB2
Identify the limiting reagent, if any, in the following reaction mixtures.
(a) 300 atoms of A + 200 molecules of B2
(b) 2 mol A + 3 mol B2
(c) 100 atoms of A + 100 molecules of B2
(d) 5 mol A + 2.5 mol B
(e) 2.5 mol A + 5 mol B
Ans. A limiting reagent determines the extent of a reaction. It is the reactant which is the first to get consumed during a reaction, thereby causing the reaction to stop and limiting the amount of products formed.
(a) According to the given reaction, 1 atom of A reacts with 1 molecule of B. Thus, 200 molecules of B will react with 200 atoms of A, thereby leaving 100 atoms of A unused. Hence, B is the limiting reagent.
(b) According to the reaction, 1 mol of A reacts with 1 mol of B. Thus, 2 mol of A will react with only 2 mol of B. As a result, 1 mol of A will not be consumed. Hence, B is the limiting reagent.
(c) According to the given reaction, 1 atom of A combines with 1 molecule of B. Thus, all 100 atoms of A will combine with all 100 molecules of B. Hence, the mixture is stoichiometric where no limiting reagent is present.
(d) 1 mol of atom A combines with 1 mol of molecule B. Thus, 2.5 mol of B will combine with only 2.5 mol of A. As a result, 2.5 mol of A will be left as such. Hence, B is the limiting reagent.
(e) According to the reaction, 1 mol of atom A combines with 1 mol of molecule B. Thus, 2.5 mol of A will combine with only 2.5 mol of B and the remaining 2.5 mol of B will be left as such. Hence, A is the limiting reagent.
Q.1.24. Dinitrogen and dihydrogen react with each other to produce ammonia according to the following chemical equation:
N2(g) + H2(g) → 2NH3(g)
(a) Calculate the mass of ammonia produced if 2.00 × 103 g dinitrogen reacts with 1.00 × 103 g of dihydrogen.
(b) Will any of the two reactants remain unreacted?
(c) If yes, which one and what would be its mass?
Ans.
(a) Balancing the given chemical equation,
N2(g) + H2(g) → 2NH3(g)
From the equation, 1 mole (28 g) of dinitrogen reacts with 3 mole (6 g) of dihydrogen to give 2 mole (34 g) of ammonia.
⇒ 2.00 × 103 g of dinitrogen will react with 6 g/28 g × 2.00 x 103 g dihydrogen i.e., 2.00 × 103 g of dinitrogen will react with 428.6 g of dihydrogen.
Given,
Amount of dihydrogen = 1.00 × 103 g
Hence, N2 is the limiting reagent. 28 g of N2 produces 34 g of NH3.
Hence, mass of ammonia produced by:
2000 g of N2 = 34 g/28 g × 2000g
= 2428.57 g
(b) N2 is the limiting reagent and H2 is the excess reagent. Hence, H2 will remain unreacted.
(c) Mass of dihydrogen left unreacted = 1.00 × 103 g – 428.6 g = 571.4 g
Q.1.25. How are 0.50 mol Na2CO3 and 0.50 M Na2CO3 different?
Ans.
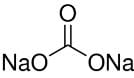
Molar mass of Na2CO3 = (2 × 23) +12.00 + (3 × 16) = 106 g mol–1
Now, 1 mole of Na2CO3 means 106 g of Na2CO3.
⇒ 0.5 mol of Na2CO3
= 53 g Na2CO3
⇒ 0.50 M of Na2CO3 = 0.50 mol/L Na2CO3
Hence, 0.50 mol of Na2CO3 is present in 1 L of water or 53 g of Na2CO3 is present in 1 L of water.
Q.1.26. If ten volumes of dihydrogen gas react with five volumes of dioxygen gas, how many volumes of water vapour would be produced?
Ans. Reaction of dihydrogen with dioxygen can be written as:
2H2(g) + O2(g) → 2H2O(g)
Now, two volumes of dihydrogen react with one volume of dihydrogen to produce two volumes of water vapour.
Hence, ten volumes of dihydrogen will react with five volumes of dioxygen to produce ten volumes of water vapour.
Q.1.27. Convert the following into basic units:
(a) 28.7 pm
(b) 15.15 pm
(c) 25365 mg
Ans.
(a) 28.7 pm
1 pm = 10–12 m
28.7 pm = 28.7 × 10–12 m
= 2.87 × 10–11 m
(b) 15.15 pm
1 pm = 10–12 m
15.15 pm = 15.15 × 10–12 m
= 1.515 × 10–11 m
(c) 25365 mg
1 mg = 10–3 g
25365 mg = 2.5365 × 104 × 10–3 g
Since,
1 g = 10–3 kg
2.5365 × 101 g = 2.5365 × 10–1 × 10–3 kg
25365 mg = 2.5365 × 10–2 kg.
Q.1.28. Which one of the following will have largest number of atoms?
(a) 1 g Au (s)
(b) 1 g Na (s)
(c) 1 g Li (s)
(d) 1 g of Cl2(g)
Ans.
(a) 1 g of Au (s)
= 1/197 mol of Au (s) = 6.022 × 1023/197
atoms of Au (s) = 3.06 × 1021 atoms of Au (s)
(b) 1 g of Na (s) = 1/23 mol of Na (s)
= 6.022 × 1023/23 atoms of Na (s)
= 0.262 × 1023 atoms of Na (s)
= 26.2 × 1021 atoms of Na (s)
(c) 1 g of Li (s) = 1/7 mol of Li (s)
= 6.022 × 1023/7 atoms of Li (s)
= 0.86 × 1023 atoms of Li (s)
= 86.0 × 1021 atoms of Li (s)
(d) 1 g of Cl2 (g) = 1/71 mol of Cl2 (g)
(Molar mass of Cl2 molecule = 35.5 × 2 = 71 g mol–1)
= 6.022 x 1023/71
= 0.0848 × 1023 molecules of Cl2 (g)
= 8.48 × 1021 molecules of Cl2 (g)
As one molecule of Cl2 contains two atoms of Cl.
Number of atoms of Cl = 2 × 8.48 × 1021 =16.96 × 1021 atoms of Cl
Hence, 1 g of Li (s) will have the largest number of atoms.
Q.1.29. Calculate the molarity of a solution of ethanol in water in which the mole fraction of ethanol is 0.040 (assume the density of water to be one).
Ans. Mole fraction of C2H5OH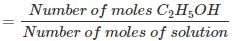
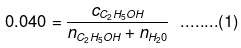
Number of moles present in 1 L water:
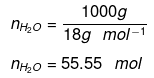
Substituting the value of nH2O in equation (1)
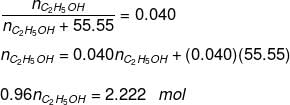
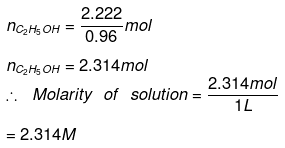
Q.1.30. What will be the mass of one 12C atom in g?
Ans. 1 mole of carbon atoms = 6.023 × 1023 atoms of carbon
= 12 g of carbon
Mass of one 12C atom = 12 g/6.022 × 1023
= 1.993 × 10–23 g.
Q.1.31. How many significant figures should be present in the of the following calculations?
(a)
(b) 5 × 5.364
(c) 0.0125 + 0.7864 + 0.0215
Ans.
(a)
Least precise number of calculation = 0.112
Number of significant figures in the Ans:
= Number of significant figures in the least precise number
= 3
(b) 5 × 5.364
Least precise number of calculation = 5.364
Number of significant figures in the Ans: = Number of significant figures in 5.364 = 4
(c) 0.0125 + 0.7864 + 0.0215
Since the least number of decimal places in each term is four, the number of significant figures in the Ans: is also 4.
Q.1.32. Use the data given in the following table to calculate the molar mass of naturally occurring argon isotopes:
Ans. Molar mass of argon:
= 39.947 g mol–1
Q.1.33. Calculate the number of atoms in each of the following
(a) 52 moles of Ar
(b) 52 u of He
(c) 52 g of He.
Ans.
(a) 1 mole of Ar = 6.022 × 1023 atoms of Ar
52 mol of Ar = 52 × 6.022 × 1023 atoms of Ar
= 3.131 × 1025 atoms of Ar
(b) 1 atom of He = 4 u of He
Or,
4 u of He = 1 atom of He
1 u of He= 1/4 atom of He
52 u of He = 52 /4 atoms of He
= 13 atoms of He
(c) 4 g of He = 6.022 × 1023 atoms of He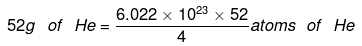
= 7.8286 × 1024 atoms of He.
Q.1.34. A welding fuel gas contains carbon and hydrogen only. Burning a small sample of it in oxygen gives 3.38 g carbon dioxide, 0.690 g of water and no other products. A volume of 10.0 L (measured at STP) of this welding gas is found to weigh 11.6 g.
Calculate:
(a) empirical formula
(b) molar mass of the gas
(c) molecular formula.
Ans.
(a) 1 mole (44 g) of CO2 contains 12 g of carbon.
3.38 g of CO2 will contain carbon = 12 g/44 g × 3.38 g = 0.9217 g
18 g of water contains 2 g of hydrogen. = 2 g/18 g × 0.690
0.690 g of water will contain hydrogen = 0.0767 g
Since carbon and hydrogen are the only constituents of the compound, the total mass of the compound is:
= 0.9217 g + 0.0767 g
= 0.9984 g
Percent of C in the compound = 0.9217 g/0.9984 × 100
= 92.32%
Percent of H in the compound = 0.0767 g/0.9984 × 100
= 7.68%
Moles of carbon in the compound = 92.32/12.00
= 7.69
Moles of hydrogen in the compound = 7.68
∴ Ratio of carbon to hydrogen in the compound = 7.69 : 7.68
= 1: 1
Hence, the empirical formula of the gas is CH.
(b) Given,
Weight of 10.0 L of the gas (at S.T.P) = 11.6 g
∴ Weight of 22.4 L of gas at STP
= 25.984 g
≈ 26 g.
Hence, the molar mass of the gas is 26 g.
(c) Empirical formula mass of CH = 12 + 1 = 13 g
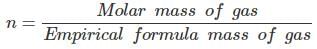
= 26 g/13 g
n = 2
Molecular formula of gas = (CH) = C2H2
Q.1.35. Calcium carbonate reacts with aqueous HCl to give CaCl2 and CO2 according to the reaction,
CaCO3(s) + 2HCl(aq) → CaCl2(aq) + CO2(g) + H2O(l)
What mass of CaCO3 is required to react completely with 25 mL of 0.75 M HCl?
Ans.
0.75 M of HCl
≡ 0.75 mol of HCl are present in 1 L of water
≡ [(0.75 mol) × (36.5 g mol–1)] HCl is present in 1 L of water
≡ 27.375 g of HCl is present in 1 L of water
Thus, 1000 mL of solution contains 27.375 g of HCl.
Amount of HCl present in 25 mL of solution
= 27.375 g/1000 mL × 25 mL
= 0.6844 g
From the given chemical equation,
CaCO3(g) + 2HCl(aq) → CaCl2(aq) + CO2(g) + H2O(l)
2 mol of HCl (2 × 36.5 = 73 g) react with 1 mol of CaCO3 (100 g).
∴ Amount of CaCO3 that will react with 0.6844 g = (100/73) × 0.6844
= 0.9375 g
Q.1.36. Chlorine is prepared in the laboratory by treating manganese dioxide (MnO2) with aqueous hydrochloric acid according to the reaction
4 HCl(aq) + MnO2(s) → 2 H2O(l) + MnCl2(aq) + Cl2(g)
How many grams of HCl react with 5.0 g of manganese dioxide?
Ans. 1 mol [55 + 2 × 16 = 87 g] MnO2 reacts completely with 4 mol [4 × 36.5 = 146 g] of HCl.
5.0 g of MnO2 will react with
= 146 g/87 g × 5.0 g of HCl
= 8.4 g of HCl
Hence, 8.4 g of HCl will react completely with 5.0 g of manganese dioxide.
|
22 videos|163 docs|17 tests
|
FAQs on NCERT Solutions Class 11 Chemistry Chapter 1 - Basic Concepts of Chemistry
| 1. What are the basic concepts of chemistry? |  |
| 2. How can I prepare for JEE Chemistry? |  |
| 3. What is the importance of understanding basic concepts in Chemistry for JEE? |  |
| 4. How can I improve my understanding of Chemistry concepts? |  |
| 5. Are NCERT Solutions sufficient for JEE Chemistry preparation? |  |