Acceleration: Applications, Formulas & Problems | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download

What is Acceleration?

It is the rate of change of velocity with time. The only two ways to accelerate is by changing the speed or change in direction or change both. It is a vector quantity. If the velocity of the object increases with time, its acceleration increases. If the velocity of an object decreases with time, its acceleration is negative.

The motion is uniformly accelerated motion or it non-uniformly accelerated, depending on how the velocity changes with time. It is uniform for a body if the velocity changes by equal amounts in equal intervals and if its velocity changes by unequal amounts, it is non-uniform.

Acceleration=  Change in velocity/time taken

Its unit is m/s²

Constant speed does not guarantee that acceleration is zero. For example, a body moving with constant speed in a circle changes its velocity every instant and hence its acceleration is not equal to zero.

Velocity is a quantity having both magnitude and direction, a change in velocity may involve either or both of these factors. Acceleration may result from a change in speed, a change in direction or changes in both. Like velocity, acceleration can also be positive, negative or zero.

Acceleration Formula

Acceleration is a measure of how quickly the velocity of an object changes. So, the acceleration is the change in the velocity, divided by the time. Acceleration has a magnitude (a value) and a direction. The direction of the acceleration does not have to be the same as the direction of the velocity. The units for acceleration are meters per second squared (m/s²).

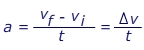
a = acceleration (m/s²)

vf = the final velocity (m/s)

vi = the initial velocity (m/s)

t = the time in which the change occurs (s)

Δv = short form for "the change in" velocity (m/s)

Classification of Motion in Straight Line 

Uniform Motion

This type of motion is defined as the motion of an object in which the object travels in a straight line and its velocity remains constant along that line as it covers equal distances in equal intervals of time, irrespective of the duration of the time.

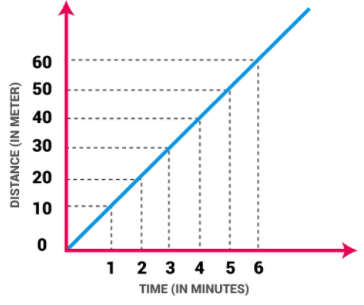
If a body is involved in rectilinear motion and the motion is consistent, then the acceleration of the body must be zero.

Example of Uniform Motion:

(i) If the speed of a car is 10 m/s, it means that the car covers 10 meters in one second. The speed is constant in every second.
(ii) Movement of blades of a ceiling fan.

Non Uniform Motion

This type of motion is defined as the motion of an object in which the object travels with varied speed and it does not cover same distance in equal time intervals, irrespective of the time interval duration.

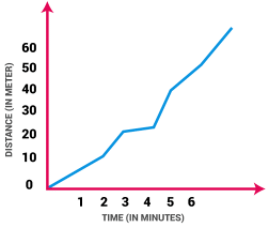
If a body is involved in rectilinear motion, and if the motion is not consistent, then the acceleration of the body must be non-zero.

Example of Non Uniform Motion:

(i) If a car covers 10 meters in first two seconds, and 15 meters in next two seconds.

(ii) The motion of a train.

Now, people usually get confused between uniform motion and uniform acceleration. In the later phenomena, the object is having a constant acceleration in rectilinear motion, which means the object has different speed in every second, which clearly defines that motion is changing.

Motion in Different Acceleration for Different Time Intervals

Let’s understand this through an example. Suppose, a particle started its motion from rest with an acceleration of 1m/s² for 2s and then continued it for next 1s changing to 2m/s². The distance travelled during this will be:

After 2s the velocity is, v = u+at = 2 m/s

Now, if this is the initial velocity for the second half of the motion, s2=ut+(1/2)at² =3 m

Distance traveled in first half is: s₁ = 0+(1/2)at² = 2 m

Hence total distance traveled = s₁+s₂ = 5 m

Average Acceleration

It is the change in velocity divided by an elapsed time. For instance, if the velocity of a marble increases from 0 to 60 cm/s in 3 seconds, its average acceleration would be 20 cm/s². This means that the marble’s velocity will increase by 20 cm/s every second.

It is the rate of change of velocity with respect to displacement

Acceleration is a = dv/dt

∴ a = dv/(dx/v)

a = v(dv/dx)

Freefall object experiences an acceleration of g= 9.8m/s² in a downward direction that is towards the center of the earth. In upward direction it is -g = -9.8m/s²

Acceleration of the Velocity-Time graph

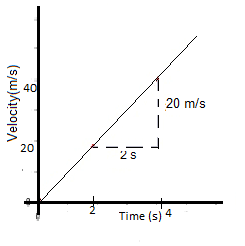
In the given graph, a =  (40-20)/(4-2) = 10 m/s². For a particle it is equal to the slope of a velocity-time graph.

Solved Example:

A. Zero

B. 10m/s² downward

C. 15m/s² upward

D. 15m/s² downward

Answer: B. A body in the air always experiences a gravitational force in a downward direction. Thus the body is in the downward direction with a constant magnitude.

Q. A sports car is travelling at a constant velocity v = 5.00 m/s. The driver steps on the gas, and the car accelerates forward. After 10.0 seconds, the driver stops accelerating and maintains a constant velocity v = 25.0 m/s. What was the car’s acceleration?
Answer: The initial velocity is v_i = 5.00 m/s, in the forward direction. The final velocity is v_f = 25.0 m/s in the forward direction. The time in which this change occurred is 10.0 s. The acceleration is in the forward direction, with a value:

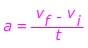
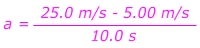
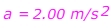
The car's acceleration is 2.00 m/s², forward.

Q. A child drops a rock off of a cliff. The rock falls for 15.0 s before hitting the ground. The acceleration due to gravity is g = 9.80 m/s2. What was the velocity of the rock the instant before it hit the ground?
Answer: The rock was released from rest, so the initial velocity is vi = 0.00 m/s. The time in which the change occurred is 15.0 s. The acceleration is 9.80 m/s². The final velocity must be found, so rearrange the equation: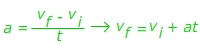

v_f = v_i + at
v_f = 0.00 m/s +(9.80 m/s²)(15.0 s)
v_f = 147 m/s
The rock is falling, so the direction of the velocity is down.