The Solenoid and the Toroid - NEET PDF Download
| Table of contents |
|
| Solenoid |
|
| Amperian Loop to Determine the Magnetic Field |
|
| A long solenoid |
|
| Toroid |
|
| Solved Examples For You |
|
Solenoid
The solenoid is a coil of wire that acts like an electromagnet when a flow of electricity passes through it. Electromagnetic solenoids find uses all over the world. You can hardly swing a bat without hitting a solenoid.Speakers and microphones both contain solenoids. In fact, a speaker and microphone are pretty much exactly the same things in reverse of each other.
Amperian Loop to Determine the Magnetic Field
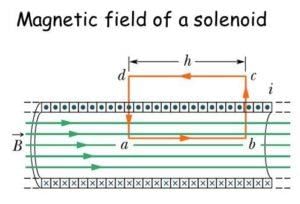
Consider an Amperian loop with sides abcd and integrate along each side. In bc and da, the field is perpendicular to dl. Along cd, the field is zero. Along transverse sections bc and ad, the field component is zero. Thus, these two sections make no contribution. Let the field along ab be B. Thus, the relevant length of the Amperian loop is, L = h.
Let n be the number of turns per unit length, then the total number of turns is nh. The enclosed current Ie = I (nh), where I is the current in the solenoid.
BL = μ0Ie, Bh = μ0I(nh)
B = μ0nI
The direction of the field is given by the right-hand rule. The solenoid is commonly used to obtain a uniform magnetic field.
A long solenoid
A long solenoid is the one which has a larger length in comparison to the radius. It consists of a long wire wound in the form of a helix where the neighbouring turns are closely spaced. So each turn can be regarded as a circular loop. The net magnetic field is the vector sum of the fields due to all the turns. Enamelled wires are used for winding so that turns are insulated from each other.
The magnetic field inside a long solenoid is: B = μo nI ……….(1) where n = number of turns per unit length and I = current flowing through the solenoid. The magnetic field at a point on one end of the long solenoid is:
B = (μo nI / 2) ……….(2)
Toroid
A toroid is a coil of insulated or enameled wire wound on a donut-shaped form made of powdered iron. low-level inductors, power inductors, low-level transformers, current transformers and power transformers are some of the applications of Toroid.
Toroid
A toroid is an endless solenoid in the form of a ring. The magnetic field inside a toroid is given as,
B = (μoNI / 2πr) ……….(3)
where I = current flowing through the solenoid. Let r be the average radius of the toroid and n be the number of turns per unit length and N = 2πrn = (average) perimeter of the toroid × number of turns per unit length. On comparing the two results: for a solenoid and toroid. Equations (1) and (3) will give, we get B = μ0 n I, i.e., the result for the solenoid.
Solved Examples For You
Question: A long solenoid is fabricated to closely winding wire of radius 0.5mm over a cylinderical frame, so that the successive turns nearly touch each other. The magnetic field at the centre of solenoid, if it carries a current of 5A is?
A) 4π × 10-2 T B) 2π × 10-3 T C) 5π × 10-4 T D) 4π × 10-5 T
Solution:
The turns of wire on the solenoid are shown in figure.
Number of turns in 1
mm = 1, n = 1000 turns / m
Therefore, B = μ0nI = 4π × 10−7 × 103 × 5 = 2π × 10−3 T
Previous Year Questions with Solutions
,Viva Questions
,ppt
,study material
,video lectures
,Exam
,The Solenoid and the Toroid - NEET
,Summary
,Objective type Questions
,Important questions
,mock tests for examination
,The Solenoid and the Toroid - NEET
,shortcuts and tricks
,MCQs
,The Solenoid and the Toroid - NEET
,Free
,past year papers
,Extra Questions
,practice quizzes
,Semester Notes
,Sample Paper
;
The Solenoid and the Toroid Free PDF Download
Importance of The Solenoid and the Toroid
The Solenoid and the Toroid Notes
The Solenoid and the Toroid NEET Questions
Study The Solenoid and the Toroid on the App
|
© EduRev
|
Education Revolution
|
|
