DC Pandey Solutions: Motion in One Dimension- 3 | DC Pandey Solutions for JEE Physics PDF Download
Introductory Exercise 3.3
Ques 1: Figure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t = t1 and t = t2.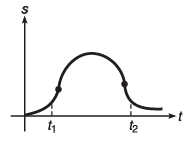
Ans: vt1, at1 and at2 are positive while vt2 is negative
Sol: At t = t1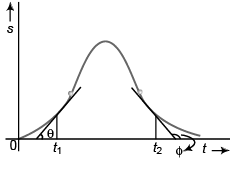
v = tan θ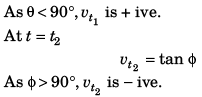
Corresponding v-t graph will be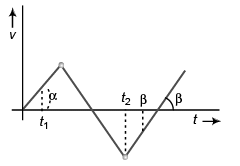
Acceleration at t = t1 : 
As α < 90°, a t1 is + ive constant.
Acceleration at t = t2
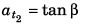
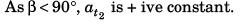
Ques 2: A particle of mass m is released from a certain height h with zero initial velocity. It strikes the ground elastically (direction of its velocity is reversed but magnitude remains the same). Plot the graph between its kinetic energy and time till it returns to its initial position.
Ans:
Sol: Let the particle strike ground at time t velocity of particle when it touches ground
would be gt. KE of particle will be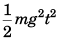 i.e., KE ∝ t2. While going up the velocity will get - ive but the KE will remain. KE will reduce to zero at time 2 t when the particle reaches its initial position.
i.e., KE ∝ t2. While going up the velocity will get - ive but the KE will remain. KE will reduce to zero at time 2 t when the particle reaches its initial position.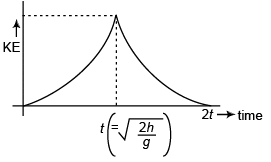

Ques 3: A ball is dropped from a height of 80 m on a floor. At each collision, the ball loses half of its speed. Plot the speed-time graph and velocity-time graph of its motion till two collisions with the floor. [Take g = 10 m/s2]
Ans: 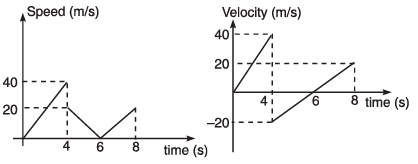
Sol: Speed of ball (just before making first collision with floor) 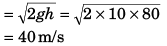
Time taken to reach ground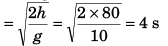
Speed of ball (just after first collision with floor)
= 40/2 = 20 m/s
Time to attain maximum height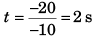
∴ Time for the return journey to floor = 2 s.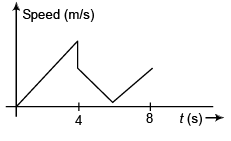
Corresponding velocity-time will be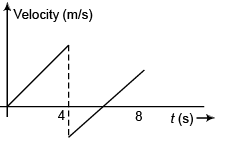
Ques 4: Figure shows the acceleration-time graph of a particle moving along a straight line. After what time the particle acquires its initial velocity?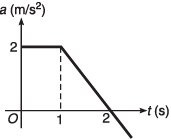
Ans: (2 + √3) s
Sol: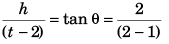
⇒ h = 2 (t - 2)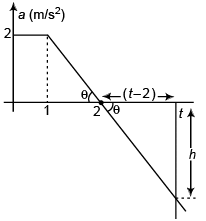
Particle will attain its initial velocity i.e., net increase in velocity of the particle will be zero when,
area under a-t graph = 0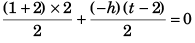
or 3 - (t - 2)2 = 0
or (t - 2)2 = 3
or t - 2 = ± √3
or t = 2 ± √3
At time t = 2 + √3 s
Introductory Exercise 3.4
Ques 1: Two balls A and B are projected vertically upwards with different velocities. What is the relative acceleration between them?
Ans: zero
Sol: Relative acceleration of A w.r.t. B
αAB = (+ g) - (+ g) = 0
Ques 2: In the above problem what is the shape of the graph between distance between the balls and time before either of the two collide with ground?
Ans: straight line passing through origin
Sol: Velocity of A w.r.t. B = vA - vB
∴ Relative displacement (i.e., distance between A and B) would be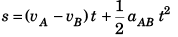
or s = (vA - vB) t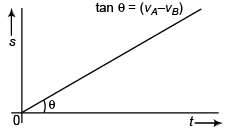
Ques 3: A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10.0 m/s with respect to the water in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?
Ans: (a) 40 s
(b) 80 m
Sol: In figure, u = speed of boat
v = speed of river flow
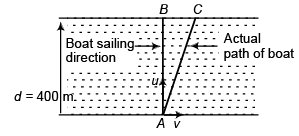
Time to cross river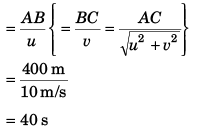
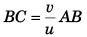
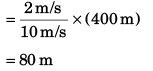
Ques 4: An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. Wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s.
(a) Find the direction in which the pilot should head the plane to reach the point B.
(b) Find the time taken by the plane to go from A to B.
Ans: 
(b) 50 min
Sol: Let C be the point along which pilot should head the plane.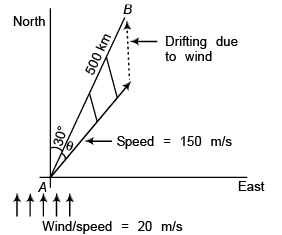
Apply sine formula in Δ ABC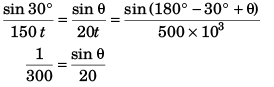
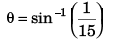
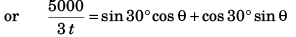
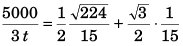
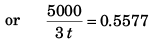
⇒ 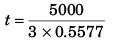
= 2989 s
= 50 min
Ques 5: Two particles A and B start moving simultaneously along the line joining them in the same direction with acceleration of 1 m/s2 and 2 m/s2 and speeds 3 m/s and 1 m/s respectively. Initially A is 10 m behind B. What is the minimum distance between them?
Ans: 8 m
Sol: αA = 1 m/s2 , αB = 2 m/s2
vA = 3 m/s, vB = 1 m/s
Acceleration of A w.r.t. B = 1 - 2 = - 1 m/s2
Velocity of A w.r.t. B = 3 - 1 = 2 m/s
Initial displacement of A w.r.t. B = - 10 m
At time relative displacement of A w.r.t. B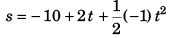
or s = - 10 + 2t - 0.5t2
For s to be minimum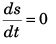
or 2 - (0.5 x 2t) = 0
i.e., t = 2 s
∴ smin = - 10 + (2 x 2) - 0.5 x (2)2
= - 10 + 4 - 2
= - 8 m
Minimum distance between A and B = 8 m.
FAQs on DC Pandey Solutions: Motion in One Dimension- 3 - DC Pandey Solutions for JEE Physics
| 1. What is motion in one dimension? |  |
| 2. How is displacement different from distance in one-dimensional motion? |  |
| 3. What is the difference between speed and velocity in one-dimensional motion? |  |
| 4. What is meant by uniform motion in one dimension? |  |
| 5. How is acceleration related to velocity in one-dimensional motion? |  |





















