DC Pandey Solutions (JEE Main): Mechanics of Rotational Motion- 1 | DC Pandey Solutions for JEE Physics PDF Download
Subjective Questions
Moment of inertia
Ques 1: Four thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
Ans: 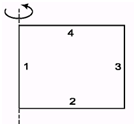
I = I1 + I2 + I3 + I4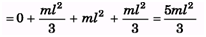
Ques 2: A mass of 1 kg is placed at (1 m, 2 m, 0). Another mass of 2 kg is placed at (3 m, 4 m, 0). Find moment of inertia of both the masses about z-axis.
Ans: I = I1 + I2
= 1 × (12 + 22) + 2(32 + 42) = 55 kg-m2
Ques 3: Moment of inertia of a uniform rod of mass m and length l is 7/12 ml2 about a line perpendicular to the rod.
Find the distance of this line from the middle point of the rod.
Ans: 
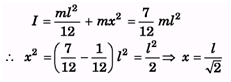
Ques 4: Find the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals.
Ans: 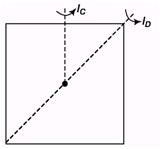
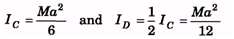
Ques 5: Radius of gyration of a body about an axis at a distance 6 cm from its centre of mass is 10 cm. Find its radius of gyration about a parallel axis through its centre of mass.
Ans: 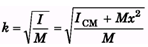
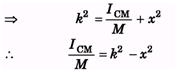
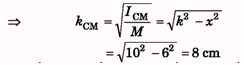
Ques 6: Two point masses m1 and m2 are joined by a weightless rod of length r. Calculate the moment of inertia of the system about an axis passing through its centre of mass and perpendicular to the rod.
Ans: 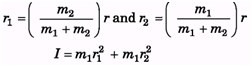
Substituting the values we get,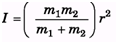
Ques 7: Linear mass density (mass/length) of a rod depends on the distance from one end (say λ) as λx = (αx + b). Here, α and β are constants. Find the moment of inertia of this rod about an axis passing through A and perpendicular to the rod. Length of the rod is l.
Ans: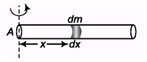
dI = dmx2 = x2λdx = x2(αx + β)dx
(αx3 + βx2) dx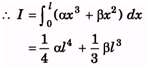
Angular Velocity
Ques 8: Find angular speed of second's clock.
Ans: In second's clock, it takes 60 s by the seconds hand to rotate by 2π.
So, 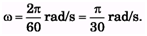
Ques 9: A particle is located at (3 m, 4 m) and moving with 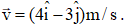
Find its angular velocity about origin at this instant.
Ans: 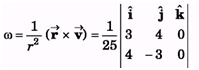
Ques 10: Particle P shown in figure is moving in a circle of radius R = 10cm with linear speed v = 2m/s. Find the angular speed of particle about point O.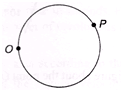
Ans: 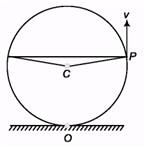
ωc = 2ωo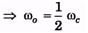
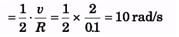
Ques 11: Two points P and Q, diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc.
Ans: 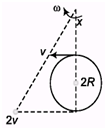
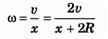
⇒ x + 2R=2x
⇒ x=2R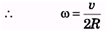
Ques 12. Point A of rod AB(l = 2m)is moved upwards against a wall with velocity v = 2m/s. Find angular speed of the rod at an instant when θ = 60°.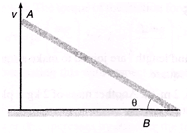
Ans: 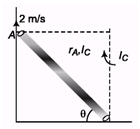
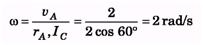
Torque
Ques 13: A force 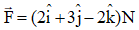 is acting on a body at point (2 m, 4 m, -2 m). Find torque of this force about origin.
is acting on a body at point (2 m, 4 m, -2 m). Find torque of this force about origin.
Ans: 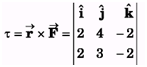
= i (- 8 + 6) - j (- 4 + 4) + k (6 - 8)
= -2i - 2k = -2(i + k)Nm
Ques 14: A particle of mass m = 1 kg is projected with speed u=20√2m/s at angle θ = 45° with horizontal Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
Ans: 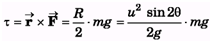
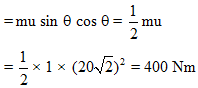
Ques 15: Point C is the centre of mass of the rigid body shown in figure. Find the total torque acting on the body about point C.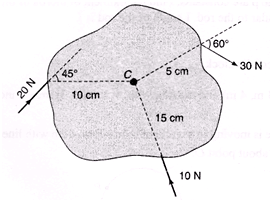
Ans: τ = τ10 + τ20 + τ30
= 0 + 20 sin 45° × 0.1 + 30 sin 60° × 0.05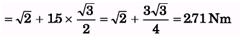
Ques 16: Find the net torque on the wheel in figure about the point O if a = 10 cm and b = 25 cm.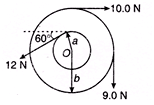
Ans: τ = 12 cos 60° × 0.1 - 10 × 0.25 - 9 × 0.25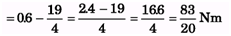
Rotation of a Rigid Body About a Fixed Axis Uniform angular acceleration
Ques 17: A wheel rotating with uniform angular acceleration covers 50 rev in the first five seconds after the start. Find the angular acceleration and the angular velocity at the end of five seconds.
Ans: 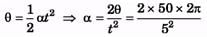
= 8π rad/s2
w = αt = 8π rad/s2 × 5s = 40 rad/s
Ques 18: A wheel starting from rest is uniformly accelerated with a = 2 rad/s2 for 5 s. It is then allowed to rotate uniformly for the next two seconds and is finally brought to rest in the next 5 s. Find the total angle rotated by the wheel.
Ans: θ = θ1 + θ2 + θ3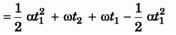
α t1 (t1 + t2) = 2 × 5(5 + 2) = 70rad
Ques 19: A wheel whose moment of inertia is 0.03 kg m2, is accelerated from rest to 20 rad/s in 5 s. When the external torque is removed, the wheel stops in 1 min. Find:
(a) the frictional torque,
(b) the external torque
Ans: ω1 = α1t1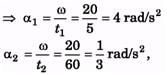
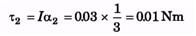
is the torque due to friction. Again,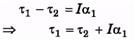
or τ1 = 0.01 + 0.03 × 4 = 0.13 Nm
Ques 20: A body rotating at 20 rad/s is acted upon by a constant torque providing it a deceleration of 2rad/s2. At what time will the body have kinetic energy same as the initial value if the torque continues to act ?
Ans: ω = ω0 + αt
⇒ - 20 rad/s
= 20 rad/s - 2 rad/s2 × t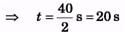
Ques 21: A uniform disc of mass 20 kg and radius 0.5 m can turn about a smooth axis through its centre and perpendicular to the disc. A constant torque is applied to the disc for 3 s from rest and the angular velocity at the end of that time is 240/π rev/min. Find the magnitude of the torque. If the torque is then removed and the disc is brought to rest in t seconds by a constant force of 10 N applied tangentially at a point on the rim of the disc, find t.
Ans: 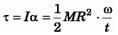
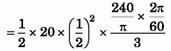
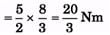
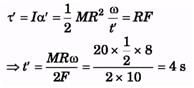
Q 22. A uniform disc of mass m and radius R is rotated about an axis passing through its centre and perpendicular to its plane with an angular velocity w0. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is m.
Find:
(a) the time when disc stops rotating,
(b) the angle rotated by the disc before stopping.
Ans: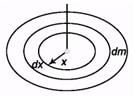
(a) dτ =μ.dm.g.x 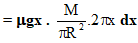
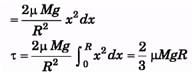
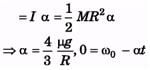
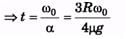
(b) 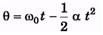
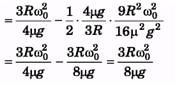
Non-uniform angular acceleration
Ques 23:A flywheel whose moment of inertia about its axis of rotation is 16 kg-m2 is rotating freely in its own plane about a smooth axis through its centre. Its angular velocity is 9 rad s-1 when a torque is applied to bring it to rest in t0 seconds. Find t0 if:
(a) the torque is constant and of magnitude of 4 Nm,
(b) the magnitude of the torque after t seconds is given by kt.
Ans:
(a) τ = Iα and 0 = ω0 - αt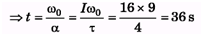
(b) 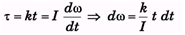
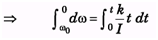
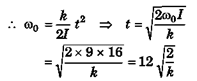
Ques 24: A shaft is turning at 65 rad/s at time zero. Thereafter, angular acceleration is given by α = -10 rad/s2 - 5t rad/s2. where t is the elapsed time.
(a) Find its angular speed at t = 3.0s.
(b) How far does it turn in these 3s ?
Ans: 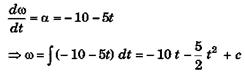
at t = 0, ω= c = 65 rad/s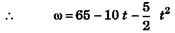
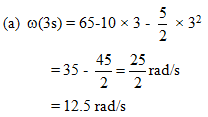
(b) 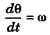
⇒ dθ = ωdt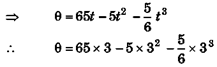
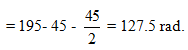
Ques 25: The angular velocity of a gear is controlled according to ω = 12 - 3t2 where ω, in radian per second, is positive in the clockwise sense and t is the time in seconds. Find the net angular displacement Δθ from the time t = 0 to t = 3 s. Also, find the number of revolutions N through which the gear turns during the 3s.
Ans: 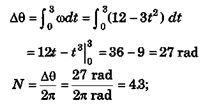
Δθ (2s) = 12 × 2 - 23 =16rad
θ3 - θ2 = 27 - 16 = 9 rad
So, in third second, N'=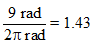
Ques 26: A solid body rotates about a stationary axis according to the law q = at - bt3, where a = 6 rad/s and b = 2 rad/s3. Find the mean values of the angular velocity and acceleration over the time interval between t = 0 and the time, when the body comes to rest.
Ans: 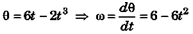
⇒ ω = 0 at t = 1s
∴ θ(0) = 0 and θ(1) = 6 - 2 = 4 rad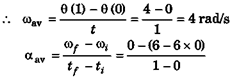
= -6 rad / s2
Angular Momentum
Ques 27: A particle of mass 1 kg is moving along a straight line y = x + 4. Both x and y are in metres. Velocity of the particle is 2 m/s. Find magnitude of angular momentum of the particle about origin.
Ans: 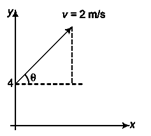
L = mv cos θ r, tan θ =dy/dx= 1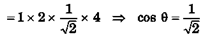
= 4√2 kg-m2/s
Ques 28: A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational axis.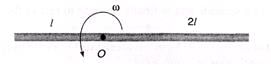
Ans: 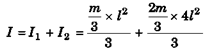
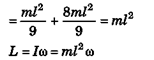
Ques 29: A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.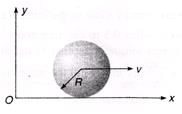
Ans: L = mvr + Iω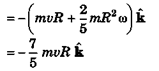
Ques 30: A rod of mass m and length 2R is fixed along the diameter of a ring of same mass m and radius R as shown in figure. The combined body is rolling without slipping along x-axis. Find the angular momentum about z-axis.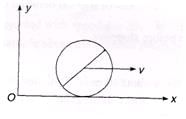
Ans: L = mvr + Iω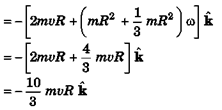
Conservation of Angular Momentum
Ques 31: If radius of earth is increased, without change in its mass, will the length of day increase, decrease or remain same?
Ans: As Iω = constant ⇒ T ∝ I.
With increase in R, I increases and so is T. So, length of day will increase.
Ques 32: The figure shows a thin ring of mass M = 1 kg and radius R = 0.4 m spinning about a vertical diameter. 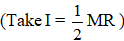 .
.
A small bead of mass m = 0.2 kg can slide without friction along the ring. When the bead is at the top of the ring, the angular velocity is 5 rad/s. What is the angular velocity when the bead slips halfway to θ = 45°.
Ans: I1ω1 = I2ω2
⇒ 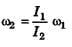
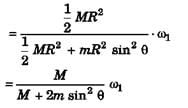
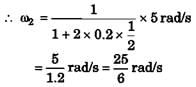
Ques 33: A horizontal disc rotating freely about a vertical axis makes 100 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis. If the number of revolutions per minute is thereby reduced to 90. Calculate the moment of inertia of disc.
Ans:
I1ω1 = (I1 + mr2)ω2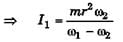
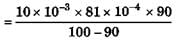
= 729 × 10-4 kg-m2
Q 34. A man stands at the centre of a circular platform holding his arms extended horizontally with 4 kg block in each hand. He is set rotating about a vertical axis at 0.5 rev/s. The moment of inertia of the man plus platform is 1.6 kg-m2, assumed constant. The blocks are 90 cm from the axis of rotation. He now pulls the blocks in toward his body until they are 15 cm from the axis of rotation.
Find (a) his new angular velocity and (b) the initial and final kinetic energy of the man and platform, (c) how much work must the man do to pull in the blocks ?
Ans: 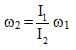
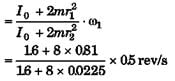
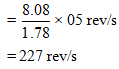
(b) 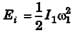
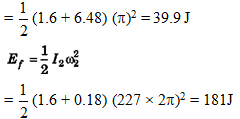
(c) ΔW = Ef -Ei = 181J - 39.9J = 141.1J
Ques 35: A horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body. Initially the body was located at the edge of the disc and the whole system rotated with an angular velocity w0. Then, by means of a force F applied to the lower end of the thread the body was slowly pulled to the rotation axis. Find:
(a) the angular velocity of the system in its final state,
(b) the work performed by the force F.
Ans:
(a) 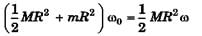
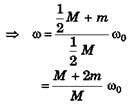
(b) 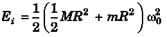
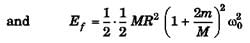
W = Ef - Ei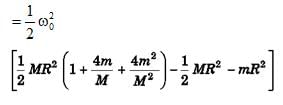
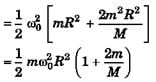
Pyre Rolling
Ques 36: Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point of contact. Calculate the acceleration of the cylinder and the frictional forces at the two contacts.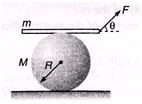
Ans: 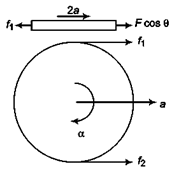
F cos θ - f1 = m.2a ...(i)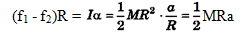
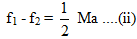
While, f1 + f2 = Ma ...(iii)
From Eqs. (ii) and (iii),
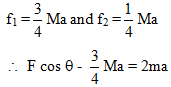

Ques 37: Find the acceleration of the cylinder of mass m and radius R and that of plank of mass M placed on smooth surface if pulled with a force F as shown in figure. Given that sufficient friction is present between cylinder and the plank surface to prevent sliding of cylinder.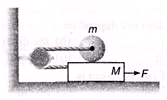
Ans: 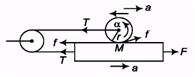
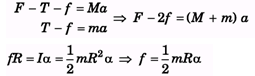
Ra - a = a ⇒ Rα = 2a ⇒ f = ma
∴ F - 2ma = (M + m) a ⇒ F = (M + 3m) a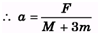
Ques 38: In the figure shown a force F is applied at the top of a disc of mass 4 kg and radius 0.25 m. Find maximum value of F for no slipping
Ans: 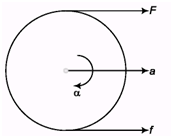
F + f = ma ...(i)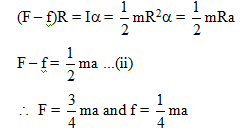
fmax = μmg = 1/4ma ⇒ a = 4μg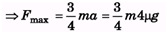
3μmg = 3 × 0.6 × 4 × 10 = 72N
Q 39. In the figure shown a solid sphere of mass 4 kg and radius 0.25 m is placed on a rough surface. Find : (g = 10 m/s2)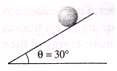
(a) minimum coefficient of friction for pure rolling to take place.
(b) If μ > μmin, find linear acceleration of sphere.
(c) If 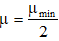 , find linear acceleration of cylinder. Here, μmin is the value obtained in part (a).
, find linear acceleration of cylinder. Here, μmin is the value obtained in part (a).
Ans: 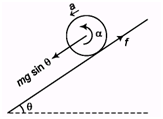
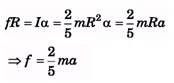
mg sin θ - f = ma ⇒ mg sin θ = 7/5 ma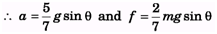
(a) For minimum value of μ,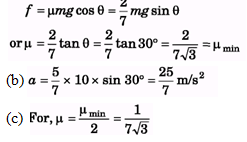
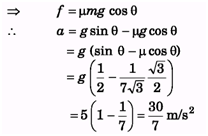
Angular Impulse
Ques 40: A uniform rod AB of length 2l and mass m is rotating in a horizontal plane about a vertical axis through A, with angular velocity ω, when the mid-point of the rod strikes a fixed nail and is brought immediately to rest. Find the impulse exerted by the nail.
Ans: 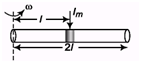
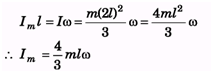
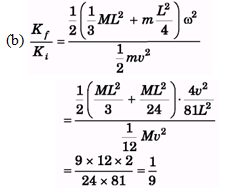
Ques 41: A uniform rod of length L rests on a frictionless horizontal surface. The rod is pivoted about a fixed frictionless axis at one end. The rod is initially at rest. A bullet travelling parallel to the horizontal surface and perpendicular to the rod with speed v strikes the rod at its centre and becomes embedded in it. The mass of the bullet is one-sixth the mass of the rod.
(a) What is the final angular velocity of the rod ?
(b) What is the ratio of the kinetic energy of the system after the collision to the kinetic energy of the bullet before the collision ?
Ans: 
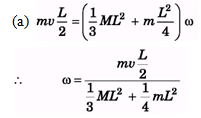
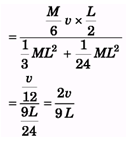
Ques 42: A uniform rod AB of mass 3m and length 2l is lying at rest on a smooth horizontal table with a smooth vertical axis through the end A. A particle of mass 2m moves with speed 2m across the table and strikes the rod at its mid-point C. If the impact is perfectly elastic. Find the speed of the particle after impact if:
(a) it strikes the rod normally,
(b) its path before impact was inclined at 60° to AC.
Ans: 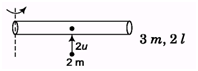
(a) 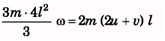
where, 2u= lω + v
⇒ v = -lω + 2u 4ml2
ω =2m(4u - lω)l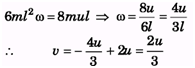
(b) 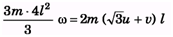
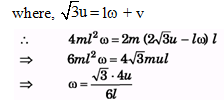
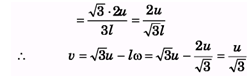
FAQs on DC Pandey Solutions (JEE Main): Mechanics of Rotational Motion- 1 - DC Pandey Solutions for JEE Physics
| 1. What are the basic principles of rotational motion? |  |
| 2. How is rotational motion different from linear motion? |  |
| 3. What is the importance of rotational motion in real-life applications? |  |
| 4. How is moment of inertia related to the distribution of mass in an object? |  |
| 5. How can the principles of rotational motion be applied to solve problems in physics? |  |





















