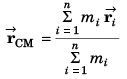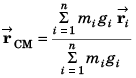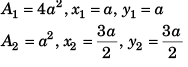DC Pandey Solutions: Centre of Mass, Conservation of Linear Momentum- 1 | DC Pandey Solutions for NEET Physics PDF Download
Introductory Exercise 8.1
Q.1. What is the difference between the centre of mass and the centre of gravity?
Ans. 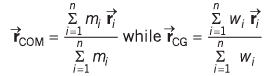
Here w = weight(mg) 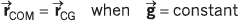
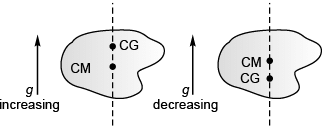
If a body is placed in a uniform gravitational field, the CG of the body coincides with the CM of the body.
while
If a body is placed in a uniformly increasing gravitational fieldin the upward direction the CG of the body will be higher level than the CM. And, if the body is placed in a uniformly decreasing gravitational field in the upward direction the CG will be at a lower level the CM.
CG shifts from CM according to the magnitude and direction of the gravitational field (by some other agency eg, earth) in which the body is placed.
In zero gravitational field CG has no meaning while CM still exists, as usual.
Q.2. The centre of mass of a rigid body always lies inside the body. Is this statement true or false?
Ans. False
The centre of mass of a rigid body may lie in side, on the surface and even out side the body. The CM of a solid uniform sphere is at its centre. The CM of a solid ring is at the centre of the ring which lies outside the mass of the body thus, the statement is false. (For further details see answer to 1 As sertion and Reason JEE corner)
Q.3. The centre of mass always lies on the axis of symmetry if it exists. Is this statement true or false?
Ans. True
The Centre of mass always lies on the axis of symmetry of the body, if it exists. The statement is thus true.
Q.4. If all the particles of a system lie in the y-z plane, the x-coordinate of the centre of mass will be zero. Is this statement true or false?
Ans. True.
Q.5. What can be said about the centre of mass of a solid hemisphere of radius r without making any calculation? Will its distance from the centre be more than r/2 or less than r/2?
Ans. less than r/2
As more mass is towards base.
Distance < r/4.
Q.6. All the particles of a body are situated at a distance R from the origin. The distance of the centre of mass of the body from the origin is also R. Is this statement true or false?
Ans. False
If two equal masses are kept at co-ordinates (R, 0) and ( - R, 0), then their centre of mass will lie at origin.
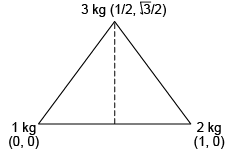
Q.7. Three particles of mass 1 kg, 2 kg and 3 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Find the distance of their centre of mass from A.
Ans. 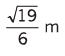
= Distance of centre of mass from A
Q.8. Find the distance of centre of mass of a uniform plate having semicircular inner and outer boundaries of radii a and b from the centre O.
Hint: Distance of COM of semicircular plate from centre is 
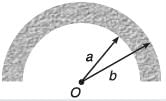
Ans. 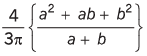
Q.9. Find the position of centre of mass of the section shown in figure.
Note- Solve the problem by using both the formulae: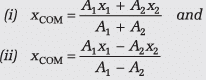
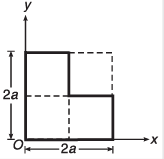
Ans.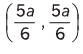
FAQs on DC Pandey Solutions: Centre of Mass, Conservation of Linear Momentum- 1 - DC Pandey Solutions for NEET Physics
| 1. What is the concept of centre of mass? |  |
| 2. How is the centre of mass calculated? |  |
| 3. What is conservation of linear momentum? |  |
| 4. How is linear momentum calculated? |  |
| 5. How is the centre of mass related to the conservation of linear momentum? |  |