Important Calorimetry & Heat Transfer Formulas for JEE and NEET
1. Calorimetry
(i) Q = msΔθ = cΔθ, when temperature changes without change in state.
(ii) Q = mL, when state changes without change in temperature.
(iii) s = specific heat of any substance
= heat required to increase the temperature of unit mass by 1°C or 1 K.
(iv) c = heat capacity of a body = ms
= heat required to increase the temperature of whole body by 1°C or 1 K.
(v) Specific heat of water is 1 cal g-1 - °C between, 14.5°C and 15.5°C.
(vi) L = latent heat of any substance
= heat required to convert unit mass of that substance from one state to another state.
(vii) Water equivalent of a vessel It is mass of equivalent water which takes same amount of heat as taken by the vessel for same rise of temperature.
2. Heat Transfer
Heat conduction through a rod
(i) Heat flow in steady state 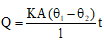
(ii) Rate of flow of heat = heat current or 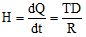
Here, TD = temperature difference = θ1 - θ2 and R = thermal resistance = 1/KA
Radiation
(i) Absorptive power, a= 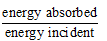
a ≤ 1
a = 1 for perfectly black body.
(ii) Spectral absorptive power al = absorptive power of wavelength l.
al ≤ 1
al = 1 for perfectly black body.
(iii) Emissive power e Energy radiated per unit area per unit time is called emissive power of a body. Its SI units are Js-1m-2 or Wm-2.
(iv) Spectral emissive power el Emissive power of wavelength l is known as spectral emissive power.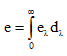
(v) Stefan's law Emissive power of a body is given by,
e = erσT4
Here er = emissivity, emittance, relative emissivity or relative emittance.
er ≤ 1
er = 1 for a perfectly black body.
Sometimes emissivity is also denoted bye. In that case differentiate them by their units. er is unitless while e has the units Wm-2.
(vi) Total energy radiated by a body,
E = erσT4 At
Here, A = surface area and t = time.
(vii) a = er or absorptivity of a body = its emissivity.
(viii) Kirchhoff s law If different bodies (including a perfectly black body) are kept at same temperatures, then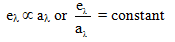
or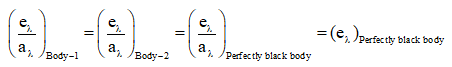
From this law following two conclusions can be drawn.
(a) Good absorbers of a particular wavelengthare also good emitters of same wavelength l.(b) At a given temperature, ratio of ql and al for any body is constant. This ratio is equal to el of perfectly black body at that temperature.
(ix) Wien's displacement law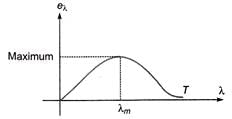
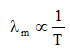
or
λmT = Constant
= Wien's constant b Here, b = 2.89 × 10-3 m-K
Further, area of this graph will give total emissive power which is proportional to T4,
(x) Cooling of a body by radiation
(a) Rate of cooling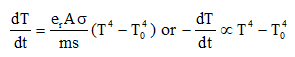
(b) Newton's law of cooling If temperature difference of a body with atmosphere is small, then rate of cooling µ temperature difference.
(c) If body cools by radiation according to Newton, then temperature of body decreases exponentially.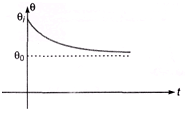
In the figure,
θI = initial temperature of body
θ0 = temperature of atmosphere.
Temperature at any time t can be written as, θ = θ0 + (θI - θ0)e-αt
(d) If body is cooling according to Newton then to find temperature of a body at any time t, we will have to calculate e-αt. To avoid this, you can use a shortcut approximate formula given below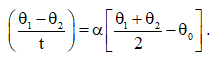
|
97 videos|379 docs|103 tests
|

















